
机器学习基础教程:神经网络
在之前的文章中,我通过展示学习过程中成本函数和梯度下降的核心作用,阐述了机器学习的工作原理。本文以此为基础,探索神经网络和深度学习如何工作。这篇文章重点在于解释和编码。原因是我想不出有什么方法可以比3bule1brown做的视频更清楚地阐明一个神经网络的内部工作原理。
链接:
什么是神经网络?
如何学习神经网络?
反向传播到底做了什么?
反向传播演算:深学习章节附录
通过简单的线性回归理解机器学习的基本原理
这些视频显示神经网络如何输入原始数据(如数字图像),并能以惊人的准确性输出这些图像的标签。这些视频以一种非常容易理解的方式突出了神经网络的基础数学运算,即使那些没有很深数学背景的人也可以开始理解深度学习的内部原理。

本文旨在为这些视频的做“code-along”的补充(完整的Tensorflow和Keras脚本文末提供)。目的是演示如何在Tensorflow中定义和执行神经网络,例如如何能够识别如上所示的数字。
TensorFlow是Google的深度学习库,虽然它是相当低级(我通常使用更高级别的Keras库来进行深度学习),但我认为这是一个很好的学习方式。这仅仅是因为,虽然在幕后做了很多不可思议的事情,但它需要你明确定义神经网络的架构。这样做,你会更好地了解它的工作原理。
定义图层和激活
在第一步中,我们为网络定义架构。我们创建一个由一个输入层,两个隐藏层和一个输出层组成的四层网络。请注意,来自一个层的输出是如何输入到下一层的。就神经网络而言,这个模型非常简单,它由密集或完连接层组成,但是仍然非常强大。
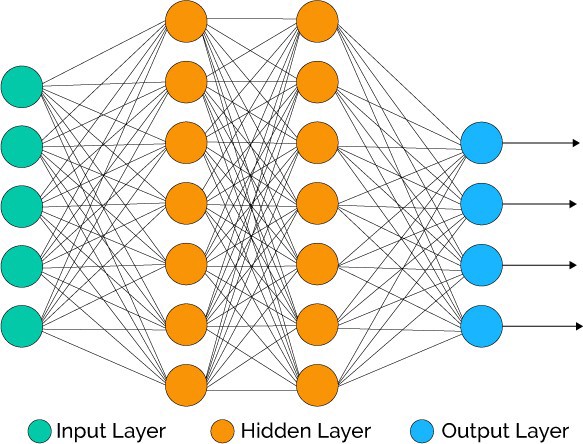
输入层 -有时也被称为可见层(visible layer ),是模型中表示数据原始状态的层。例如,对于数字分类任务,可见层由对应于像素值的数字表示。
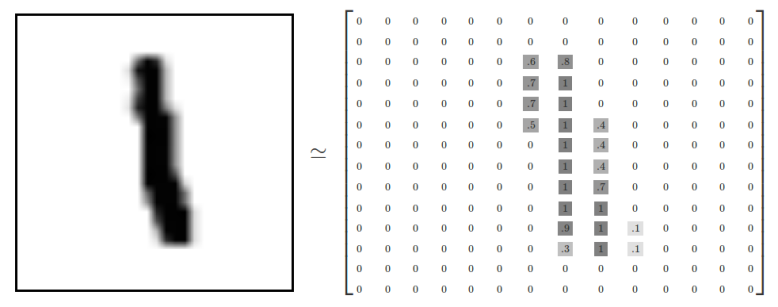
在TensorFlow中,我们需要创建一个占位符变量来表示这个输入数据,我们还将为每个输入对应的正确标签创建一个占位符变量。这样就建立了训练数据,我们以此训练神经网络的X值和y值。
隐藏层使神经网络能够创建的模型用于学习数据和标签之间复杂的抽象关系的输入数据的新表示。隐藏层由神经元组成,每个神经元代表一个标量值。这个标量值被用来计算输入加偏置的权重和(本质上是y1 ~ wX + b),创建一个线性(或者说仿射)变换。
在Tensorflow中,你必须明确定义组成该层的权重和偏置的变量。我们通过将它们包装在tf.Variable函数中来实现,因为参数将随着模型学习最能表示数据中的关系的权重和偏置而更新,所以这些函数要被包装为变量。我们使用方差非常低的随机值来实例化权重,并用零填充偏置变量。然后我们定义在层中发生的矩阵乘法。
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import begin
l1_nodes = 200
l2_nodes = 100
final_layer_nodes = 10
# define placeholder for data
# also considered as the "visibale layer, the layer that we see"
X = tf.placeholder(dtype=tf.float32, shape=[None, 784])
# placeholder for correct labels
Y_ = tf.placeholder(dtype=tf.float32)
# define weights / layers here
# needs weights and bias for each layer in the network. Input to one layer is the
# output from the previous layer
w1 = tf.Variable(initial_value=tf.truncated_normal([784, l1_nodes], stddev=0.1))
b1 = tf.Variable(initial_value=tf.zeros([l1_nodes]))
Y1 = tf.nn.relu(tf.matmul(X, w1) + b1)
w2 = tf.Variable(initial_value=tf.truncated_normal([l1_nodes, l2_nodes], stddev=0.1))
b2 = tf.Variable(tf.zeros([l2_nodes]))
Y2 = tf.nn.relu(tf.matmul(Y1, w2) + b2)
w3 = tf.Variable(initial_value=tf.truncated_normal([l2_nodes, final_layer_nodes], stddev=0.1))
b3 = tf.Variable(tf.zeros([final_layer_nodes]))
Y = tf.nn.softmax(tf.matmul(Y2, w3) + b3)
# defien cost function and evaluation metric
cross_entropy = -tf.reduce_sum(Y_ * tf.log(Y))
is_correct = tf.equal(tf.argmax(Y, 1), tf.argmax(Y_, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
# gradient descent
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.003)
train_step = optimizer.minimize(loss=cross_entropy)
然后通过一个激活函数(这里我使用的是ReLU)传递这个变换,使线性变换的输出变成非线性。这使得神经网络可以对输入和输出之间的复杂非线性关系进行建模。
输出层是模型中的最后一层,在本例中为每个标签的一个节点,大小为10。我们将softmax激活应用在这个层,以便在最后的层的节点中输出介于0和1之间的值,以表示标签的可能性。
成本函数和优化
现在神经网络结构定义完成,我们设置了成本函数和优化器。对于这个任务我使用分类交叉熵。我还定义了一个可用于评估模型性能的准确性度量。最后,我将优化器设置为随机梯度下降,并在实例化后调用其最小化方法。
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(1000):
batch_X, batch_y = mnist.train.next_batch(100)
# associate data with placeholders
train_data = {X: batch_X, Y_: batch_y}
# train model
sess.run(train_step, feed_dict=train_data)
# capture accuracy and loss metrics
train_a, train_c = sess.run([accuracy, cross_entropy], feed_dict=train_data)
# measure performance on test data
test_data = {X: mnist.test.images, Y_: mnist.test.labels}
test_a, test_c = sess.run([accuracy, cross_entropy], feed_dict=test_data)
if i % 100 == 0:
print("accuracy on test data is {}".format(train_a))
最后,模型可以运行(在这里迭代1000次)。在每一次迭代中,将一小部分数据输入到模型中,进行预测,计算损失并通过反向传播,更新权重然后重复此过程。
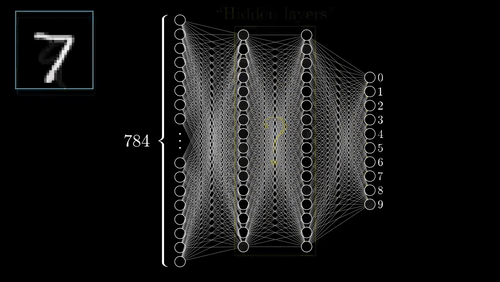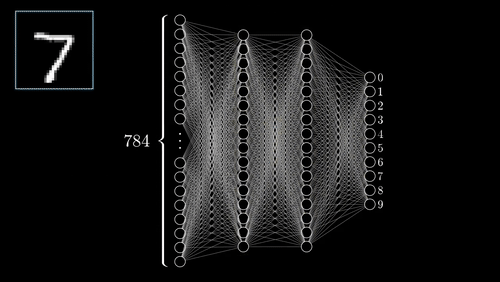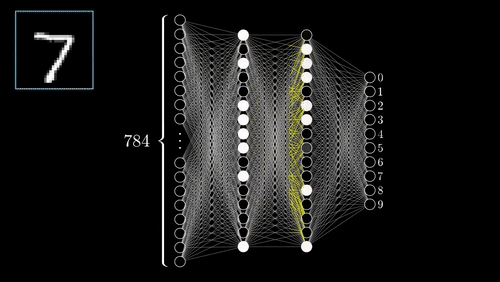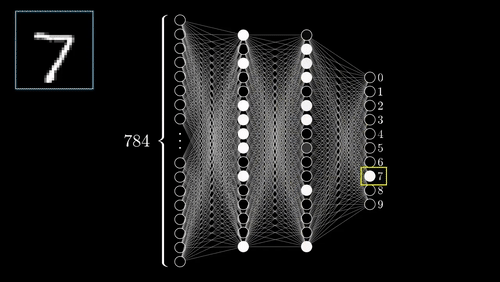
这个简单的模型在测试集上的准确性达到了95.5%左右。在下面的图中,你可以看到模型每次迭代的准确性和成本,训练集的性能和测试集的性能显然存在差异。
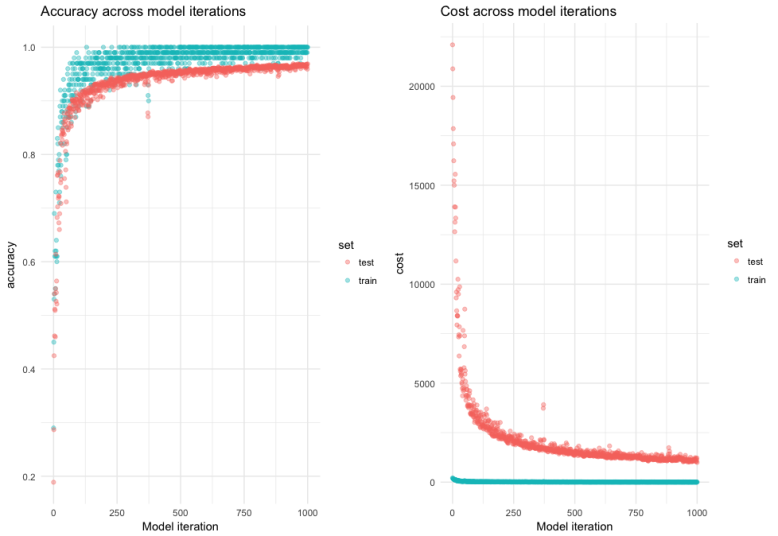
这是过拟合的表现。也就是说,该模型能很好地学习训练数据,但这限制了它的一般性。我下一篇文章的文章会讲到如何处理。
Tensorflow:https://gist.github.com/conormm/1c82b093c9c6002e7ca6ff6e9fb34f05
Keras:https://gist.github.com/conormm/e1dd2ee37733f4817e09a41d625d9e7f
































