赫尔辛基大学AI基础教程:赔率和概率(3.1节)
从信息的缺失到故意的欺骗,现实世界有许多未知的可能性。
以自驾车为例:你可以设定目标,遵循交通法规以有效和安全的方式从A驾驶到B。但是如果交通情况比预期的更糟,可能发生什么?也许是因为前面发生了事故?突然恶劣的天气?随机事件就像在街上弹跳的球?或者是一片直接飞进汽车摄像头的垃圾?

自驾车需要使用各种传感器,包括类似声纳的传感器和相机,来检测它的位置和周围的情况。这些传感器从来都不是完美的,因为来自传感器的数据总是包含一些称为“噪声”的错误和不准确性。这是非常普遍的,比如一个传感器指示前方的道路左转,但另一个传感器指示相反的方向。在必须解决这个问题的时,不能只有一点点的噪音就要停车解决。
概率
现代人工智能方法实际上会在现实世界问题中起作用的原因之一就是,与1960年代至1980年代早期的大多数“老式”方法不同,他们有处理不确定性的能力。
注:
处理不确定性的历史
人工智能的历史经历了各种各样的处理不确定和不精确信息的竞争范式。例如,你可能听说过模糊逻辑。模糊逻辑有一段时间是处理不确定和不精确信息的最佳方法之一,并且在许多客户应用中使用,例如洗衣机,机器可以检测到污垢(会给出程度,而不是脏还是干净的简单判断),并且以此调整程序。
然而,在不确定性情况下,概率已成为不确定性推理的最佳方法,几乎所有当前的AI应用都至少在一定程度上基于概率。

为什么概率很重要
在游戏中,我们可能最常见概率的应用:在扑克中出现三条的机会有多大(约46分之一),彩票赢钱的机会有多大(特别小)等等。然而,更重要的是,概率也可以用来量化和比较日常生活中的风险:如果超出限制速度,汽车撞车的可能性有多大?你抵押贷款利率在未来五年内会上升5个百分点的可能性有多大?或者AI会自动执行特定任务,例如在x射线照片中检测骨折的骨头,或者在餐馆里做侍应生的可能性有多大。
注:
关于概率重点要学到什么
我们希望你学到的关于概率的最重要的东西不是概率微积分。相反,这是将不确定性看作一种可以量化的(至少在原则上可以量化的)事物的能力。也就是说我们可以把不确定性当作一个数字来讨论:数字可以进行比较(“这件事情比这件事更有可能”),并且它们通常可以被测量。概率的数字有时会有点主观,但我们仍然可以精确地评估它们,尽管有时我们的数字会被发现可能不对。换句话说,你要学到的是不确定性不在理性思考和讨论的范围之内的东西。
不确定性可以被量化的事实价值重大。举个例子,关于疫苗接种或其他公共政策的决定。在进入市场之前,任何疫苗都经过临床测试,因此其效益和风险已经量化。我们不知道这些风险的细节,但它们的大小通常足以说明好处是否超过风险。
注:
为什么要量化不确定性问题
如果我们把不确定性看作是无法量化或测量的东西,那么不确定性可能成为理性讨论的障碍。例如,我们可能会争辩说,由于我们不确切知道疫苗是否会造成有害的副作用,因此使用太危险。但是,这可能会导致我们忽视疫苗将消灭威胁生命的疾病。在大多数情况下,已知的好处和风险具有足够的精确度,以清楚地看到哪个更重要。
以上的经验在许多日常情景和职业中都很有用:例如,医生,法官,投资者必须处理不确定的信息并根据这些信息作出合理的决定。由于这是一个AI课程,我们将讨论如何使用概率来自动化不确定推理。我们将使用的示例包括医疗诊断(尽管它通常不是我们希望自动化的任务),和识别欺诈性电子邮件(“垃圾邮件”)。
练习8:概率预测
思考以下四个概率预测和结果。根据预测结果的正确性可以得出什么结论?我们能否得出推断:预测给出的概率确实是正确的(选择“对”),预测是错误的(选择“错”),或者无法得出结论(选择“不能得出结论”)。
1.天气预报称,明天天气将以90%的概率下雨,但全天都是晴。
2.天气预报称,明天天气将以0%的概率下雨,但这天下雨了。
3.假设你长时间监视天气预报员。你只统计预测会有70%的降雨机率的日子。你发现从长远来看,这些日子平均每五天就有三天下雨。
4.在2016年美国总统大选中,一个著名的政治预测博客Five-Thomson认为希拉里·克林顿的胜率为71.4%(vs特朗普的28.6%)。然而,与预测相反,唐纳德·特朗普当选为第45任美国总统。
赔率
赔率可能是代表不确定性的最简单方法。当有更多信息可用时,它特别容易更新信念(我们将在下一节讨论这一点)。
在我们继续进行之前,我们应该确保你熟悉对比例(或者说分数)的基本操作。你应该记得,分数是像3/4或21/365这样的数字。我们需要对这些东西进行乘法和除法,所以如果你对忘记了这些,那么可以访问(https://en.wikibooks.org/wiki/Arithmetic/Multiplying_Fractions)。或者访问(https://www.mathsisfun.com/algebra/rational-numbers-operations.html)查看操作的动画演示。
使用赔率计算,例如3:1(读作三比一),这意味着每三个我们期望的结果,例如赢下一个赌注,就会有一个结果相反的结果(即输掉赌注)。换句话说获胜的几率是3/4。这些被称为固有频率,因为它们只涉及整数。使用整数,有利于我们想象,例如,四个人中有三个棕色眼睛。或者一连四天,三天下雨(在赫尔辛基就这样)。

注:
为什么我们使用赔率而不是百分比
四分之三当然与75%相同(数学家倾向于使用0.75这样的分数而不是百分比)。我们发现,人们在处理分数和百分比时比处理自然频率或者说赔率更容易产生混淆和错误。所以我们在方便的时候使用自然频率和赔率。
需要注意的重要一点是,虽然表示为两个数字,例如3和1,但其实际可能被认为是单个分数或比值,例如3/1。因此赔率3:1与赔率6:2或30:10相同,因为它们也等于3/1。同样,赔率1:5等于1/5 = 0.2,这与赔率2:10或10:50相同。但你要小心:赔率1:5,即使它可以表示为0.2,但也不同于概率的20%(概率的0.2)。对于大于1的赔率,如5:1,很容易记住,因为概率不可能大于1(或大于100%),但是对于小于1的概率如1:5,就很容易混淆。下面的练习将进一步说明赔率和概率之间的对应关系。
练习9:赔率
如上所述,赔率3:1等于概率的0.75(或百分比75%)。
一般来说,如果赞成事件的赔率是x:y,则事件的概率等于x /(x + y)。
正如我们前文说的那样,6:2的概率等于和3:1完全相同的概率,因为对于x = 6和y = 2,我们得到相同的结果:x /(x + y)= 6 /(6 + 2)= 6 / 8 = 3/4 = 0.75。
你的任务:
对于前三题1-3,从赔率转换为整数的比值; 例如从1:1到1/2。
对于后三题4-6,将概率转换为百分比(例如4.2%)。以百分比形式给出答案,取一位小数,例如12.2%。
提示:计算要用一个简单的计算器,公式可以在上面找到。
1.在扑克中获得三条机会大概是1:46。
2.赫尔辛基下雨的可能性为206:159。
3.圣地亚哥的降雨可能性为23:342。
4.在扑克中获得三条机会大概是1:46。
5.赫尔辛基下雨的可能性为206:159。
6.圣地亚哥的降雨可能性为23:342。
练习7:Max为何悲观?
让我们回到本节开头描述的井字棋。为了缩小可能的最终游戏空间,我们可以观察到,Max必须明确地将X放在第一排以避免即将到来的失败:
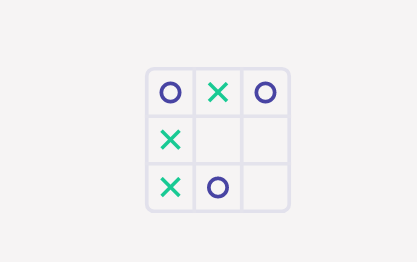
现在轮到Min画O。使用Minimax算法以此为根,评估在这种游戏状态下的值以及游戏树中的其他状态。
你的任务:
看看从下面棋盘位置开始的游戏树。用笔和纸填写游戏结束时底层节点的值。请注意,这次有些游戏以平局结束,这意味着节点的值是0。
接下来继续填充倒数第二级节点的值。由于这级没有分支,与底层的值相同。
在倒数第三级,通过为每个节点选择子节点的最大值来填充值 - 如你所见,这是一个MAX级。最后,通过选择根节点的子节点值的最小值来填充根节点的值。这就是游戏的值。
输入游戏的值作为答案。
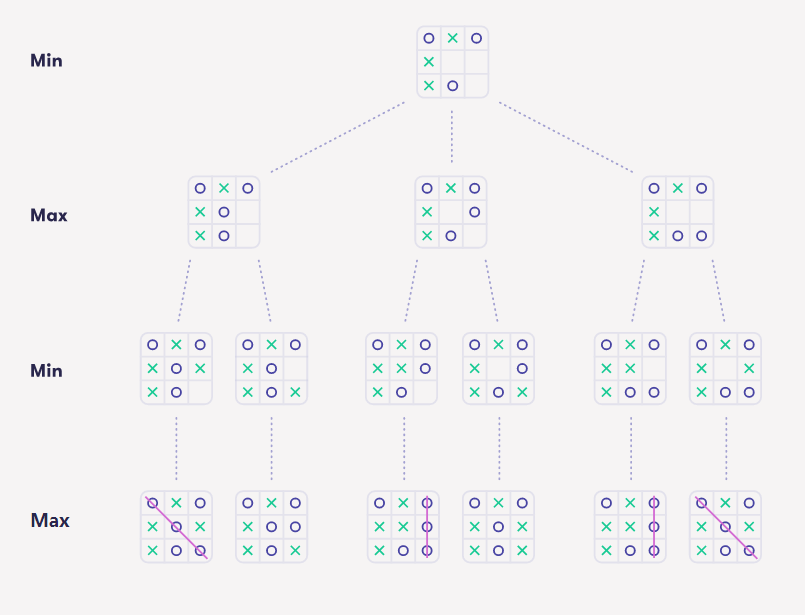
答案: -1
值是-1。第二级上的值是0,0和-1。第三级上的值是-1,0,-1,0,-1,-1,与底层上的值相同。如你所见,Max之所以悲观是由于在右下角(节点(4)),Min可以选择节点4来确保胜利。Min一定能赢,所以值为-1。
赫尔辛基大学AI基础教程合集:赫尔辛基大学AI基础教程































