深度学习不只是“Import Tensorflow”(上)
2019年11月23日 由 sunlei 发表
88565
0
如今,像Pytorch和TensorFlow这样的工具使得人工智能的开发变得如此简单,以至于许多该领域的新手甚至都懒得去学习神经网络是如何工作的。
当这样的对话正在发生的时候,我真希望我是在夸大其辞——
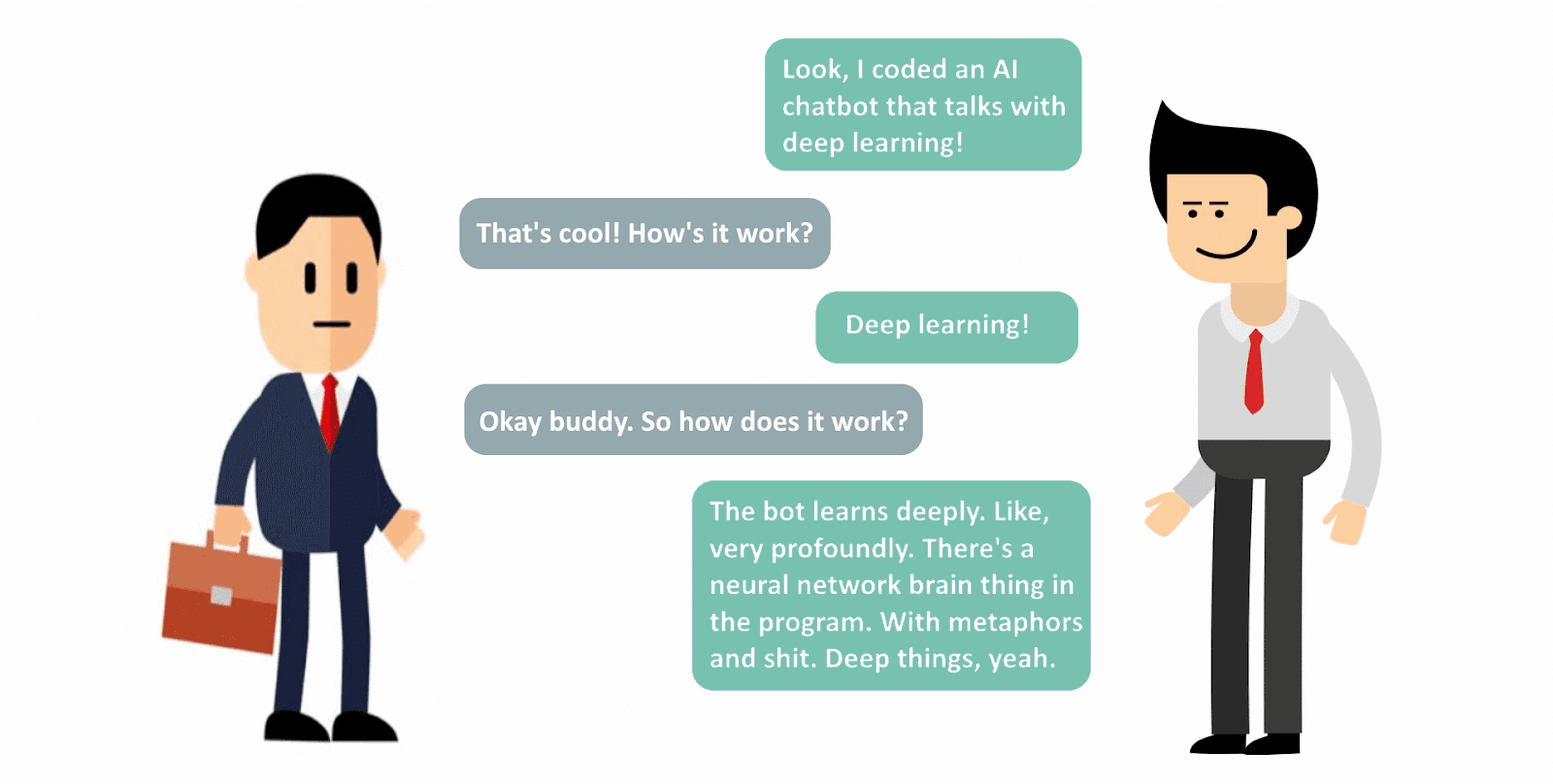
显然,这是个问题。如果你刚接触人工智能,不要做右边那个人。它给你和我一个坏名声。但更重要的是,当你“使用深度学习”时,你要理解工作中的算法。
Deep Learning Explained in 7 Steps
这样,您可以为正确的任务选择正确的模型,当您遇到问题时,您知道如何修复它们。
事实是,如果你在人工智能领域工作,你不会每次创建一个神经网络时都用手工编码。如果你研究一下人工智能在现实世界中的应用——比如YouTube的推荐系统或SnapChat的换脸过滤器——像TensorFlow和Pytorch这样的库是很常见的。
这是因为这些库是复杂的、易于使用的和高效的。
 但是即使这样,如果您不了解它们是如何工作的,您也不会了解太多。你将无法开发自己的深度学习算法或模型,你也不知道如何调整或改进现有的算法或模型。
但是即使这样,如果您不了解它们是如何工作的,您也不会了解太多。你将无法开发自己的深度学习算法或模型,你也不知道如何调整或改进现有的算法或模型。
那么深度学习是如何起作用的呢?
不是作为一种灵活的方式来导入库,而是作为一个数学概念?
好了,系好安全带,兄弟,我们要潜下去了。
虽然人工智能在20世纪50年代到80年代一直是科学家们的热门话题,但这个行业直到最近20年才开始席卷全球。
它最近的普及可以归功于多伦多大学(University of Toronto)教授杰弗里•辛顿(Geoffrey Hinton)在深度学习方面取得的突破,以及世界上计算能力和可用数据量的指数级增长。
[caption id="attachment_47139" align="aligncenter" width="1200"] 杰弗里·辛顿,被誉为“深度学习的教父”。图片来源于多伦多生活。[/caption]
杰弗里·辛顿,被誉为“深度学习的教父”。图片来源于多伦多生活。[/caption]
深度学习是人工智能的一个子集,它使用的算法模仿人类大脑,称为神经网络。
深度学习、更好的硬件和更多的数据的出现,使得以前不可想象的技术得以发展。其中包括实时目标检测和分类算法、自动驾驶汽车、股市预测模型、生成设计软件等等。
本质上,神经网络学习输入变量和输出变量之间的关系。给定一组x和y的足够数据,神经网络学习准确地从x映射到y。
神经网络由相互连接的处理单元层组成。这些元素被称为“节点”或“神经元”,它们一起工作来解决复杂的问题。节点被组织成层,层又分为三种主要类型:输入层、隐藏层和输出层。
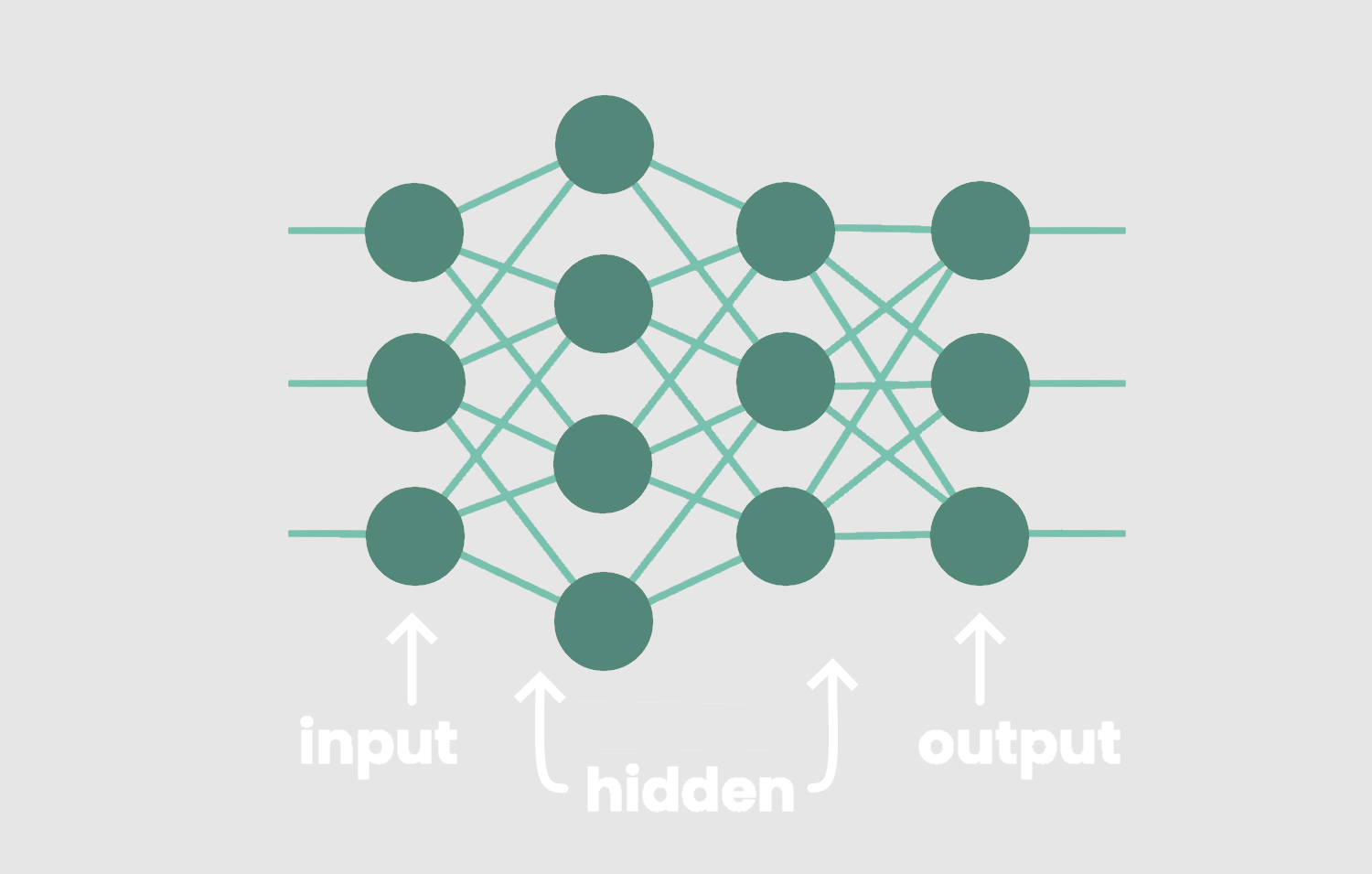
输入层的节点接收输入值,隐藏层的节点执行隐藏计算,输出层的节点返回网络的预测。
假设我们正在训练我们的网络来识别16x16像素网格中的手写数字。为了接收来自该图像的输入,我们将为输入层分配16x16或256个节点。从图像的左上角开始,每个像素由一个节点表示。
[caption id="attachment_47141" align="aligncenter" width="1439"] 每个像素对应一个输入节点。[/caption]
每个像素对应一个输入节点。[/caption]
输入节点将包含-1和1之间的某个数值,以表示其对应像素的亮度,其中-1是深色,1是白的。
当这些值被输入到网络中时,它们就从一个神经元层向前传播到下一个神经元层。
[caption id="attachment_47142" align="aligncenter" width="998"]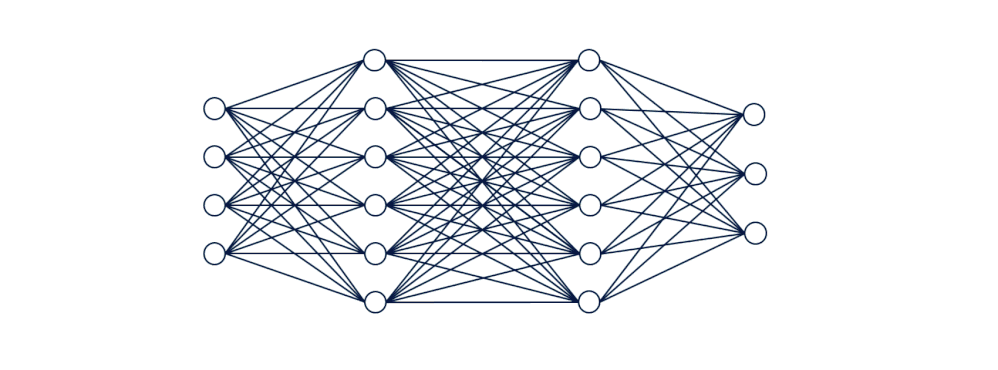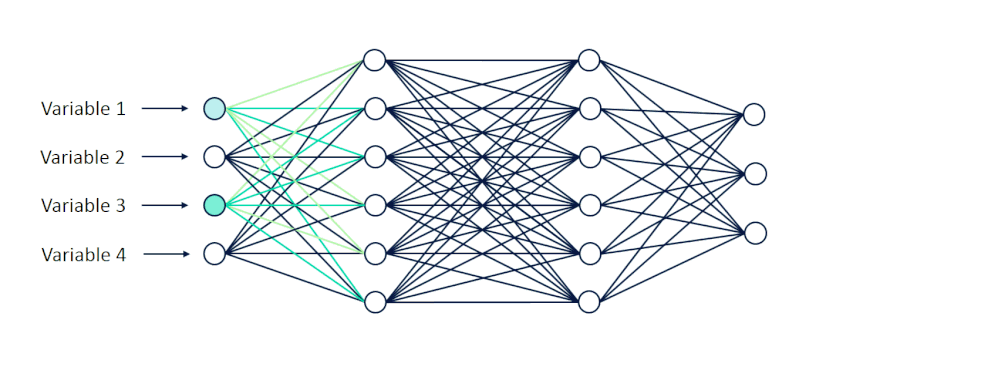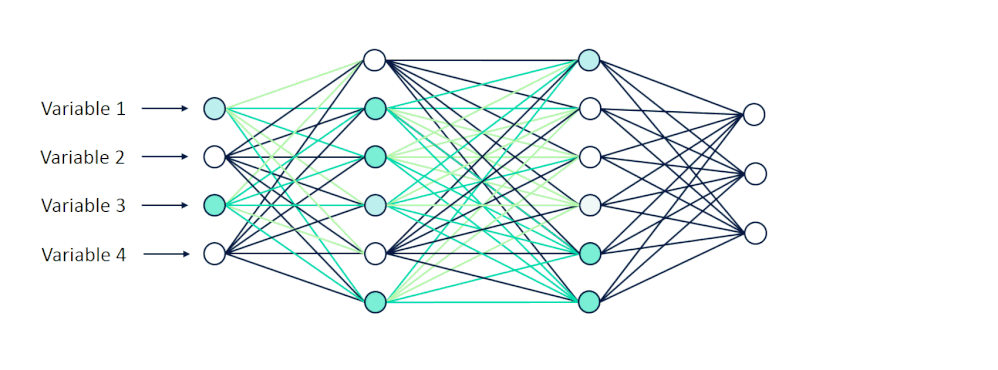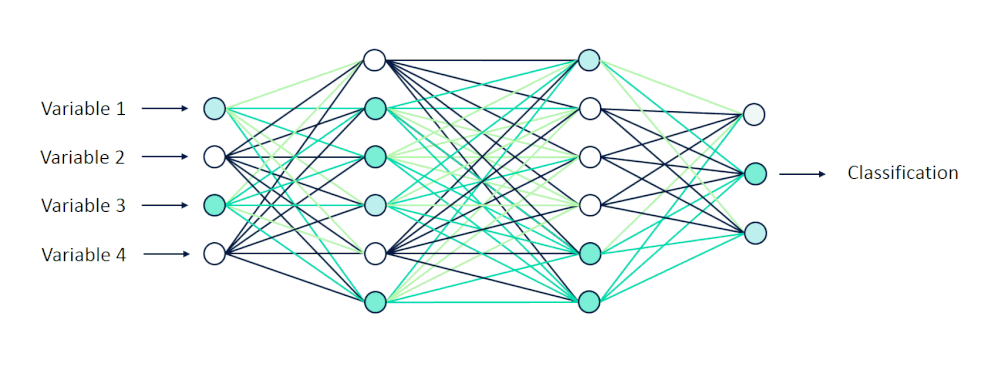 可视化向前传播[/caption]
可视化向前传播[/caption]
在它们通过隐藏层中的一系列计算之后,我们期望接收10个输出,其中每个输出节点表示0到9之间的一位数字。
假设,如果我们向网络显示一个手写的“4”,那么网络应该将我们的图像分类为“4”。在数学上,与数字“4”对应的节点将返回输出层中的最高值。
总之,输入层的节点接收输入值,隐藏层的节点执行计算,输出层的节点返回预测。
最大的问题是,我们的神经网络如何建立关系模型?为了理解神经网络的工作原理,我们必须首先理解隐藏层中单个节点的功能。我们可以将单个节点的功能与统计学中的一个标志性模型——线性回归的功能进行比较。
线性回归可以定义为对线性关系进行建模的一种尝试。
假设你有一组包含两个定量变量的数据:

如果你将学生的分数与他们在散点图中学习的小时数进行比较,你会发现一个正的线性关系。

一般来说,学生花在学习上的时间越长,他们在考试中取得高分的可能性就越大。线性回归试图做的是通过在散点图上画一条最合适的直线来模拟这种线性关系,我们称之为线性模型。
线性模型基本上是一条直线,y = mx + b,它通过尽可能多的数据。
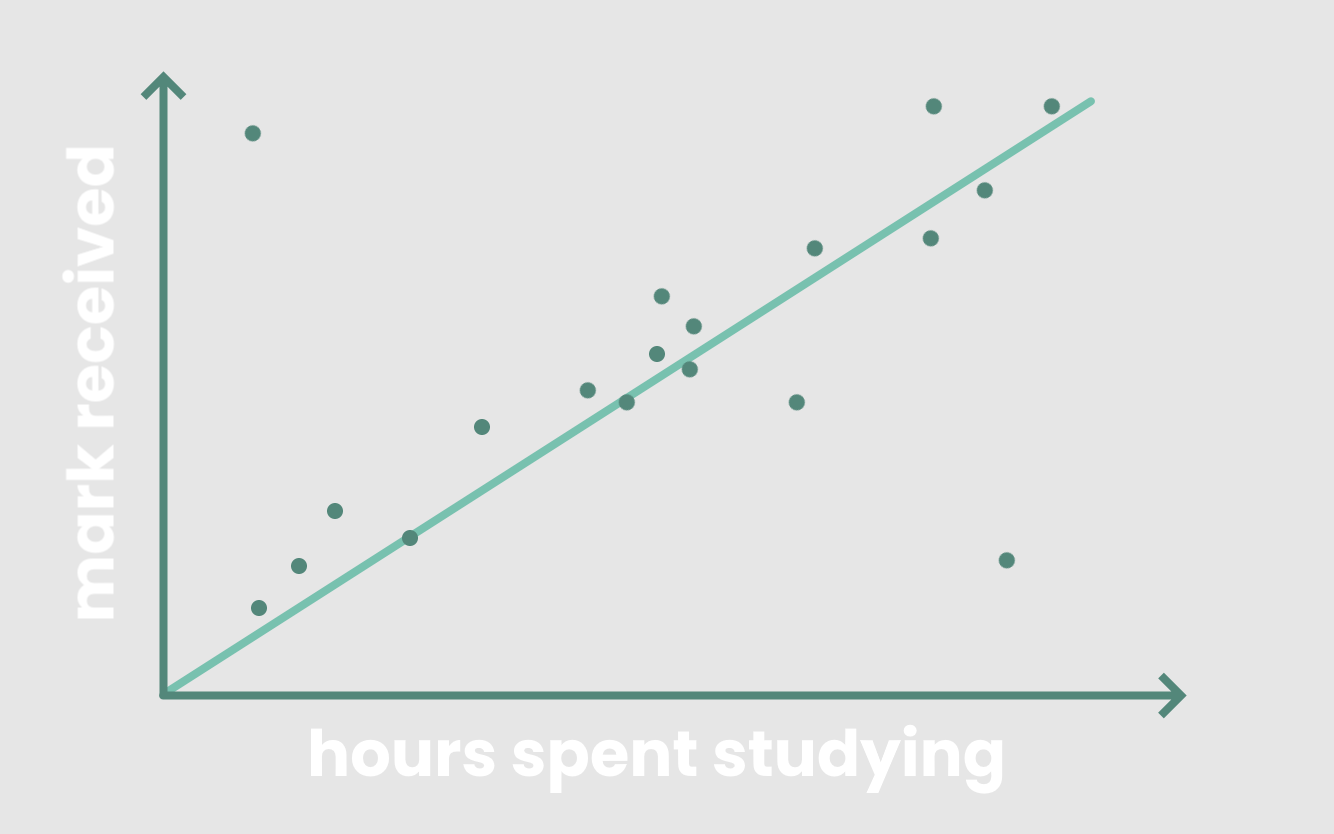
理想的线性模型应该是最小化学生实际分数与模型预测分数之间的误差,或者最小化模型实际y值与预测y值之间的误差。
让我们仔细看看数学。
在线性模型中,输入x乘以常数m,然后加上输入b,称为“截距”。这些输入相加得到输出y。
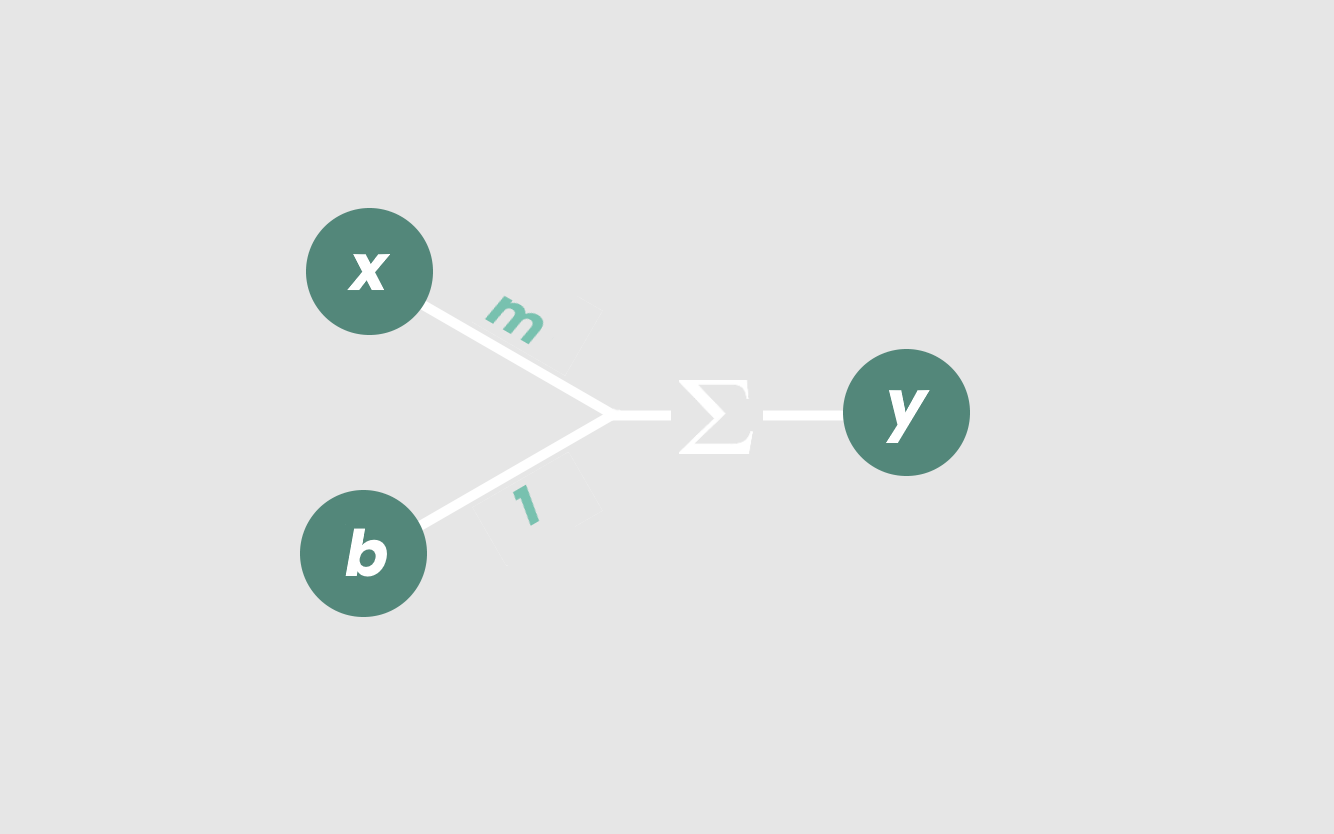
得到的直线y = mx + b模拟了x和y之间的关系。
如果我们要修改输入的值,我们需要一条不同的线。例如,将常数b从2变为3意味着将直线向上平移,使其与y轴相交的位置是y = 3而不是y = 2。
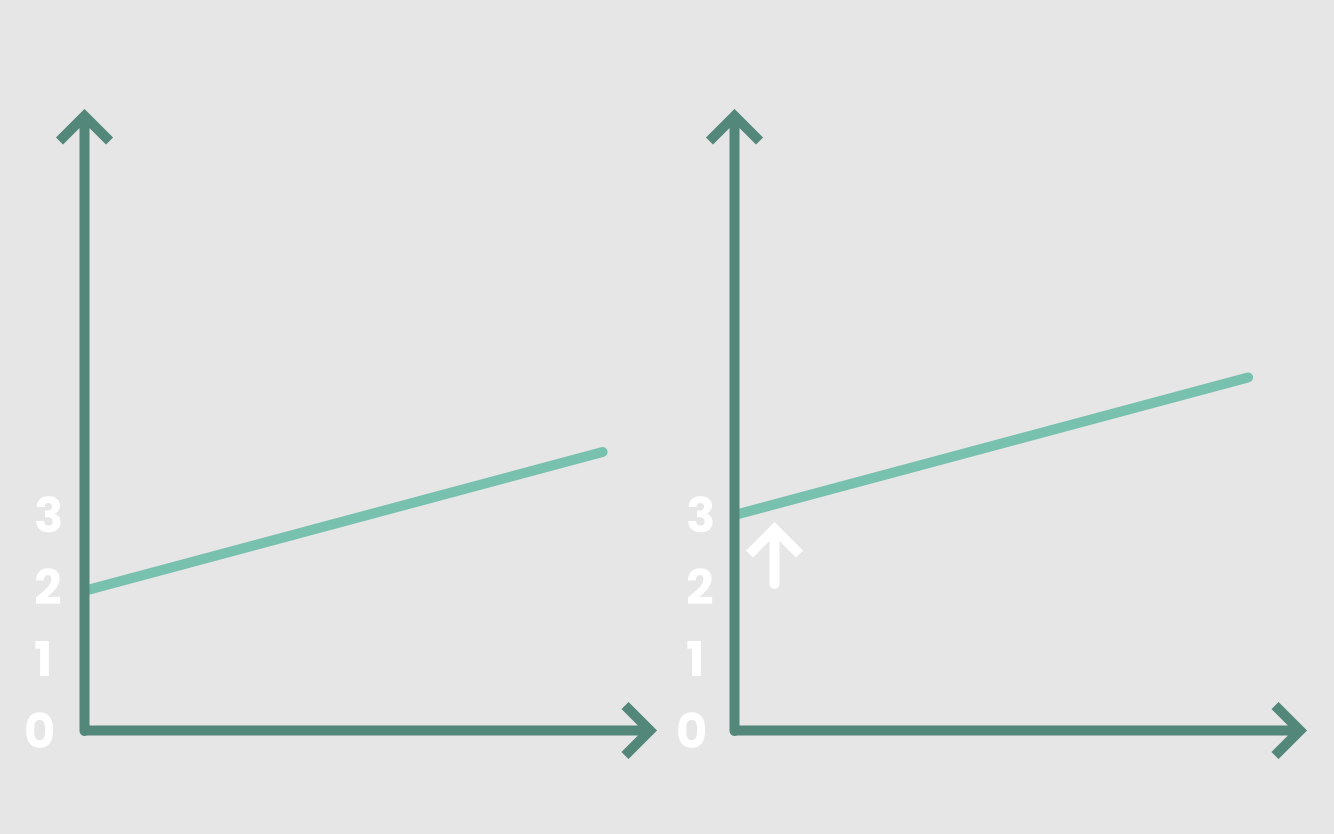
我花这么长时间和你一起复习九年级的数学,原因很简单。单个神经元的工作方式完全相同!
在神经元中,输入x₁乘以一个重量,w₁。在我们输入x₁乘以w₁,我们称之为“加权输入”。
然后添加一个常数b₁-它的行为类似于线性模型中的y截距,称为“偏差”。然后将加权输入和偏差相加得到我们的输出,v₀。
[caption id="attachment_47148" align="aligncenter" width="1334"]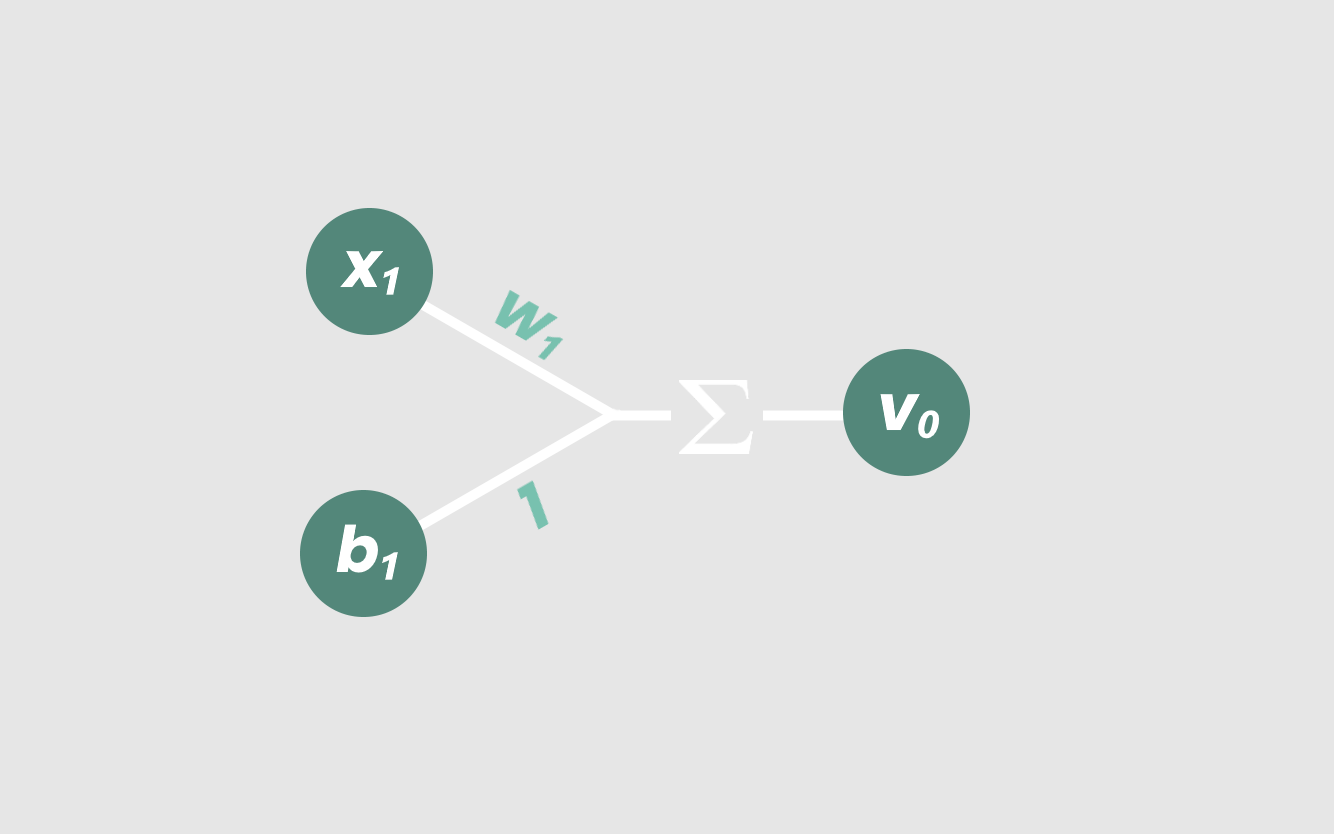 看起来很眼熟,不是吗?[/caption]
看起来很眼熟,不是吗?[/caption]
好了!一个基本的神经元。
再次,我们可以通过调整权重w₁或偏差b₁来调整v₀的值。如果我们修改这两个参数中的任何一个,我们将再次期望看到一个不同的线性模型。
原文链接:https://medium.com/datadriveninvestor/deep-learning-is-not-just-import-tensorflow-c27136aaa65e
当这样的对话正在发生的时候,我真希望我是在夸大其辞——

显然,这是个问题。如果你刚接触人工智能,不要做右边那个人。它给你和我一个坏名声。但更重要的是,当你“使用深度学习”时,你要理解工作中的算法。
Deep Learning Explained in 7 Steps
这样,您可以为正确的任务选择正确的模型,当您遇到问题时,您知道如何修复它们。
事实是,如果你在人工智能领域工作,你不会每次创建一个神经网络时都用手工编码。如果你研究一下人工智能在现实世界中的应用——比如YouTube的推荐系统或SnapChat的换脸过滤器——像TensorFlow和Pytorch这样的库是很常见的。
这是因为这些库是复杂的、易于使用的和高效的。
 但是即使这样,如果您不了解它们是如何工作的,您也不会了解太多。你将无法开发自己的深度学习算法或模型,你也不知道如何调整或改进现有的算法或模型。
但是即使这样,如果您不了解它们是如何工作的,您也不会了解太多。你将无法开发自己的深度学习算法或模型,你也不知道如何调整或改进现有的算法或模型。那么深度学习是如何起作用的呢?
不是作为一种灵活的方式来导入库,而是作为一个数学概念?
好了,系好安全带,兄弟,我们要潜下去了。
深度学习是如何形成的?
虽然人工智能在20世纪50年代到80年代一直是科学家们的热门话题,但这个行业直到最近20年才开始席卷全球。
它最近的普及可以归功于多伦多大学(University of Toronto)教授杰弗里•辛顿(Geoffrey Hinton)在深度学习方面取得的突破,以及世界上计算能力和可用数据量的指数级增长。
[caption id="attachment_47139" align="aligncenter" width="1200"]
 杰弗里·辛顿,被誉为“深度学习的教父”。图片来源于多伦多生活。[/caption]
杰弗里·辛顿,被誉为“深度学习的教父”。图片来源于多伦多生活。[/caption]深度学习是人工智能的一个子集,它使用的算法模仿人类大脑,称为神经网络。
深度学习、更好的硬件和更多的数据的出现,使得以前不可想象的技术得以发展。其中包括实时目标检测和分类算法、自动驾驶汽车、股市预测模型、生成设计软件等等。
神经网络的基本结构
本质上,神经网络学习输入变量和输出变量之间的关系。给定一组x和y的足够数据,神经网络学习准确地从x映射到y。
神经网络由相互连接的处理单元层组成。这些元素被称为“节点”或“神经元”,它们一起工作来解决复杂的问题。节点被组织成层,层又分为三种主要类型:输入层、隐藏层和输出层。

输入层的节点接收输入值,隐藏层的节点执行隐藏计算,输出层的节点返回网络的预测。
假设我们正在训练我们的网络来识别16x16像素网格中的手写数字。为了接收来自该图像的输入,我们将为输入层分配16x16或256个节点。从图像的左上角开始,每个像素由一个节点表示。
[caption id="attachment_47141" align="aligncenter" width="1439"]
 每个像素对应一个输入节点。[/caption]
每个像素对应一个输入节点。[/caption]输入节点将包含-1和1之间的某个数值,以表示其对应像素的亮度,其中-1是深色,1是白的。
当这些值被输入到网络中时,它们就从一个神经元层向前传播到下一个神经元层。
[caption id="attachment_47142" align="aligncenter" width="998"]
 可视化向前传播[/caption]
可视化向前传播[/caption]在它们通过隐藏层中的一系列计算之后,我们期望接收10个输出,其中每个输出节点表示0到9之间的一位数字。
假设,如果我们向网络显示一个手写的“4”,那么网络应该将我们的图像分类为“4”。在数学上,与数字“4”对应的节点将返回输出层中的最高值。
总之,输入层的节点接收输入值,隐藏层的节点执行计算,输出层的节点返回预测。
理解单个节点!⚪
最大的问题是,我们的神经网络如何建立关系模型?为了理解神经网络的工作原理,我们必须首先理解隐藏层中单个节点的功能。我们可以将单个节点的功能与统计学中的一个标志性模型——线性回归的功能进行比较。
线性回归可以定义为对线性关系进行建模的一种尝试。
假设你有一组包含两个定量变量的数据:

如果你将学生的分数与他们在散点图中学习的小时数进行比较,你会发现一个正的线性关系。

一般来说,学生花在学习上的时间越长,他们在考试中取得高分的可能性就越大。线性回归试图做的是通过在散点图上画一条最合适的直线来模拟这种线性关系,我们称之为线性模型。
线性模型基本上是一条直线,y = mx + b,它通过尽可能多的数据。

理想的线性模型应该是最小化学生实际分数与模型预测分数之间的误差,或者最小化模型实际y值与预测y值之间的误差。
让我们仔细看看数学。
在线性模型中,输入x乘以常数m,然后加上输入b,称为“截距”。这些输入相加得到输出y。

得到的直线y = mx + b模拟了x和y之间的关系。
如果我们要修改输入的值,我们需要一条不同的线。例如,将常数b从2变为3意味着将直线向上平移,使其与y轴相交的位置是y = 3而不是y = 2。

我花这么长时间和你一起复习九年级的数学,原因很简单。单个神经元的工作方式完全相同!
在神经元中,输入x₁乘以一个重量,w₁。在我们输入x₁乘以w₁,我们称之为“加权输入”。
然后添加一个常数b₁-它的行为类似于线性模型中的y截距,称为“偏差”。然后将加权输入和偏差相加得到我们的输出,v₀。
[caption id="attachment_47148" align="aligncenter" width="1334"]
 看起来很眼熟,不是吗?[/caption]
看起来很眼熟,不是吗?[/caption]好了!一个基本的神经元。
再次,我们可以通过调整权重w₁或偏差b₁来调整v₀的值。如果我们修改这两个参数中的任何一个,我们将再次期望看到一个不同的线性模型。
原文链接:https://medium.com/datadriveninvestor/deep-learning-is-not-just-import-tensorflow-c27136aaa65e

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























