机器学习模型的特征选择第一部分:启发式搜索
2017年11月26日 由 yuxiangyu 发表
391179
0
特征选择的基础
特征选择能够改善你的机器学习模型。在这个系列中,我简单介绍你需要了解的特征选择的全部内容。本文为第一部分,我将讨论为什么特征选择很重要,以及为什么它实际上是一个非常难以解决的问题。我将详细介绍一些用于解决当前特征选择的不同方法。
我们为什么要关心特征选择?
特征工程对模型质量的影响通常比模型类型或其参数对模型质量的影响更大。而特征选择对于特征工程来说是关键部分,更不用说正在执行隐式特征空间转换的核函数和隐藏层了。在支持向量机(SVM)和深度学习的时代,特征选择仍然具有相关性。
首先,我们可以愚弄最复杂的模型类型。如果我们提供足够的噪音就可以掩盖真实的pattern。在这种情况下,模型开始使用不必要特征的噪音pattern。这意味着它表现不佳。如果过拟合这些pattern,并且在新的数据点上失败,它甚至会变得更糟糕。它让具有多个数据维度的模型来说更加简单。在这方面没有模型类型要比其他更好。决策树可以陷入多层神经网络甚至陷阱。删除噪声特征可以帮助模型聚焦于相关的pattern。
并且特征选择还有其他的好处。如果我们减少特征的数量,模型通常能训练得更快。而所得到的模型更简单,更容易理解。我们应该总是努力使我们的模型更容易工作。聚焦于那些噪声信号的特征,我们将有一个更具鲁棒性的模型。
为什么这是一个难题?
我们从一个例子开始。假设我们有一个包含10个属性(特征,变量,列)和一个标签(目标,类)的数据集。标签栏是我们想要预测的。我们已经对这些数据进行了训练,并确定了模型的精度为62%。我们能否在一个训练好的模型上准确的确定10个属性的子集呢?
我们可以将10个属性的子集描述为位向量,即10个二进制数字的向量。其中0表示不使用特定属性,1表示用于该子集的属性。如果我们要表示使用所有的10个属性,就使用向量(1 1 1 1 1 1 1 1 1 1)。特征选择是产生最优的精度一个位向量的搜索。尝试所有可能的组合是可用的方法之一。我们现在只使用一个属性。第一个位向量看起来像这样:

正如我们所看到的,当我们使用第一个属性时,我们提出了68%的精度。这比我们使用所有属性的精度62%要高得多。现在我们试着只使用第二个属性:

比使用全部10个属性要好,但不如仅使用第一个属性。

我们现在也可以尝试2个属性的子集:
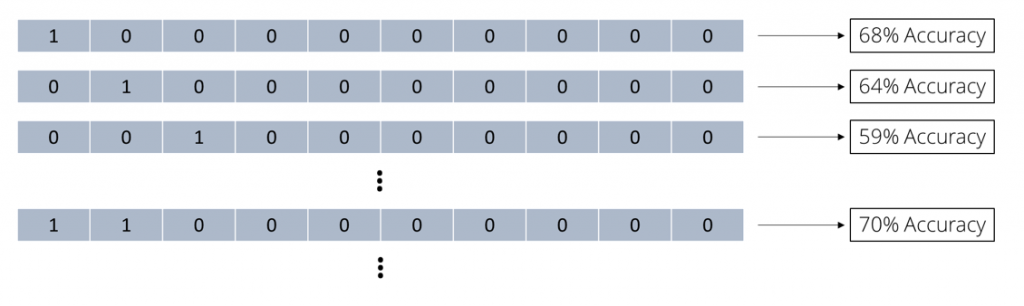
使用前两个属性效果很好,精度达到70%。我们尝试了所有可能的组合,汇总这些子集的所有精度:
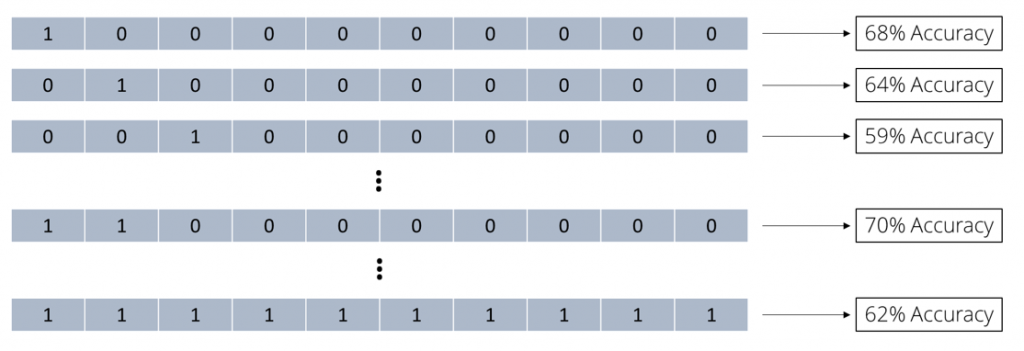
我们称之为穷举搜索法。
那么我们尝试了多少个组合?每个属性有两个选项:我们可以决定是否使用它。我们对所有10个属性做出这个决定,即2 x 2 x 2 x ... = 210或1024个不同的结果。其中的一种组合没有任何意义,也就是说根本不使用任何子集的组合。所以这意味着我们只需要尝试210 - 1 = 1023次子集组合。即使一个小的数据集,我们也可以看到也有有很多属性子集。我们需要为每一个组合进行模型验证。如果我们使用10折交叉验证,我们需要训练10,230个模型。对好的计算机来说这仍然是可行的。
但是更接近实际的数据集呢,例如我们的数据集中有100个属性而不是10个属性,那么我们已经有了2100 -1个组合,约为1.27x 1030。再好的计算机也无法处理这么多组合。
启发式搜索
虽然检查所有可能的属性子集是不可行的。但是,我们可以只关注那些更可能导致更准确模型的组合。我们可以尝试缩减搜索空间,忽略不可能产生好模型的特征集。不过,我们当然不能保证我们会找到最优解。如果我们没有使用完整的搜索空间,也许会跳过最优解,但是这种方法比穷举的方法要快得多。而且,我们通常会以更快的速度获得很好解决方案,有时甚至会获得最优解。在机器学习中有两种广泛使用的特征选择启发式搜索方法。我们称之为前向选择和后向消除。
前向选择
前向选择背后的启发非常简单。我们首先尝试所有只使用一个属性的子集,并保留最优解。但是,接下来不是尝试所有可能的具有两个特征的子集,而只是尝试特定的2个子集组合。我们尝试包含上一轮最佳属性的2个子集。如果没有改进,就停止操作并提供最好的结果,即单一的属性。但是,如果我们提高了精度,就保留最好的属性,并尝试添加一个。重复此过程,直到我们不再需要改进。
对于我们以上述10个属性为例?我们从10个模型评估中只有一个属性的10个子集开始。然后,我们保留最佳性能属性,并尝试它与其他属性的9个可能组合。如果我们没有得到更好的精度那就停止。否则,我们继续尝试8个可能的3个子集。于是,我们最多通过10 + 9 + ... + 1 = 55个子集。并且没有进一步的改善,我们往往会提早停止。这样,运行时间的会显著减少。具有100个属性的情况,差异变得更加明显。
后向消除
操作与前向选择类似,但方向相反。我们首先从所有属性组成的子集开始。然后,我们尝试每次删除一个单一属性。如果有所改善,我们就继续操作。并且我们仍然把这个导致精度最大提高的属性(即去掉它精度最高的属性)忽略掉。然后我们继续消除一个属性来完成所有可能的组合,直到精度不再改善。同样地,对于10个属性我们我们需要评估至多1 + 10 + 9 + 8 + ... + 2 = 55的组合。
现在我们找到了比穷举搜索更快的启发式搜索。在某些情况下,这些方法将提供一个非常好的属性子集。但大多数情况下,他们不幸的是不会。对于大多数数据集,模型精度形成了多模式适应度地形(multi-modal fitness landscape)。也就是说除了一个全局最优值之外,还有几个局部最优值。这两种方法将开始在这个适应度的某个地方,并从那里移动。在下面的图片中,我们用红点标出了这样一个起点。从那里,我们继续增加(或删除)属性,如果适应度提高。他们将永远爬上多模式适应度地形中最近的山丘。如果这个山丘是一个局部最优值,他们会被卡在那里,因为没有进一步的攀登可能。因此,这些算法根本不去寻找更高的山丘。他们只拿走他们可以轻易得到的东西。这正是我们称之为“贪心”算法的原因。而当他们停止改进时,他们停留在最高的山顶上只有很小的可能性。他们更有可能错过了我们正在寻找的全局最优解。这意味着他们得出的特征子集通常是次优的结果。
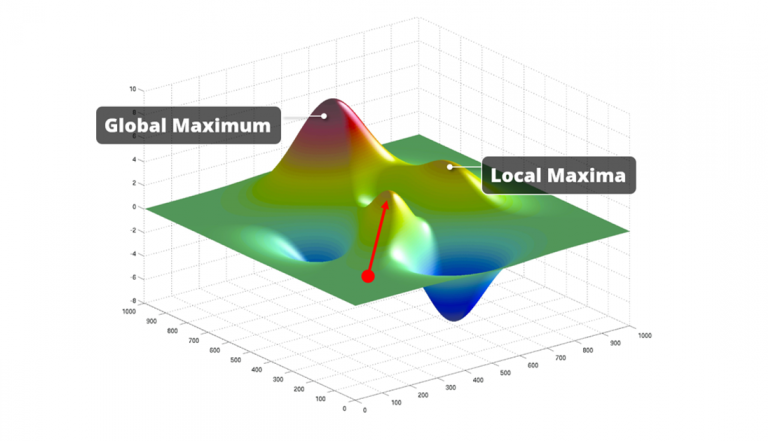
是否还有更好的方法呢
我们有一种技术可以提供最佳结果,但在计算上不可行。正如我们所看到的,我们根本不能在现实的数据集上使用穷举搜索。而我们的两种启发式方法,即前向选择和后向消除方法,可以更快地提供结果。但智能发现的第一个局部最优值。这意味着他们很大可能不会提供最佳结果。
那么,在我们的下一篇文章中,我们将讨论另一种启发式搜索,既可以在更大的数据集上使用,也往往比前向选择和后向消除提供更好的结果。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























