机器学习入门教程：Python测试线性可分性的方法

2018年01月08日由 yining 发表 919327 0

线性和非线性分类
两个子集是线性可分的,如果存在一个超平面将每组的元素的所有元素的一组驻留在另一侧的超平面其他设置。我们可以描述它在2D绘图中通过分离线,并且在3D绘图通过一个超平面。

根据定义，线性可分性定义为:如果存在 $机器学习入门教程：Python测试线性可分性的方法$ , $机器学习入门教程：Python测试线性可分性的方法$ 和 $机器学习入门教程：Python测试线性可分性的方法$ ，那么两组集合 $机器学习入门教程：Python测试线性可分性的方法$ 和 $机器学习入门教程：Python测试线性可分性的方法$ 是线性可分的。

简而言之，如果存在一个超平面完全分离H元素和M元素，那么上面的表达式表示H和M是线性可分的。

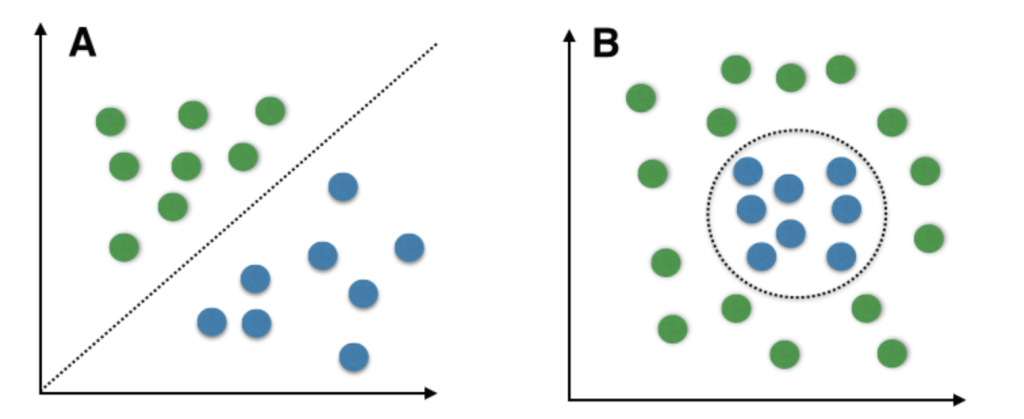
图片来源：Sebastian Raschka 2

在上图中，A显示了一个线性分类问题，B显示了一个非线性的分类问题。在A中，我们的决策边界是一个线性的，它将蓝色的点和绿色的点完全分开。在这个场景中，可以实现几个线性分类器。

在B中，我们的决策边界是非线性的，我们将使用非线性的核函数和其他非线性的分类算法和技术。

一般来说，在机器学习中，在运行任何类型的分类器之前，理解我们要处理的数据是很重要的，以确定应该从哪一种算法开始，以及我们需要调整哪些参数来适应任务。如果我们的问题是线性的或者非线性的，这就会给我们带来线性可分性和理解的问题。

如上所述，有几种分类算法是通过构造一个线性决策边界(超平面)分类来分离这些数据的，而这样做的假设是:数据是线性可分的。然而，在实际操作中，事情并非那么简单，许多情况下的数据可能不是线性可分的，因此应用了非线性技术。线性和非线性技术的决策是基于数据科学家所知道的最终目标,他们愿意接受的错误,平衡模型复杂性和泛化,偏见方差权衡等等。

这篇文章的灵感来自于线性可分性问题的研究论文，论文地址如下：

1.《线性可分性问题:一些测试方法》: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.121.6481&rep=rep1&type=pdf

2.《线性可分性测试的一个简单算法》:http://mllab.csa.iisc.ernet.in/downloads/Labtalk/talk30_01_08/lin_sep_test.pdf

本文的目标是在Python中应用和测试少数技术，并演示如何实现它们。测试线性可分性的一些技术是:

领域和专业知识

数据可视化

计算几何学(凸包)

机器学习:
- 感知器
- 支持向量机

领域和专业知识

这应该是显而易见的，第一步应该是寻求分析师和其他已经熟悉数据的数据科学家的见解。在开始任何数据发现之旅前学会先问问题,以便更好地理解任务的目的(你的目标),并在早期获得来自领域专家的见解。

获得数据
对于上面列出的其他三种方法，我们将使用传统的Iris数据集（鸢尾花数据集）来探索这些概念，并使用Python实现线性可分测试的一些理论。

Iris数据集：https://archive.ics.uci.edu/ml/datasets/iris

因为这是一个众所周知的数据集，我们预先知道哪些类是线性可分的。对于我们的分析，我们将使用这些已知的知识来证实我们的发现。

Iris以鸢尾花的特征作为数据来源，数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性，是在数据挖掘、数据分类中非常常用的测试集、训练集。

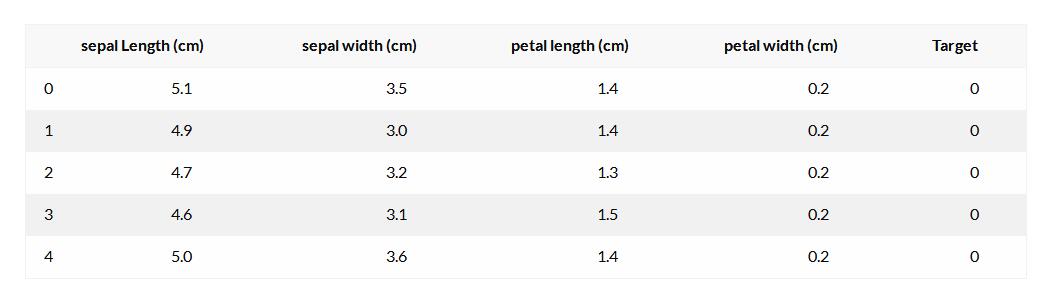
首先，导入必要的库并加载数据。

import numpy as np 

import pandas as pd 

import matplotlib.pyplot as plt 



from sklearn import datasets 

data = datasets.load_iris() 



#create a DataFrame 

df = pd.DataFrame(data.data, columns=data.feature_names) 

df['Target'] = pd.DataFrame(data.target) 

df.head()

数据可视化

最简单和最快速的方法是可视化数据。如果特性（feature）的数量很大，那么这种方法可能是不可行的，或者说太过直接了，因此很难在2D中绘图。在这种情况下，我们可以使用Pair Plot方法，并且Pandas库为我们使用scatter_matrix提供了一个很好的选项:

from pandas.tools.plotting import scatter_matrix

scatter_matrix(df.iloc[:,0:4], figsize=(15,11))

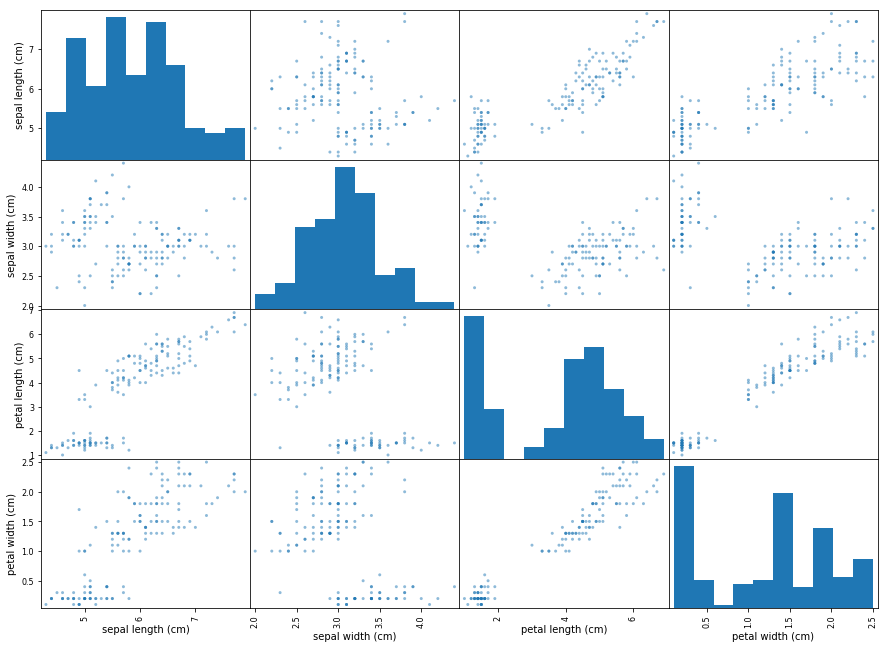机器学习入门教程：Python测试线性可分性的方法上面的散布矩阵是数据集中所有特性的一个成对的散点图(我们有4个特征，所以我们得到一个4×4矩阵)。散布矩阵提供了关于这些变量是如何相互关联的见解。让我们通过创建一个散布矩阵中花瓣的长度（Petal Length）和花瓣宽度（Petal Width）的散点图来展开这一扩展。

plt.clf()

plt.figure(figsize=(10,6))

plt.scatter(df.iloc[:,2], df.iloc[:,3])

plt.title('Petal Width vs Petal Length')

plt.xlabel(data.feature_names[2])

plt.ylabel(data.feature_names[3])

plt.show()

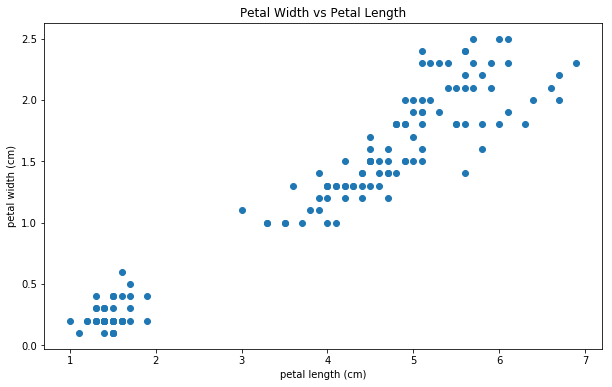它仍然没有那么有用。让我们给每个类着色，并添加一个图例，这样我们就能理解图中每个类的数据分布，并确定这些类是否可以被线性分离。

让我们更新我们的代码:

plt.clf()

plt.figure(figsize = (10, 6))

names = data.target_names

colors = ['b','r','g']

label = (data.target).astype(np.int)

plt.title('Petal Width vs Petal Length')

plt.xlabel(data.feature_names[2])

plt.ylabel(data.feature_names[3])

for i in range(len(names)):

 bucket = df[df['Target'] == i]

 bucket = bucket.iloc[:,[2,3]].values

 plt.scatter(bucket[:, 0], bucket[:, 1], label=names[i]) 

plt.legend()

plt.show()

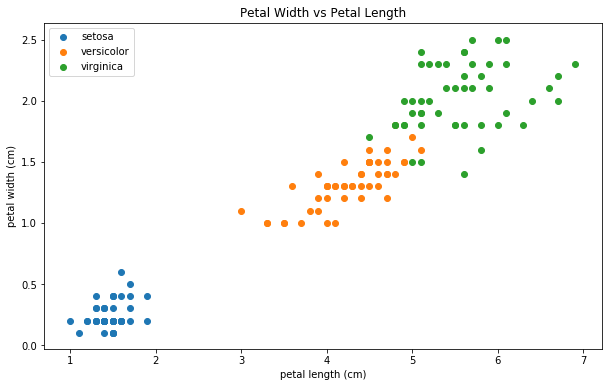
看上去好多了。我们只是绘制了整个数据集，所有150个点。每个类有50个数据点。是的，乍一看，我们可以看到蓝色的点(Setosa类)可以很容易地通过画一条线来分隔，并将其与其他类隔离开来。但是其他两个类呢?

让我们检查另一种更确定的方法。

计算几何学

在这种方法中，我们将使用凸包（Convex Hull）来检查一个特定的类是否是线性可分的。简而言之，凸包代表了一组数据点(类)的外边界，这就是为什么有时它被称为凸包。

当测试线性可分性时使用凸包的逻辑是相当直接的，可以这样说:

如果X和Y的凸包的交点是空的，那么两个类X和Y是线性可分的。

一种快速的方法来查看它是如何工作的，就是将每个类的凸包的数据点可视化。我们将绘制凸包边界，以直观地检查交点。我们将使用Scipy库来帮助我们计算凸包。更多信息请参阅下方Scipy文档地址。

地址：https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.ConvexHull.html

让我们更新前面的代码，以包含凸包。

from scipy.spatial import ConvexHull

 

plt.clf()

plt.figure(figsize = (10, 6))

names = data.target_names

label = (data.target).astype(np.int)

colors = ['b','r','g']

plt.title('Petal Width vs Petal Length')

plt.xlabel(data.feature_names[2])

plt.ylabel(data.feature_names[3])

for i in range(len(names)):

 bucket = df[df['Target'] == i]

 bucket = bucket.iloc[:,[2,3]].values

 hull = ConvexHull(bucket)

 plt.scatter(bucket[:, 0], bucket[:, 1], label=names[i]) 

 for j in hull.simplices:

 plt.plot(bucket[j,0], bucket[j,1], colors[i])

plt.legend()

plt.show()

我们的输出看起来像这样：

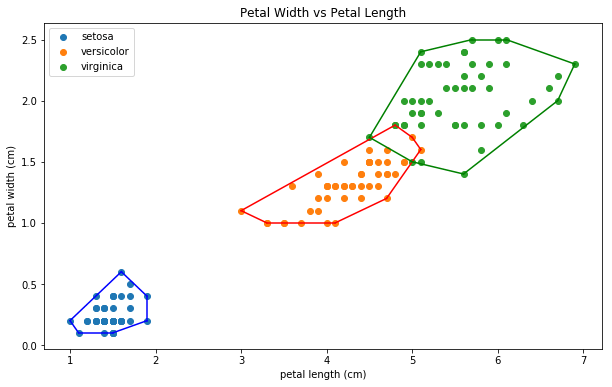机器学习入门教程：Python测试线性可分性的方法

至少从直观上看，Setosa是一个线性可分的类。换句话说，我们可以很容易地画出一条直线，将Setosa类与非Setosa类分开。Versicolor类和Versicolor类都不是线性可分的，因为我们可以看到它们两个之间确实有一个交集。

机器学习

在本节中，我们将研究两个分类器，用于测试线性可分性:感知器(最简单的神经网络)和支持向量机(称为核方法的一部分)

单层感知器
感知器（perceptron）是一种用于二进制分类的算法，属于一类线性分类器。在二进制分类中，我们尝试将数据分成两个Bucket:要么是在Buket A或 Bucket B中，或是更简单的:要么是在Bucket A中，要么不在Bucket A中(假设我们只有两个类)，因此命名为二进制分类。

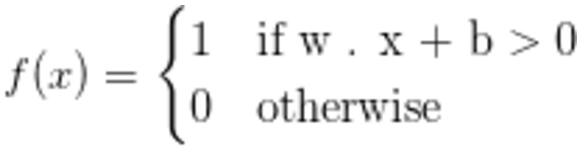
机器学习入门教程：Python测试线性可分性的方法

只有当输入向量是线性可分的时，一个单层感知器才会收敛。在这个状态下，所有输入向量都将被正确地分类，表示线性可分性。如果它们不是线性可分的，它就不会收敛。换句话说，如果数据集不是线性可分的，它就不能正确地分类。对于我们的测试目的，这正是我们所需要的。

我们将把它应用在整个数据上，而不是将它分割成测试/训练，因为我们的目的是测试类之间的线性可分性，而不是为将来的预测建立模型。

我们将使用Scikit-Learn并选择感知器作为我们的线性模型选择。在此之前，让我们做一些基本的数据预处理任务:

# Data Preprocessing

x = df.iloc[:, [2,3]].values

# we are picking Setosa to be 1 and all other classes will be 0

y = (data.target == 0).astype(np.int) 

 

#Perform feature scaling

from sklearn.preprocessing import StandardScaler

sc= StandardScaler()

x = sc.fit_transform(x)

现在，让我们来构建我们的分类器：

from sklearn.linear_model import Perceptron

perceptron = Perceptron(random_state = 0)

perceptron.fit(x, y)

predicted = perceptron.predict(x)

为了更好地理解结果，我们将绘制混淆矩阵和决策边界。

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y, predicted)

 

plt.clf() 

plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Wistia)

classNames = ['Negative','Positive']

plt.title('Perceptron Confusion Matrix - Entire Data')

plt.ylabel('True label')

plt.xlabel('Predicted label')

tick_marks = np.arange(len(classNames))

plt.xticks(tick_marks, classNames, rotation=45)

plt.yticks(tick_marks, classNames)

s = [['TN','FP'], ['FN', 'TP']]

 

for i in range(2):

 for j in range(2):

 plt.text(j,i, str(s[i][j])+" = "+str(cm[i][j]))

plt.show()

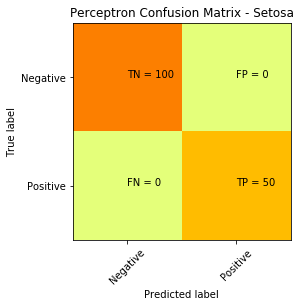
现在，让我们绘制出决策边界：

from matplotlib.colors import ListedColormap

plt.clf()

X_set, y_set = x, y

X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),

 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))

plt.contourf(X1, X2, perceptron.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),

 alpha = 0.75, cmap = ListedColormap(('navajowhite', 'darkkhaki')))

plt.xlim(X1.min(), X1.max())

plt.ylim(X2.min(), X2.max())

for i, j in enumerate(np.unique(y_set)):

 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],

 c = ListedColormap(('red', 'green'))(i), label = j)

plt.title('Perceptron Classifier (Decision boundary for Setosa vs the rest)')

plt.xlabel('Petal Length')

plt.ylabel('Petal Width')

plt.legend()

plt.show()

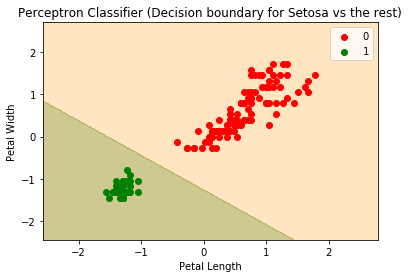
我们可以看到，我们的感知器确实收敛了，并能够将Setosa从非Setosa中区分出来，因为数据是线性可分的。如果数据不是线性可分的，情况就不一样了。让我们在另一个类上试一下。

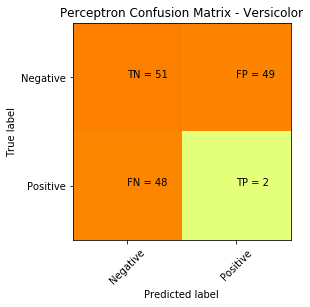
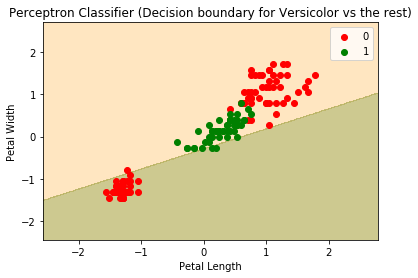
以下是Versicolor类(试图将Versicolor与剩下的类分开）: 机器学习入门教程：Python测试线性可分性的方法

支持向量机
现在，让我们用一个核函数的支持向量机来检查另一种方法。为了测试线性可分性，我们将选择一个核函数的硬间隔（hard-margin）(最大距离，反义词为soft-margin)支持向量机。现在，如果我们的目的是训练一个模型，我们的选择将会完全不同。但是，由于我们正在测试线性可分性，所以我们想要一个能够失败的严格的测试(或者如果不收敛的话就会产生错误的结果)来帮助我们更好地评估手头的数据。

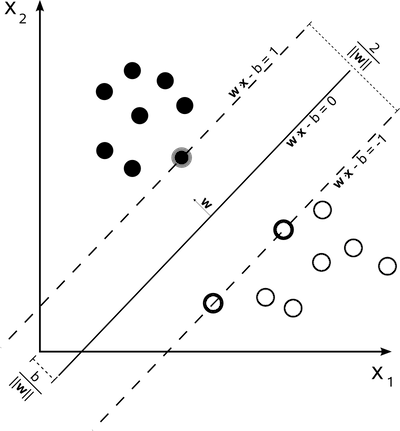
机器学习入门教程：Python测试线性可分性的方法

图片来源：维基百科

现在，让我们编码：

from sklearn.svm import SVC

svm = SVC(C=1.0, kernel='linear', random_state=0)

svm.fit(x, y)

 

predicted = svm.predict(x)

 

cm = confusion_matrix(y, predicted)

 

plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Wistia)

classNames = ['Negative','Positive']

plt.title('SVM Linear Kernel Confusion Matrix - Setosa')

plt.ylabel('True label')

plt.xlabel('Predicted label')

tick_marks = np.arange(len(classNames))

plt.xticks(tick_marks, classNames, rotation=45)

plt.yticks(tick_marks, classNames)

s = [['TN','FP'], ['FN', 'TP']]

 

for i in range(2):

 for j in range(2):

 plt.text(j,i, str(s[i][j])+" = "+str(cm[i][j]))

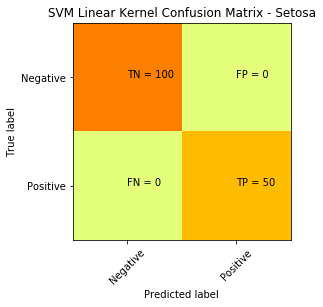
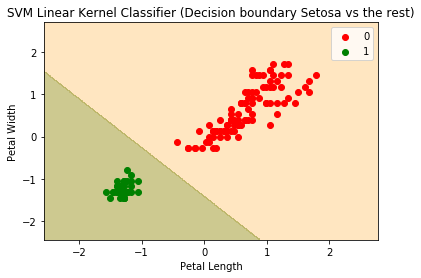
下面是混淆矩阵和决策边界的图: 机器学习入门教程：Python测试线性可分性的方法

完美的分离/分类指示一个线性可分性。

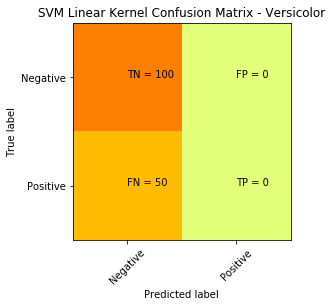
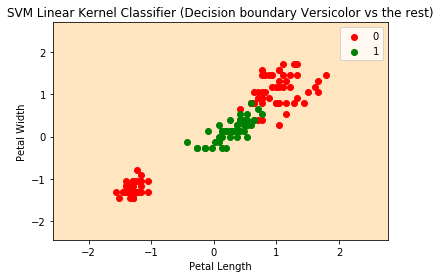
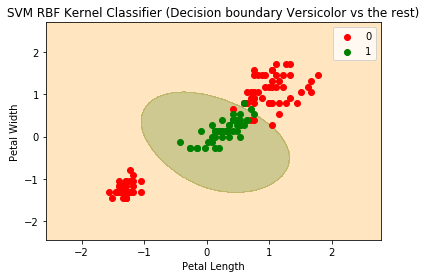
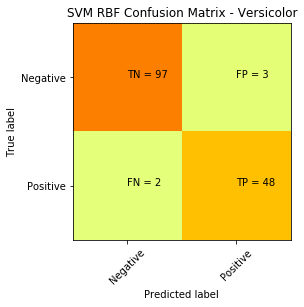
现在，让我们来测试一下，对Versicolor类进行测试，我们得到了下面的绘图。有趣的是，我们没有看到一个决策边界，而混淆矩阵表示分类器的工作完成得并不好。机器学习入门教程：Python测试线性可分性的方法

现在，为了好玩，并且可以演示出支持向量机的强大功能，让我们应用一个非线性的内核。在这种情况下，我们将应用一个径向基函数（RBF Kernel）对上面的代码稍微改动一下，得到了完全不同的结果:

x = df.iloc[:, [2,3]].values

y = (data.target == 1).astype(np.int) # we are picking Versicolor to be 1 and all other classes will be 0

 

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()

x = sc.fit_transform(x)

 

from sklearn.svm import SVC

svm = SVC(kernel='rbf', random_state=0)

svm.fit(x, y)

 

predicted = svm.predict(x)

 

cm = confusion_matrix(y, predicted)

 

plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Wistia)

classNames = ['Negative','Positive']

plt.title('SVM RBF Confusion Matrix - Versicolor')

plt.ylabel('True label')

plt.xlabel('Predicted label')

tick_marks = np.arange(len(classNames))

plt.xticks(tick_marks, classNames, rotation=45)

plt.yticks(tick_marks, classNames)

s = [['TN','FP'], ['FN', 'TP']]

 

for i in range(2):

 for j in range(2):

 plt.text(j,i, str(s[i][j])+" = "+str(cm[i][j]))

Python源代码：https://github.com/tatwan/Linear-Separability/blob/master/linear_separability.py

标签：

Python 学习人工智能教程

0 评论

欢迎关注ATYUN官方公众号

商务合作及内容投稿请联系邮箱:bd@atyun.com

上一篇在C ++中使用TensorFlow训练深度神经网络

下一篇想知道比特币价格趋势？本文带你一探究竟

评论登录

要发表评论，您必须先登录。

jonatasgrosman/wav2vec2-large-xlsr-53-english facebook/dino-vitb16 bert-base-uncased xlm-roberta-large xlm-roberta-base gpt2 microsoft/resnet-50 facebook/dino-vits8

Sam Altman离职事件时间线