Ferenc Huszár:剪枝神经网络两篇最新论文的解读
2018年02月22日 由 yuxiangyu 发表
435939
0
我想简要地介绍两篇关于修剪神经网络的论文:
Learning Sparse Neural Networks through L0 Regularization - Christos Louizos, Max Welling, Diederik P. Kingma (2018)
链接:https://arxiv.org/abs/1712.01312
Faster gaze prediction with dense networks and Fisher pruning - Lucas Theis, Iryna Korshunova, Alykhan Tejani, Ferenc Huszár (2018)
链接:https://arxiv.org/abs/1801.05787
我在本文中提到的剪枝(pruning),是指减少或控制非零参数的数量,或者在神经网络中使用很多特征映射。在高维中,至少有三种方法可以做到这一点,而剪枝就是其中之一:
你可能会出于很多目的修建自己的网络。最可能的原因是在保持相同的性能的同时降低计算成本。删除那些深度网络架构中没有真正使用的特征可以加速推理和训练。你也可以把剪枝看作是一种架构搜索的形式:搞清每层中需要多少特征才能获得最佳性能。
其次你可能因为需要通过减少参数数量来增强泛化,减少参数空间的冗余。正如我们在近期关于深度网络中泛化的研究中所看到的那样,参数的原始数量(L 0 L 0
我发现Louizos等人的L0论文很有意思,它可以被看作是之前我写的机器学习文章中,关于机器学习问题转换的简单应用。这是一个很好的例子,说明如何使用这些想法,为一个棘手的ML优化问题订制实际的你可以运行的随机梯度下降算法。
链接:http://www.inference.vc/design-patterns/
所以我将把论文总结成一系列的步骤,每一步都改变了优化问题:
有趣的是,(3)式和进化策略或变分优化之间的联系没有被提到。取而代之的是,基于spike-and-slab先验的激励。我建议阅读这篇论文,也考虑到这一点。
然后,作者证明这确实是可行的,并且与其他设计用于减少参数数量的方法相比更有优势。根据这些步骤从一个问题转换到另一个问题的思考,可以让你概括或改进这种想法。例如,REBAR或RELAX梯度估计器提供了一个没有偏见的,低方差的替代concrete relaxation,也可以很好地工作。
我想谈的第二篇文章是来自我们自己的实验室。不是纯粹的方法论文,而着重于建立轻便的神经网络来预测图像显著性的具体应用。修剪后的网络现在提供了支持在Twitter上裁剪照片的逻辑。
我们的目标也是降低网络的计算成本,特别是在迁移学习环境中:当在预训练完成的神经网络的基础上构建时,你将继承解决原始源任务所需的大量复杂度,这对于解决你的目标任务是多余的。我们的高级修剪目标不同的地方在于:不像L0范数或组稀疏,我们用一个稍微复杂的公式来直接估计方法的正向通道运行时间。这是每个层的参数个数与相邻层之间的相互作用的二次函数。有趣的是,这会导致架构倾向于交替厚层和薄层,如下所示:
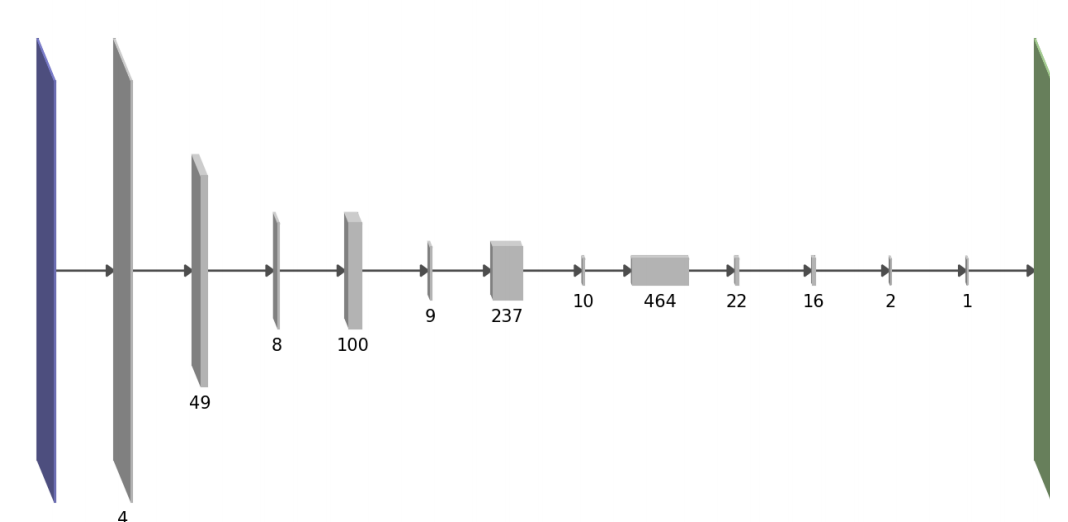
我们“贪婪”地剪掉训练好的网络,每次去掉一个卷积特征映射。选择下一个修剪特征映射去剪枝的一个原则是尽量减少由此造成的训练损失的增加。从这个标准出发,使用损失的二阶泰勒展开,做更多的假设,我们得到下面的剪枝表达式(pruning signal)来保持参数θi。
Δi∝Fiθi2
其中Fi表示费希尔信息矩阵的ith对角项。上面的公式删除的是单个参数,但是我们可以拓展它,删除全部特征映射。通过删除每次迭代具有最小Δ的参数或特征映射进行修剪,并在迭代之间对网络进行再训练网络。
这本文中,我项支出费希尔剪枝与我之前曾发的博客中的观点之间的联系。
博客:http://www.inference.vc/
第一个联系是Fisher-Rao范数(FR-norm)。假设费希尔信息对角 - 理论上是一个不合理的假设,但是实际上的简化在实践中产生了有用的算法。因为这个假设,关于θ的变为:
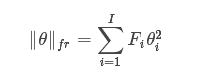
用这种形式写下来,你可以希望看到Fisher-Rao范数和费希尔修剪标准之间的联系。根据所使用的费希尔信息的特定定义,可以近似解释FR-norm:
在现实世界中,Fisher信息矩阵并不对角,这实际上对理解泛化非常重要。举个例子,只考虑对角项使得费希尔剪枝对网络的某些重新参数化(非对角线雅可比行列式)敏感。但是也许在Fisher-Rao范数和参数的冗余之间有更深的联系。
利用对角费希尔信息值,引导剪枝与弹性权重巩固( EWC,elastic weight consolidation) 。在EWC中,费希尔信息值用于确定权重对于解决以前的任务的重要程度。这个算法是从贝叶斯在线学习的角度推导出来的,但你也可以从泰勒展开的角度来激发它,就像费希尔剪枝一样。
为了解释EWC你可以把他看作共享硬盘(只是比喻)。神经网络的参数就像一个硬盘驱动器或某种存储卷。在任务中训练神经网络包括压缩训练数据并保存信息到硬盘。如果你没有防止数据被覆盖的机制,那么它将会被覆盖:在神经网络中,灾难性的遗忘会以同样的方式发生。EWC就像一个在多个用户之间共享硬盘的协议,用户不会覆盖对方的数据。EWC中的费希尔信息值可以被看作软的不覆盖的标志。在对第一个任务进行训练之后,我们计算出费希尔信息值,该值表示哪些参数存储任务的关键信息。较低的费希尔值是冗余的,可以重复使用来存储新的信息。在这个比喻中,我们可以想到费希尔信息值的总和能衡量硬盘驱动器满载的程度,而剪枝就像丢弃了实际上没有存储任何东西的驱动器部分。
我记述了两个通过计算出哪些参数或特征可以扔掉来自动学习神经网络架构的方法。在我看来,这两种方法或者说论文本身都很有趣。L0方法似乎是一种更简单的优化算法,可能比费希尔剪枝的迭代,每次删除一个特征的性质更可取。然而,当你从一个大的预训练模式开始,费希尔修剪更适用于,在迁移学习的环境中,从大的预训练模型开始的这种情况。
Learning Sparse Neural Networks through L0 Regularization - Christos Louizos, Max Welling, Diederik P. Kingma (2018)
链接:https://arxiv.org/abs/1712.01312
Faster gaze prediction with dense networks and Fisher pruning - Lucas Theis, Iryna Korshunova, Alykhan Tejani, Ferenc Huszár (2018)
链接:https://arxiv.org/abs/1801.05787
我在本文中提到的剪枝(pruning),是指减少或控制非零参数的数量,或者在神经网络中使用很多特征映射。在高维中,至少有三种方法可以做到这一点,而剪枝就是其中之一:
- 正则化:修改目标函数或学习问题,所以优化可能会找到一个参数较少的神经网络。第一篇论文选择了这种方法。
- 剪枝:取一个大的网络,删除一些多余的特征或参数。第二篇论文选择了这种方法。
- 成长(growing):第三种方法,从小型网络开始,通过增加标准逐步增加新的单元。比较少见。
为什么需要这样做?
你可能会出于很多目的修建自己的网络。最可能的原因是在保持相同的性能的同时降低计算成本。删除那些深度网络架构中没有真正使用的特征可以加速推理和训练。你也可以把剪枝看作是一种架构搜索的形式:搞清每层中需要多少特征才能获得最佳性能。
其次你可能因为需要通过减少参数数量来增强泛化,减少参数空间的冗余。正如我们在近期关于深度网络中泛化的研究中所看到的那样,参数的原始数量(
L0正则化
我发现Louizos等人的L0论文很有意思,它可以被看作是之前我写的机器学习文章中,关于机器学习问题转换的简单应用。这是一个很好的例子,说明如何使用这些想法,为一个棘手的ML优化问题订制实际的你可以运行的随机梯度下降算法。
链接:http://www.inference.vc/design-patterns/
所以我将把论文总结成一系列的步骤,每一步都改变了优化问题:
- 从理想的损失函数开始,虽然它可能很难优化:通常的训练损失加参数的L0范数线性结合。在L0范数计算向量中非零项,这是一个不可微分的分段常值函数。这是一个困难的组合优化问题。
- 应用变分优化将不可微函数转化为可微函数。通常通过在参数θ中引入概率分布pψ(θ)来进行。即使目标相对于任何
θ ">θ都不可微分,pψ(θ)以下平均损失可能是可微的,与θ有关。为了找到最佳的ψ,通常可以使用增强(REINFORCE)梯度估计器,从而形成进化策略。但是一般都有很高的方差。 - 所以,我们将再参量化(reparametrization)技巧应用于pψ
p ψ - 为了处理离散变量,我将它转换成concrete relaxation,它通过一个连续的近似来逼近离散的随机变量。现在我们有一个较低的方差(与REINFORCE相比)梯度估计器,可以通过反向传播和蒙特卡罗采样来计算。你可以在随即梯度下降((Adam))中使用这些梯度,这也正是论文中的做法。
有趣的是,(3)式和进化策略或变分优化之间的联系没有被提到。取而代之的是,基于spike-and-slab先验的激励。我建议阅读这篇论文,也考虑到这一点。
然后,作者证明这确实是可行的,并且与其他设计用于减少参数数量的方法相比更有优势。根据这些步骤从一个问题转换到另一个问题的思考,可以让你概括或改进这种想法。例如,REBAR或RELAX梯度估计器提供了一个没有偏见的,低方差的替代concrete relaxation,也可以很好地工作。
费希尔剪枝
我想谈的第二篇文章是来自我们自己的实验室。不是纯粹的方法论文,而着重于建立轻便的神经网络来预测图像显著性的具体应用。修剪后的网络现在提供了支持在Twitter上裁剪照片的逻辑。
我们的目标也是降低网络的计算成本,特别是在迁移学习环境中:当在预训练完成的神经网络的基础上构建时,你将继承解决原始源任务所需的大量复杂度,这对于解决你的目标任务是多余的。我们的高级修剪目标不同的地方在于:不像L0范数或组稀疏,我们用一个稍微复杂的公式来直接估计方法的正向通道运行时间。这是每个层的参数个数与相邻层之间的相互作用的二次函数。有趣的是,这会导致架构倾向于交替厚层和薄层,如下所示:

我们“贪婪”地剪掉训练好的网络,每次去掉一个卷积特征映射。选择下一个修剪特征映射去剪枝的一个原则是尽量减少由此造成的训练损失的增加。从这个标准出发,使用损失的二阶泰勒展开,做更多的假设,我们得到下面的剪枝表达式(pruning signal)来保持参数θi。
Δi∝Fiθi2
其中Fi表示费希尔信息矩阵的ith对角项。上面的公式删除的是单个参数,但是我们可以拓展它,删除全部特征映射。通过删除每次迭代具有最小Δ的参数或特征映射进行修剪,并在迭代之间对网络进行再训练网络。
这本文中,我项支出费希尔剪枝与我之前曾发的博客中的观点之间的联系。
博客:http://www.inference.vc/
Fisher-Rao范数
第一个联系是Fisher-Rao范数(FR-norm)。假设费希尔信息对角 - 理论上是一个不合理的假设,但是实际上的简化在实践中产生了有用的算法。因为这个假设,关于θ的变为:
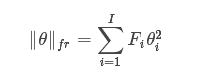
用这种形式写下来,你可以希望看到Fisher-Rao范数和费希尔修剪标准之间的联系。根据所使用的费希尔信息的特定定义,可以近似解释FR-norm:
- 当你删除一个随机参数时,训练日子的可能性(费希尔经验信息)下降。
- 或者当移除一个参数时,模型(费希尔信息模型)定义的条件分布近似变化。
在现实世界中,Fisher信息矩阵并不对角,这实际上对理解泛化非常重要。举个例子,只考虑对角项使得费希尔剪枝对网络的某些重新参数化(非对角线雅可比行列式)敏感。但是也许在Fisher-Rao范数和参数的冗余之间有更深的联系。
弹性权重巩固
利用对角费希尔信息值,引导剪枝与弹性权重巩固( EWC,elastic weight consolidation) 。在EWC中,费希尔信息值用于确定权重对于解决以前的任务的重要程度。这个算法是从贝叶斯在线学习的角度推导出来的,但你也可以从泰勒展开的角度来激发它,就像费希尔剪枝一样。
为了解释EWC你可以把他看作共享硬盘(只是比喻)。神经网络的参数就像一个硬盘驱动器或某种存储卷。在任务中训练神经网络包括压缩训练数据并保存信息到硬盘。如果你没有防止数据被覆盖的机制,那么它将会被覆盖:在神经网络中,灾难性的遗忘会以同样的方式发生。EWC就像一个在多个用户之间共享硬盘的协议,用户不会覆盖对方的数据。EWC中的费希尔信息值可以被看作软的不覆盖的标志。在对第一个任务进行训练之后,我们计算出费希尔信息值,该值表示哪些参数存储任务的关键信息。较低的费希尔值是冗余的,可以重复使用来存储新的信息。在这个比喻中,我们可以想到费希尔信息值的总和能衡量硬盘驱动器满载的程度,而剪枝就像丢弃了实际上没有存储任何东西的驱动器部分。
总结
我记述了两个通过计算出哪些参数或特征可以扔掉来自动学习神经网络架构的方法。在我看来,这两种方法或者说论文本身都很有趣。L0方法似乎是一种更简单的优化算法,可能比费希尔剪枝的迭代,每次删除一个特征的性质更可取。然而,当你从一个大的预训练模式开始,费希尔修剪更适用于,在迁移学习的环境中,从大的预训练模型开始的这种情况。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























