本文讨论一种称为正则化贪心森林（Regularized Greedy Forests，RGF）的算法。它的性能与执行在较大数据集的梯度下降算法类似。它们产生较少的相关性预测，并且能很好地与其他梯度下降决策树模型集成。

为了充分理解本文，应该了解梯度下降和决策树的基础知识。

RGF与梯度下降

在梯度下降算法中，每个分类器/回归器都接受了数据的训练，继承了以前的分类器/回归器的成果。在每次训练后，重新分配权重。为错误分类的数据增加权重，以强调最困难的情况。这样，后续的学习器（learner）会在他们的训练中关注他们。



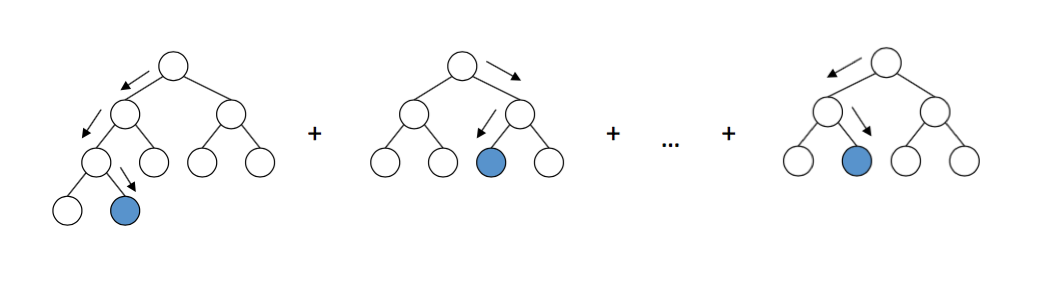
但是，这种方法把基于学习器的决策树视为一个黑盒子，没有利用树结构本身。从某种意义上说，梯度下降对模型执行部分校正步骤。

而RGF执行两个步骤：

1. 找到当前森林某一步的结构变化，以获得最小化损失函数的新森林（例如最小二乘法或logloss）


2. 调整整个森林的“叶子”的权重，使损失函数最小化

寻找最佳的结构变化：

1. 为了计算效率，在搜索策略中仅执行两种类型的操作：
   ·分割现有的叶节点
   ·启动一个新的树（即向森林添加新的树根）。


2. 通过反复评估所有可能的结构变化的最大损失率，对所有现有叶节点的权重进行搜索。


3. 想要搜索整个森林非常困难（实际应用时通常如此）。因此，搜索仅限于最近创建的“t”树，默认选项为t = 1。

在这里，我来举个例子来说明一下。

图型3显示了在与图型2相同的阶段，我们可以考虑拆分标记为X的一个叶节点或者生成一个新的树T4。

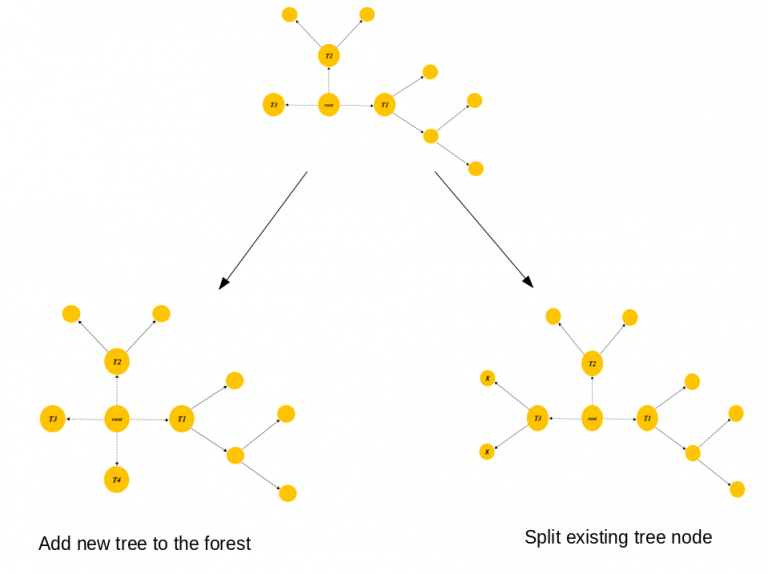
权重优化

每个节点的权重也被优化，以进一步最小化损失函数：

1. 损失函数和权重优化的区间可以由参数指定。每次增加100（k = 100）个新的叶节点，校正权重就能很好地工作，所以当RGF模型被训练时，这被作为默认参数。


2. 如果“k”非常大，那么类似于在重点做单一权重的更新; 如果“k”’非常小（例如k = 1），那么它会大大减慢训练速度。

正则化

在这里为损失函数正则化对于这个算法来说是非常重要的，因为它会很快过拟合。森林生长过程和权重校正过程可能有不同的L2正则化参数。

有三种正则化的方法：

1.一个是单叶（leaf-only）模型的L2正则化，其中正则化惩罚项G(F)为:：



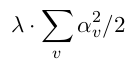
2.另外两个被称为最小惩罚正则化（min-penalty regularizers）。他们对每棵树的正则化惩罚项的定义是：

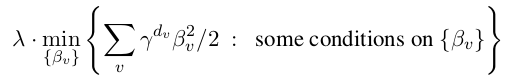
更大的γ> 1惩罚更深的节点（对应更复杂的函数）也更严格。正则化的程度可以通过λ或γ超参数来调整。

3.森林生长过程和权重校正过程可能有不同的L2正则化参数，在这里视情况而定。

树尺寸

RGF不需要在梯度下降决策树设置所需的树尺寸（tree size）参数（例如，树的数量，最大深度）。使用RGF时，每棵树的尺寸是由最小正则化损失自动确定的。我们所声明的是森林中叶子的最大数量和正则化参数（L1和L2）。

模型尺寸

由于RGF在模型/森林上执行完全纠正步骤，因此与需要较小学习率和大量估计量来产生较好结果的梯度下降算法不同，它可以训练相对简单的模型。

在Python中的实现

原始RGF的二元分类和回归的实现是由论文的作者Rie Johnson和Tong Zhang使用C ++完成的。由fukatani开发的使用Python做相同实现的最流行的封装甚至支持多分类。大部分实现基于MLWave的RGF包装。

超参数

我们来谈谈影响模型准确性或者训练速度的重要参数：

• max_leaf：当森林中的叶节点数量达到此值时，训练将终止。所以它应该足够大，以便在训练时能够获得一个好的模型，而较小的值则能让训练时间更短。


• loss：损失函数
  
  
  
  • LS：平方损失（(p-y)^2/2。
  
  
  • Expo：指数损失 exp（-py）。
  
  
  • Log：logistic损失日志 (1+exp(-py))。
  
  
  
  


• algorithm：
  
  
  
  • RGF：RGF和L2正则化的单叶模型。
  
  
  • RGF Opt：RGF+最小惩罚正则化。
  
  
  • RGF Sib：RGF+最小惩罚正则化+同层级零和约束（sum-to-zero sibling constraints）。
  
  
  
  


• reg_depth：必须小于1. 与algorithm =“RGF Opt”或“RGF Sib”一起使用。值越大惩罚较深节点越重。


• l2：用于控制L2正则化的程度。想要取得良好性能的关键。依靠数据决定合适的值。通常1，0.1或0.01都会取得好的结果，尽管存在指数损失（loss= Expo）和逻辑损失（loss= Log），但是一些数据需要较小的值，例如1e-10或1e-20。


• sl2：覆盖森林生长过程中的L2正则化参数λ。也就是说，如果指定它，权重修正过程使用λ，森林生长过程使用λg。如果省略，则不进行覆盖，在整个训练过程中都使用λ。在某些数据中使用λ/100效果不错


• test_interval：RGF进行权重的彻底的校正更新，在指定的间隔和训练结束时，对所有树的叶节点的权值进行更新。
  
  
  
  • 因此，如果保存250棵树的模型，，那么这250棵树只能用于测试250棵树的附加模型。如果我们在获得“k”树的时候停止训练，分配给“k”树的节点的权重将与500棵树中的第一棵“k”树完全不同。
  
  
  • 如果测试间隔为500，则每次新增500个叶节点，仿真结束训练，对模型进行测试或将其保存以供后续测试。
  
  
  
  


• normalize：如果开启，训练目标被归一化，以使平均值归零。

使用python包装进行训练和评估

让我们尝试RGF上的大卖场预测问题。

数据集下载：https://datahack.analyticsvidhya.com/contest/practice-problem-big-mart-sales-iii/

如果想要详细了解预处理的步骤可以访问下方链接。

预处理：https://www.analyticsvidhya.com/blog/2016/02/bigmart-sales-solution-top-20/

import pandas as pd

import numpy as np



#Read files:

train = pd.read_csv("Train_UWu5bXk.csv")

test = pd.read_csv("Test_u94Q5KV.csv")



train['source']='train'

test['source']='test'

data = pd.concat([train, test],ignore_index=True)



#Filter categorical variables

categorical_columns = [x for x in data.dtypes.index if data.dtypes[x]=='object']



#Exclude ID cols and source:

categorical_columns = [x for x in categorical_columns if x not in ['Item_Identifier','Outlet_Identifier','source']]



#Get the first two characters of ID:

data['Item_Type_Combined'] = data['Item_Identifier'].apply(lambda x: x[0:2])



#Rename them to more intuitive categories:

data['Item_Type_Combined'] = data['Item_Type_Combined'].map({'FD':'Food',

 'NC':'Non-Consumable',

 'DR':'Drinks'})



#Years

data['Outlet_Years'] = 2013 - data['Outlet_Establishment_Year']



#Change categories of low fat:

data['Item_Fat_Content'] = data['Item_Fat_Content'].replace({'LF':'Low Fat',

 'reg':'Regular',

 'low fat':'Low Fat'})



#Mark non-consumables as separate category in low_fat:

data.loc[data['Item_Type_Combined']=="Non-Consumable",'Item_Fat_Content'] = "Non-Edible"



#Fill missing values by a very large negative val

data.fillna(-9999,inplace = True)



#Import library:

from sklearn.preprocessing import LabelEncoder

le = LabelEncoder()



#New variable for outlet

data['Outlet'] = le.fit_transform(data['Outlet_Identifier'])

var_mod = ['Item_Fat_Content','Outlet_Location_Type','Outlet_Size','Item_Type_Combined','Outlet_Type','Outlet']

le = LabelEncoder()

for i in var_mod:

 data[i] = le.fit_transform(data[i].astype(str))



train_new = train.drop(['Item_Identifier','Outlet_Identifier','Item_Outlet_Sales'],axis=1)

test_new = test.drop(['Item_Identifier','Outlet_Identifier'],axis=1)

y_all = train['Item_Outlet_Sales']

一旦我们有了预处理的存储数据，我们就可以使用下面的命令导入RGF:

from rgf.sklearn import RGFRegressor

from sklearn.model_selection import GridSearchCV

为此设置的两个最重要的参数max_leaf和L2正则化。我们可以使用网格搜索来找出具有最佳交叉验证MSE的参数。

parameters = {'max_leaf':[1000,1200,1300,1400,1500,1600,1700,1800,1900,2000],

              'l2':[0.1,0.2,0.3],

              'min_samples_leaf':[5,10]}

clf = GridSearchCV(estimator=rgf,

                   param_grid=parameters,

                   scoring='neg_mean_squared_error',

                   n_jobs = -1,

                   cv = 3)

看起来我们试图匹配有太多叶节点的过于复杂的模型。高的正则化项高，max_leaf进行程度较低。让我们用更小的max_leaf做一个不同的网格搜索：

parameters = {'max_leaf':[100,200,300,400,500,800,900,1000],

 'algorithm':("RGF_Sib","RGF"),

 'l2':[0.1,0.2,0.3],

 'min_samples_leaf':[5,10]}

看起来像这些参数是最合适的。它在公共排行榜上RMSE的得分是1146。

总结

RGF是另一种树集成技术，它类似梯度下降算法，可用于有效建模非线性关系。