使用较少位的精度来训练机器学习模型是否会限制训练的准确性呢？这篇文章描述了一些情况，我们可以通过被称为位中心化（bit centering）的技术使用低精度计算获得高准确性的解（solution）。

低精度计算在机器学习中得到了广泛的应用。有些公司甚至已经开始开发新的硬件架构，这些架构本身支持和加速低精度操作，包括微软的Project Brainwave和Google的TPU。尽管使用低精度可以获得很多系统优势，但低精度方法主要用于推断，而不是训练。过去的低精度训练算法需要作出一种权衡：当计算使用较少的位时，会增加更多的舍入误差，从而限制了训练的准确性。根据传统观点，这种权衡限制了从业者在其系统中部署低精度训练算法。 但这种权衡真的是必须的吗？有没有可能设计一种算法，既可以使用低精度训练，又不会限制它的准确性？

事实证明，我们真的可以从低精度训练得到高准确性的解。在这里，我将介绍的随机梯度下降（SGD）的新变种，HALP（high-accuracy low precision，高准确性低精度 ），它可以做到这一点。HALP之所以优于以前的算法，是因为它减少了限制低精度SGD的精度的两个噪声源：梯度方差和舍入误差。

• 为了减少梯度方差的噪声，HALP使用了SVRG（stochastic variance-reduced gradient）技术。SVRG定期使用完全梯度来减少SGD中使用的梯度样本的方差。


• 从量化的数字为低精度表示降低噪声，HALP采用了全新的技术，我们称之为“bit centering”（位中心化）。位中心化的原理是，当我们接近最优时，梯度变小，从某种意义上说，携带的信息更少，所以我们应该能够对它进行压缩。通过动态地重新中心化并重新缩放我们的低精度数据，我们可以在算法收敛时降低量化噪声。

通过将这两种技术结合起来，HALP在与全精度SVRG相同的线性收敛速率下，生成任意准确的解，同时使用具有固定位数的低精度迭代。这一结果颠覆了传统上认为的，低精度的训练算法所能达到的效果。

为什么低精度SGD有限？

首先，设置好我们想要解决的问题：



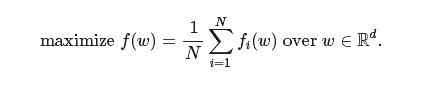
这是一个经典的经验风险最小化问题，可以用于训练许多机器学习模型（包括深度神经网络）。标准的解决方法是随机梯度下降法，它是一种迭代算法，通过运行下面的式子来达到最优。



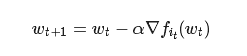
在这里i_t是在每次迭代从{ 1 ，... ，N }中随机选择的索引。我们想运行这样的算法，但要使迭代W_t低精度。也就是说，我们希望他们使用少量位（通常为8位或16位）的定点运算（这与这些算法标准的32位或64位浮点数相比要小）。但是，当它直接完成SGD更新规则时，我们遇到了表示问题：问题的解w^*在选定的定点表示法中可能无法表示。例如，如果我们使用可以存储整数的8位定点表示$\{$$-$$128$$，$$-$$127$$，$$...$$，$$127$$\}$，真正的解是w^*$=$$\mathrm{100.5，但}$不能真的有，因为我们不能表示非整数。除此之外，将梯度转换为定点导致的舍入误差可能会减慢收敛速度。这些效应限制了低精度SGD的准确性。

位中心化

当我们运行SGD时，从某种意义上说，我们实际上在做的是平均我们实际上在做的是平均（或总结）一堆梯度样本。位居中背后的关键思想是随着梯度变小，我们可以使用相同的位数以较小的误差对它们进行平均。为了进行说明，想想平均一串数字(- 100 ，100]并比较这对在平均一串数字(- 1 ，1 ]。在前一种情况下，我们就需要选择的定点表示要能覆盖整个区间(- 100 ，100 ]（例如，{ - 128， - 127，...，126，127}），而在后一种情况下，我们可以选择一个覆盖(- 1 ，1 ]范围的（例如，{-128/127，...，127/127}）。这意味着，具有固定数量的位，delta（德尔塔），相邻的可表示数之间的差异，后一种情况比前者更小，因此，舍入误差也会更低。

这个想法给了我们灵感。用比在区间$\mathrm{（}$在区间（- 1 ，1 ]的数字，我们需要使用不同的定点表示。这种表明我们应该动态地更新低精度表示法：随着梯度变小，我们使用的定点数的delta和区间也要变小。

但我们怎样知道如何更新我们的表示呢？我们需要覆盖哪些范围呢？如果我们的目标是参数μ的强凸（strongly convex），那么无论何时我们在某个点w上获得完整的梯度，我们可以限制下面公式的最佳的位置。



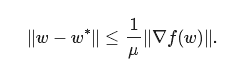
这种不等式为我们提供了可以找到解的值的范围，所以无论何时计算完整梯度，我们都可以重新中心化并重新缩放低精度表示以覆盖此范围。下图说明了该过程。



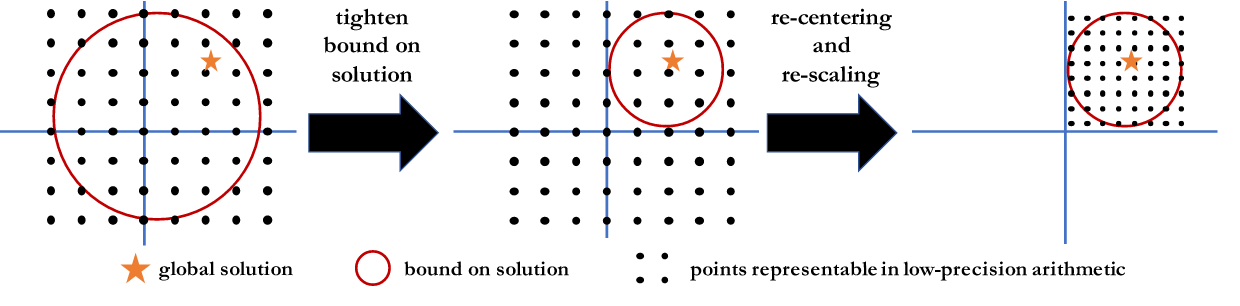
我们称这一操作位中心化（bit centering）。请注意，即使我们的目标不是强凸函数，也可以执行位中心化：现在参数$\mu$成为算法的超参数。随着周期性的位中心化，算法的收敛，量化误差会减小。事实证明，这种方法可以让它收敛到任意精确的解。

HALP

HALP是我们的算法，它运行SVRG并在每个周期（epoch ）使用具有完整梯度的位中心化来更新低精度表示。 在这里，我们只是简要介绍一下这些结果（细节请访问下方链接）。首先，我们证明了对于强凸的Lipschitz光滑函数（这是最初分析SVRG收敛速度的标准设置），只要我们使用的位数满足：



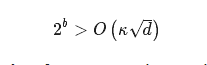
其中κ是问题的条件数（condition number），那么适当设置步长和周期（设置细节在论文中），HALP将使线性速率收敛到任意精确的解。也就是说，对于0 < γ < 1有：



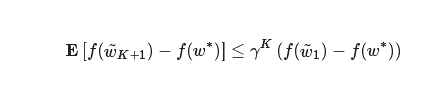
其中表示迭代了第K个周期。如下图所示：



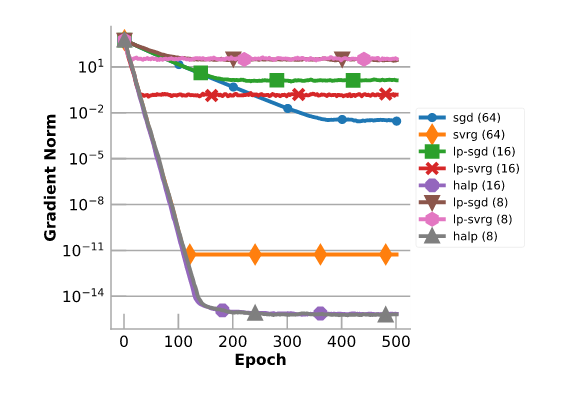
该图通过对具有100个特征和1000个示例的合成数据集进行线性回归来评估HALP。它将其与基础的全精度SGD和SVRG，低精度SGD（LP-SGD）以及没有使用位中心化的低精度的SVRG（LP-SVRG）进行比较。请注意，即使只有8位（尽管最终受到浮点数误差的限制），HALP仍能收敛到非常高准确性的解。在这种情况下，HALP收敛到比全精度SVRG更高准确性的解，由于HALP使用较少的浮点运算，因此对浮点不准确性较不敏感。

论文的其他结果：

• 我们展示了HALP匹配SVRG的收敛轨迹 - 即使对于深度学习模型也是如此。


• 我们有效地实施了HALP，并且它可以比CPU上的全精度SVRG快4倍。


• 我们还在深度学习库TensorQuant中实施了HALP，并发现它可以在一些深度学习任务中超过普通低精度SGD的验证性能。

显然，下一步是在低精度硬件上高效实现HALP。

论文：http://www.cs.cornell.edu/~cdesa/papers/arxiv2018_lpsvrg.pdf