您尚未登录账户请先登录您的atyun账户，方可使用该功能
您的企业账号申请正在审核中审核通过后即可使用此功能，请耐心等待~
一文教你如何正确利用kNN进行机器学习
2018年03月16日 由 xiaoshan.xiang 发表
832905
0
k最近邻算法（kNN）是机器学习中最简单的分类方法之一，并且是入门机器学习和分类的好方法。它基本上是通过在训练数据中找到最相似的数据点进行分类，并根据分类做出有根据的猜测。理解和实现起来非常简单，所以这种方法在很多领域都有广泛的应用，例如推荐系统，语义搜索和异常检测。
正如我们在任何机器学习问题中所需要的一样，我们必须首先找到一种方法来将数据点表示为特征向量。特征向量是我们的数据的数学表示，由于我们的数据的期望特征可能不是固有的数值，所以可能需要预处理和特征工程来创建这些向量。给定的数据带有N个独特的特征,特征向量将是长度为N的向量，其中向量的入口I表示特征I的数据点值。因此，每个特征向量可以被认为是R ^ N中的点。
与大多数其他分类方法不同，kNN属于惰性学习，这意味着在分类之前没有明确的训练阶段。相反，任何对数据进行概括或抽象的尝试都是在分类时进行的。这意味着一旦我们有了数据，就可以立即开始分类，但这类算法存在一些固有的问题。我们必须能够将整个训练集保存在内存中，除非我们对数据集应用某种类型的简化（reduction），并且执行分类可能在计算上耗费巨大，因为算法通过每个分类的所有数据点进行解析。由于这些原因，kNN往往适用于特征不多的小型数据集。
一旦我们形成了我们的训练数据集，将其表示为M×N矩阵，其中M是数据点的数量，N是特征的数量，我们现在可以开始分类。对于每个分类查询，kNN方法的要点是：
1.计算要分类的项目与训练数据集中的每个项目之间的距离值
2.选取k个最近的数据点（k个最小距离的项目）
3.在这些数据点之间进行“多数票决” - 该池中的主要分类被确定为最终分类
在进行分类前必须做出两项重要决定。一个是将要使用的k的值; 这可以随意选择，也可以尝试交叉验证以找到最佳值。接下来最复杂的是将要使用的距离度量。
有很多不同的方法来计算距离，因为它是一个相当模糊的概念，并且适当的度量总是由数据集和分类任务决定。两种最流行的方法是欧几里得距离和余弦相似度。
欧几里德距离可能是你最熟悉的那个; 它基本上是通过从待分类点中减去训练数据点而获得的向量的大小。
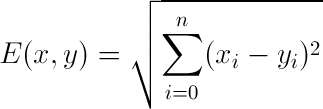
欧几里得距离的一般公式
另一个常见的度量是余弦相似度。与计算大小不同，余弦相似度利用了两个向量之间的方向差异。
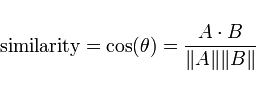
余弦相似度的一般公式
选择度量标准通常会非常棘手，最好使用交叉验证来决定，除非你清楚地知道你正在使用的比其他的要好。例如，对于像词向量之类的东西，你可能想要使用余弦相似度，因为词的方向比分量值的大小更有意义。一般来说，这两种方法运行时间大致相同，并且会受到高维数据的影响。
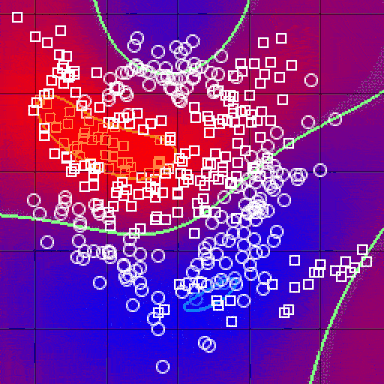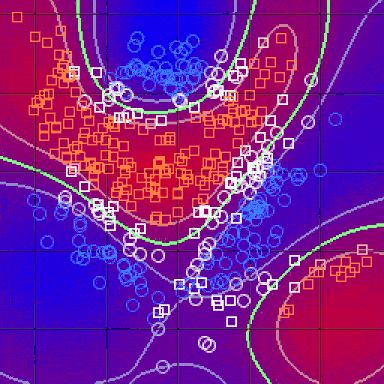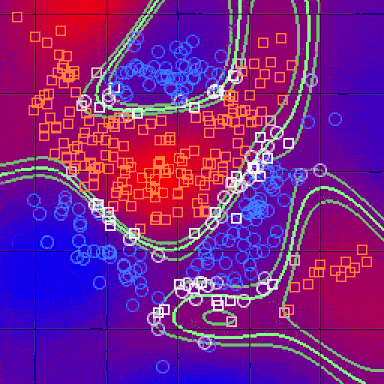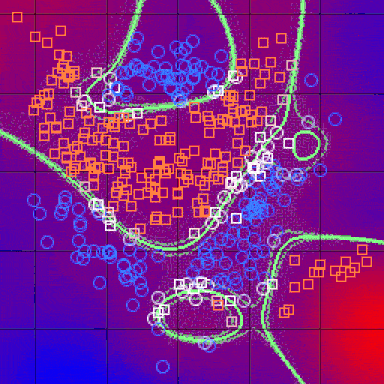
在完成上述所有步骤并确定度量之后，kNN算法的结果是将R ^ N划分为多个部分的决策边界。每个部分（在下面明显着色）表示分类问题中的一个类。边界不需要由实际的训练样例形成 - 而是使用距离度量和可用的训练点来计算边界。通过在（小）块中获得R ^ N，我们可以计算出该区域内假设数据点的最可能类，因此我们将该块的颜色标记为该类的区域。
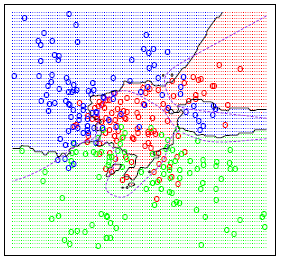
这个信息是开始实现这个算法所需要的，这样做应该相对简单。当然，有很多方法可以改进这个基本算法。常见的修改包括加权和特定的预处理，以减少计算和减少噪声，例如各种用于特征提取和降维的算法。此外，kNN方法也被用于回归任务，虽然不太常见，但它的操作方式与均值分类器非常相似。
欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
广告
广告
写评论取消
回复取消