如果你打算从UC Berkeley骑行到金门大桥（Golden Gate Bridge），这样骑行20英里也不错，但问题是，你从没骑过自行车！更棘手的是，你初来乍到，对这里还不熟，手里只有一份OL的时尚地图，那么你要怎么做？

首先来解决如何学会骑自行车的问题。其中一个方法是进行大量研究和计划，阅读关于骑行的书籍，研究物理学和解剖学，探索每次动作时你需要做出的不同的肌肉运动，等等。这种方法看似可行，然而骑过自行车的人都知道这种方法只是纸上谈兵。只有一种方法可行，那就是试错。像骑行这样的任务太过复杂，空想计划是不可行的。

一旦你学会了骑行，那么要怎样到达目的地呢？你可以再次利用试错法，随机进行转弯看是否能抵达Golden Gate Bridge，然而这一方法需要花费太多时间。对这样的问题来说，计划则速度更快，不需太多的实际经验和试错。用强化学习的术语来表达就是sample-efficient。

通过试错法学习技巧

其他情况，事先计划好会更好

这个想法虽然简单，但强调了人类智能的一些重要方面。对于某些任务，我们使用试错法，而对于其他任务，我们使用的是计划法。在强化学习（RL）中也出现了类似的现象。用RL的术语来说，就是实证结果表明，一些任务更适合model-free（试错）方法，而另一些则更适合model-based（计划）方法。

然而，用骑行进行类比也强调了这两个系统并不是完全独立的。学习骑行就是试错，这种说法太过夸张。事实上，当你通过试错法来学习骑车时，你也会采取一些计划。也许最初的计划是“不要摔倒”。当你更熟练之后，你会设立更高的目标，比如“向前骑两米不摔倒”。最终，你精通了骑行技巧，然后开始设定抽象的计划（骑到这条路的尽头），这样你只需要不断计划，而无需再拘泥于骑行的细节。这一过程便是从model-free（试错）策略到model-based（计划）策略的逐步过渡。如果我们通过开发人工智能算法，特别是RL算法，来模拟这种行为，那么可能会产生一种算法，既能通过早期使用试误法较好地完成任务，又能在之后转换到计划法来实现更抽象的目标，体现sample efficient。

这篇文章会用到temporal difference model（TDM），是一种RL算法，可以将model-free平稳过渡到model-based RL。在描述TDM之前，我们先来看看典型的基于模型的RL算法是如何工作的。

model-based RL

在强化学习中，存在许多状态空间S和动作空间A。如果时间是t，那么我们所处的状态和采取的动作分别用st∈S和at∈A来表示，根据动态模型f:S×A↦S，我们转换到新的状态就可表示为st+1=f(st,at) 。目标是最大化已有状态总结的回报：∑T−1t=1r(st,a,st+1)。model-based RL算法假设你已得到得到（或学会）动力模型f。根据这一模型，可用各种model-based算法。在这篇文章中，我们执行以下的optimization方法，以选择一系列动作和状态，使回报最大化。



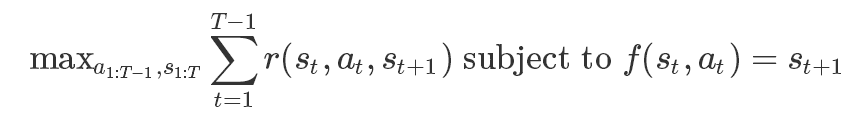
optimization方法选择一系列动作和状态，使回报最大化，同时确保轨迹是可行的。在这里，可行的意思是状态与动作直到下一个状态的转化都有效。例如下面的图片，如果你从状态st和动作at开始，只有最上一列的st+1会使转化可行。



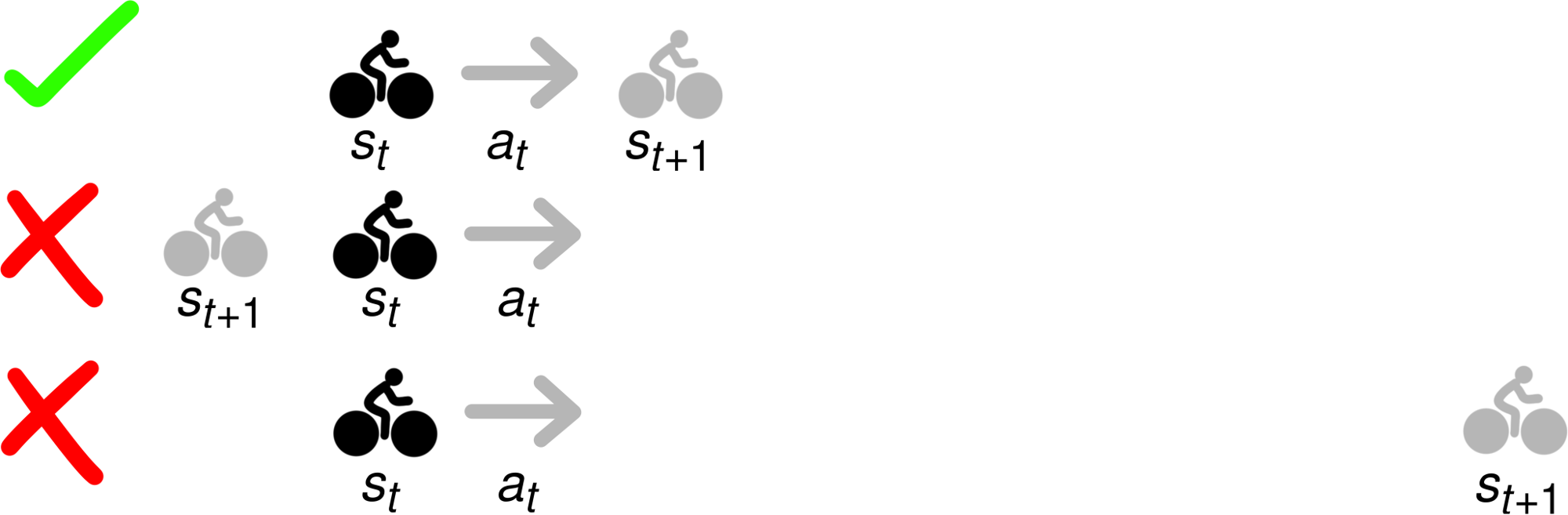
如果你忽略掉物理学，计划骑行到Golden Gate Bridge会更简单些。然而，model-based最优化的问题约束确保仅有的轨迹（如最上一列）可被输出。下面两列轨迹可能会得到高回报，不过都是不可行的。

在我们的自行车问题中，最优化可能会使从Berkeley（右上）到Golden Gate Bridge（中左）的骑行计划看起来如下图：

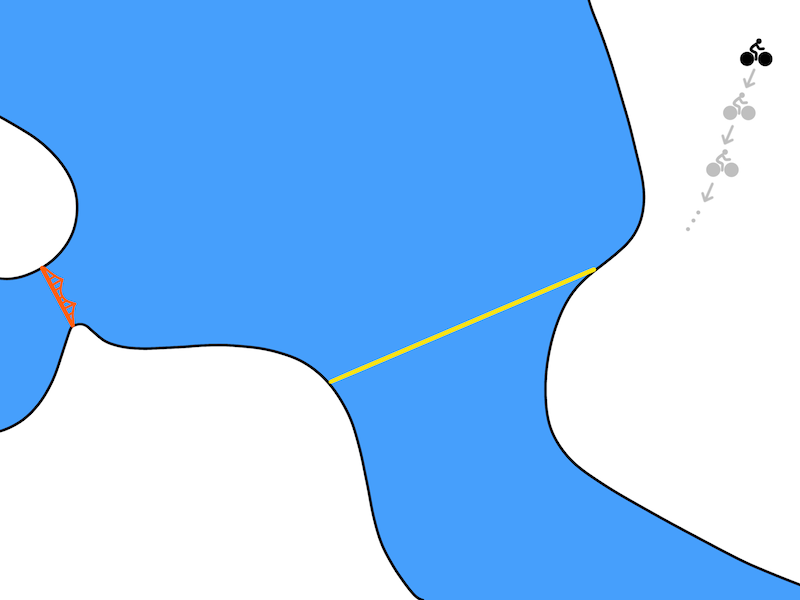
Optimization问题的计划（状态和动作）输出实例

虽然理念很好，但这个计划并不现实。model-based方法利用模型f(s,a)预测接下来的每一个状态。在机器人学中，时间步长通常对应十分之一秒或百分之一秒。所以一个更现实的计划可能如下图所示：

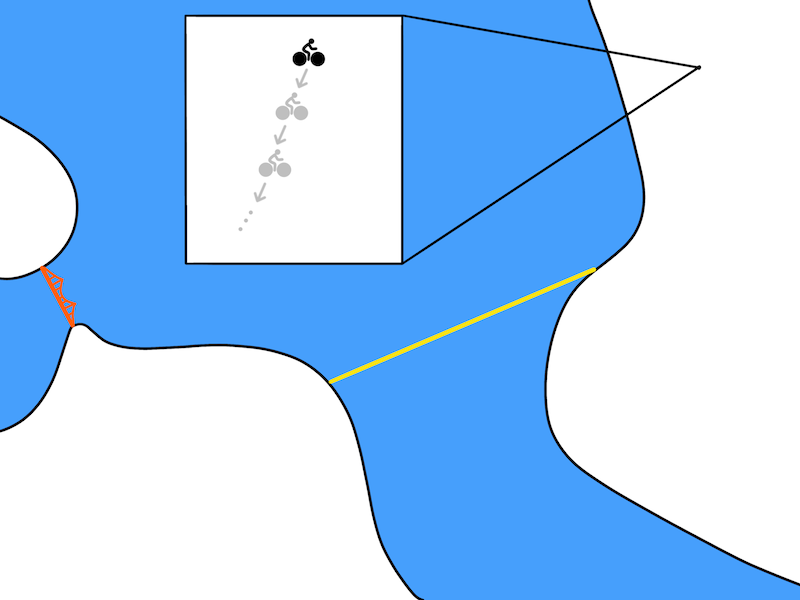
一个更为现实的计划

如果思考一下我们在日常生活中是如何计划的，就会意识到我们会用更多时间计划抽象术语。我们会制定长期计划如“我要骑到这条路的尽头”，而不是计划在下个十分之一秒具体骑到哪个位置。此外，一旦学会如何骑行，我们就只会做这些抽象的计划。正如上文所讨论的那样，我们需要一些方法，用来(1)通过试错法开展学习，(2)提供一种机制，逐步提高我们用于计划的抽象级别。为了实现这些，我们引进了temporal difference model。

TDM

我们将TDM写作Q(s,a,sg,τ)*，这是一个函数，我们所处的状态和采取给定状态为st∈S，动作为at∈A，目标状态为sg∈S，以此预测智能体如何在τ 长度的时间步长内完成目标。也就是说用TDM来回答“如果我想在30分钟内骑行到San Francisco，我能距离终点多远？”对于机器人学来说，一个测量接近程度的方法就是Euclidean distance。

*我们称它为temporal difference model，因为我们用时间差异学习来训练Q，并使用Q作为模型。



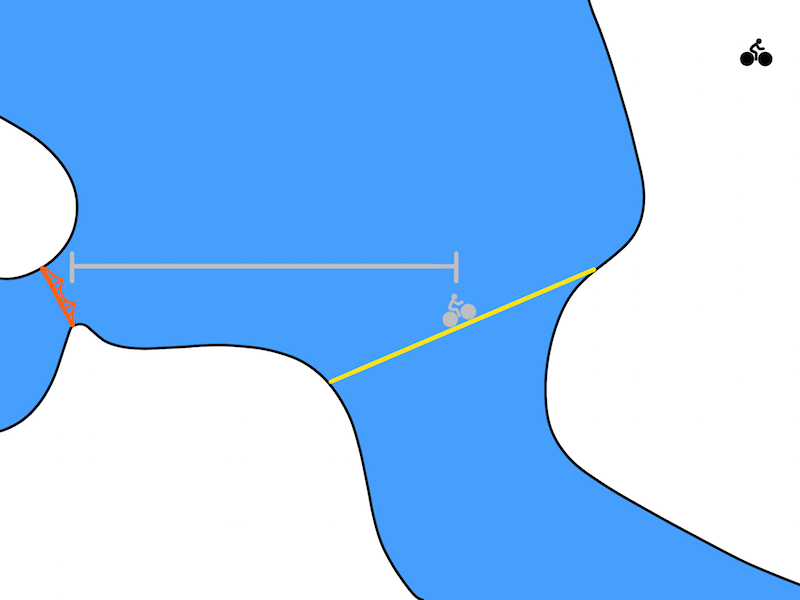
经过固定的时间后，TDM预测你离目的地的距离（Golden Gate Bridge）。骑行30分钟，也许你只能到达上图中灰色自行车的位置。在这种情况下，灰线代表TDM应该预测的距离。

对于那些熟悉强化学习的人来说，在finite-horizon MDP中，TDM可以被视为一个目标已定的Q函数。因为TDM也是Q函数，我们可以用model-free（试错法）算法训练它。我们用deep deterministic policy gradient（DDPG）来训练TDM，并对目标和时间范围进行追溯并重新标记，以提高我们学习算法的sample efficiency。理论上，任何Q-learning算法都可用于训练TDM，不过我们发现这种最有效率。

用TDM制定计划

一旦我们训练了TDM，那我们如何将它用于制定计划？我们可以根据以下的optimization来制定计划：



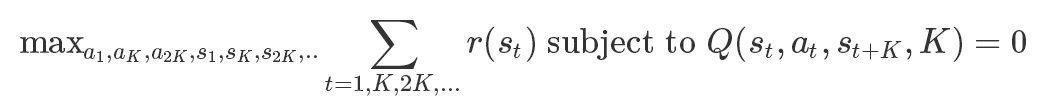
这类似于model-based的构想。选择一系列使回报最大化且可行的动作和状态。关键差异在于我们只能每k个时间步长计划一次，而不是每个时间步长都计划一次。Q(st,at,st+K,K)=0中存在的约束强制了轨道的可行性。视觉上来说并不是明确计划K步以及如下动作：



而是直接计划K个时间步长，如下图：



随着K的增加，我们逐渐得到越来越多暂时的抽象计划。在K时间步长中，我们用model-free approach采取行动，从而使model-free策略将如何达到终点的细节抽象化。对于骑行问题以及足够大的K值，通过optimization可以得到如图所示的计划：



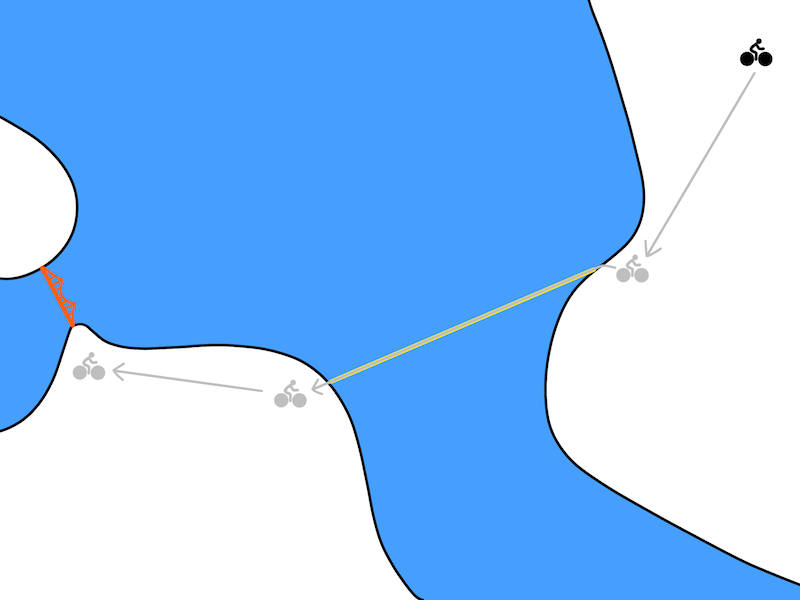
model-free计划者可用于选择暂时的抽象目标。可以用model-free算法来实现这些目标。

需要注意的是，这一构想只能每K步优化一次回报。然而，许多任务只考虑某一些状态，比如最终状态（如抵达Golden Gate Bridge），而这一点正适用于各种有趣的任务。

相关研究

在我们之前已有人对model-based和model-free之间的联系进行了研究。Parr ‘08和Boyan ‘99与此研究密切相关，虽然重点只是tabular函数和linear函数approximators。训练目标条件Q函数的想法，是从关于智能体导航和Atari游戏的研究——Sutton ‘11和Schaul ‘15中提取的。最近，我们使用的重新标记的方法是受到了Andrychowicz ‘17研究的启发。

实验

我们用5个模拟的连续控制任务和一个真实的机器人任务测试了TDM。模拟任务是训练机械手臂将圆柱体推到目标位置。下面的示例展示了最终采用的TDM策略以及相关的学习曲线：

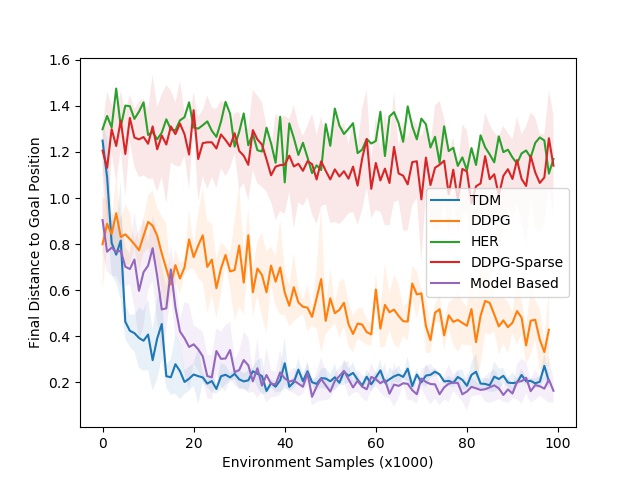
上图：任务的TDM策略 下图：学习曲线 蓝线代表TDM（线的位置越低越好）

在学习曲线中，我们画出到目标的最终的距离以及环境样本的数量（越低越好）。我们的模拟将机器人控制在20赫兹，这意味着在现实世界中，50秒对应1千步。这种环境的动态相对容易学习，这意味着model-based的方法应该更胜一筹。正如预期，model-based方法（紫色的线）学习速度更快，大约3千步或者说25分钟，而且表现也很好。TDM方法（蓝色曲线）学习速度也很快，大约2千步，17分钟。model-free DDPG（没有TDM参与）基线最终解决了问题，但是需要更多的训练样本。TDM方法学习如此之快的一个原因是，其效果相当于套用了model-based方法。

当涉及更需要大量动力的移动任务时，model-free方法的优势就明显多了。其中一项移动任务是训练一个四足机器人，让它移动到一个特定的位置。下图展示了TDM策略与其学习曲线。

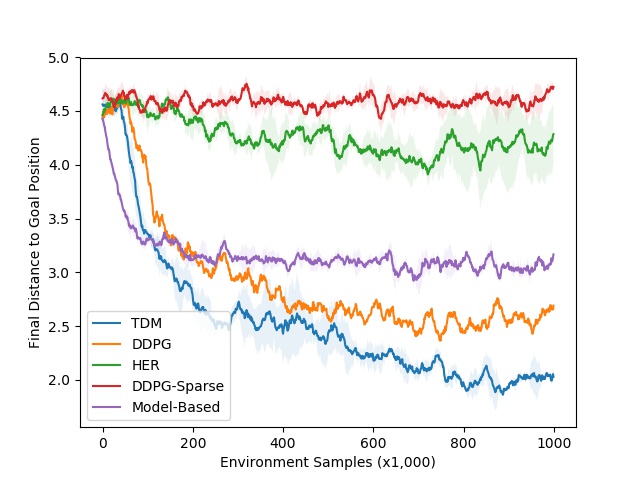
上图：移动任务的TDM策略 下图：学习曲线 蓝线代表TDM（线的位置越低越好）

就像我们使用试错法而不是计划去学习骑自行车，我们期望model-free方法在移动任务上比model-based方法表现更好。这正是我们在学习曲线中看到的：model-based方法表现更好。model-free DDPG方法学习速度更慢，但是最终还是胜过了model-based方法。TDM则速度又快表现又好。

未来发展方向

TDM为model-free到model-based控制的转换，提供了形式主义和实用算法。然而，未来还有很多研究要做。比如，推导假定环境和政策是确定的。事实上，大多数环境都是随机的。即使它们是确定的，在现实中还是有必须使用随机政策的理由。TDM扩展到这一设定有助于将TDM迁移到更实际的环境中。另一个想法是将TDM与我们在文中使用的model-based planning optimization算法结合起来。最后，我们很期待将TDM与现实中的机器人结合，应用到更多有挑战性的任务中，比如移动任务，操纵任务，当然也包括骑行到Golden Gate Bridge任务。