利用协方差,Pearson相关系数和Spearman相关系数确定变量间的关系
2018年05月02日 由 浅浅 发表
671543
0
数据集中的变量之间可能存在复杂且未知的关系。重要的是发现和量化数据集的变量相关的程度。这些知识可以帮你更好地准备数据,以满足机器学习算法的预期,例如线性回归,其性能会随着这些相关的出现而降低。
在本教程中,你会了解到相关性是变量之间关系的统计概要,以及在不同类型的变量和关系中,如何计算它。
学完本教程,你会明白:
- 如何通过计算协方差矩阵,总结两个或多个变量间的线性关系。
- 如何通过计算Pearson相关系数,总结两个变量间的线性关系。
- 如何通过计算Spearman相关系数,总结两个变量之间的单调关系(monotonic relationship)。
教程概述
本片教程分为5个部分,分别是:
- 什么是相关
- 测试数据集
- 协方差
- Pearson相关
- Spearman相关
什么是相关
有很多原因会使数据集内的变量之间存在相关关系。
例如:
- 一个变量可能决定或取决于另一个变量的值。
- 一个变量很容易与另一个变量有关联。
- 两个变量可能取决于第三个未知变量。
这在数据分析和建模中很有用,可以更好地理解变量间的关系。两个变量之间的关系在统计学中叫做“相关”。相关可能为正,意味着两个变量都在同一方向上移动,也可能为负,意味着当一个变量值增加时,另一个变量的值就会减少。相关也可能为零,也就是说这些变量是不相关的。
- 正相关:两个变量都在同一方向上变化
- 零相关:变量间的变化不存在相关
- 负相关:变量在相反的方向变化
如果两个或两个以上的变量紧密相关,即多重共线性,那么一些算法的性能就会下降。例如线性回归,为了提高模型的技能,应该移除其中有干扰的相关变量。我们可能还会对输入变量与输出变量间的相关感兴趣,因为这些在开发模型输入中,可以用来判断哪些变量会有相关性。
关系的结构可能是已知的,例如它可能是线性的,或者我们也可能不知道两个变量间是否存在关系,以及可能采用的结构。根据已知的关系和变量的分布情况,可以计算出不同的相关分数。
在本教程中,我们将探索一个符合高斯分布和线性关系的变量的分数,而另一个则不假定分布,并且会报告所有单调(增加或减少)关系。
测试数据集
在我们研究相关方法之前,让我们定义一个用来测试那些方法的数据集。我们生成1000个成对变量样本,并且它们之间具有很强的正相关。第一个变量是从平均数100、标准差20的高斯分布中抽取的随机数。第二个是第一个变量的值,加上平均数为50、标准差为10的高斯噪声。
使用randn()函数来生成随机的高斯值(高斯分布的平均值为0,标准差为1),然后用我们自己的标准差乘以结果,并加上平均数,将值变换到你想要的范围。使用伪随机数生成器,以确保每次运行代码时都得到相同的数字样本。
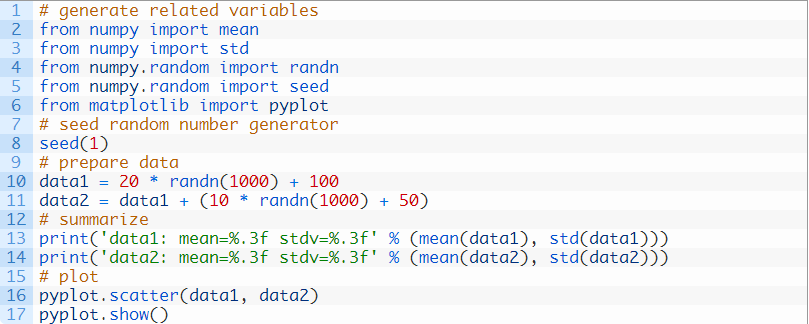
运行这个示例,首先打印每个变量的平均数和标准差。
创建两个变量的散点图。因为我们是自己建立了数据集,我们知道这两个变量间存在关系。当我们查看散点图时,很明显能看出递增的趋势。
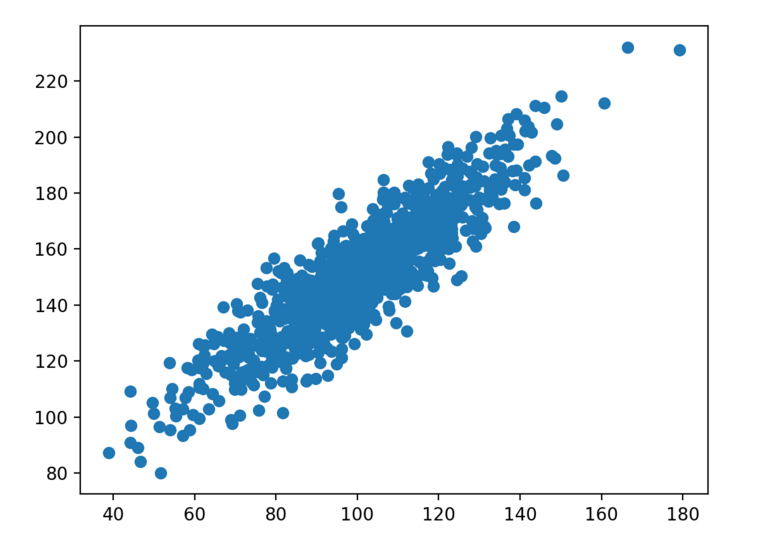
测试相关数据集的散点图
在我们计算相关分数之前,我们首先要考虑一个重要的统计方法——协方差。
协方差
变量之间可能会存在线性关系。这种关系在两个数据样本中递增一致。这种关系在两个变量之间被称为协方差。它是根据每个样本值之间的平均值乘积来计算的,其中这些值都要分别减去平均值。
计算样本协方差:
在计算中使用平均值表明,每个数据样本都要符合高斯或类高斯分布。可以通过两个变量是否一起增加(正)或一起减少(负),来解释协方差。很难解释协方差的大小。协方差值为0表明这两个变量都是完全独立的。
cov()NumPy函数可用于计算两个或多个变量间的协方差矩阵。
矩阵的主对角线包含每个变量和它本身之间的协方差。矩阵中的其他值表示两个变量之间的协方差;在这种情况下,余下的两个值是相同的,因为我们只计算两个变量的协方差。
我们可以计算出测试问题中两个变量的协方差矩阵。
下面列出了完整的示例。
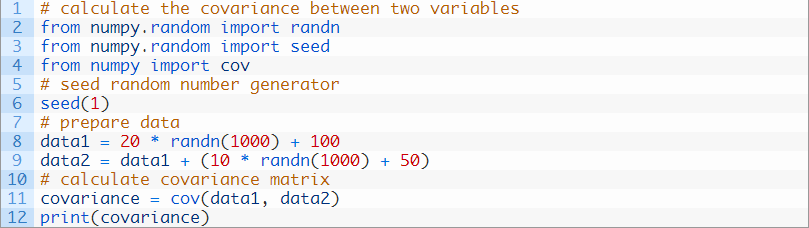
协方差和协方差矩阵在统计学和多元分析中应用广泛,主要用于描述两个或多个变量之间的关系。运行这个示例,计算并打印协方差矩阵。
因为每个变量是从高斯分布抽取,并具有线性相关,数据集是由这些变量人为建立的,所以协方差对于描述关系来说是很合适的方法。这两个变量之间的协方差是389.75。我们可以看到它是正向的,即正相关。
单独使用协方差这一统计工具的问题是,解释结果并不容易。所以下面我们来介绍Pearson相关系数。
Pearson相关
Pearson相关系数可用来总结两个数据样本之间线性关系的强度。计算Pearson相关系数是用两个变量的协方差除以每个数据样本标准差的乘积。这是两个变量之间协方差的标准化,从中可以得出一个可解释的分数。
在计算中使用平均值和标准差表明,两个数据样本需要符合高斯或类高斯分布。计算的结果,即相关系数可以被解释,并用于理解其间关系。
该系数返回的值在-1到1之间,表示相关的范围,即从完全负相关到完全正相关。0表示无相关。这个值必须被解释,通常低于-0.5或高于0.5的值表示显著的相关,其他范围的值则表示相关不显著。
pearsonr() SciPy函数可以计算两个相同长度的数据样本的Pearson相关系数。我们可以计算出测试问题中两个变量间的相关。
下面列出了完整的示例。
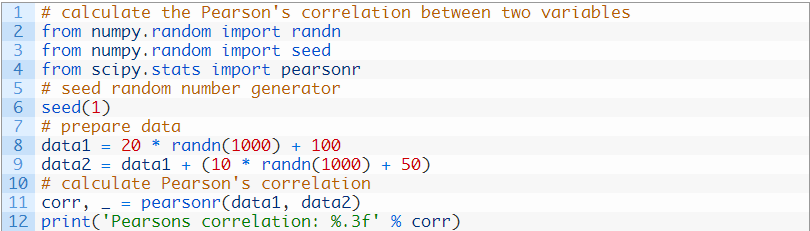
运行这个示例,计算并打印出Pearson相关系数。
我们可以看到这两个变量存在正相关关系,相关性为0.8。这意味着高相关,因为高于0.5且接近1.0。
可以用Pearson相关系数来评估两个以上变量间的关系。
这可以通过计算数据集中每一对变量之间关系的矩阵来实现。
结果是对称矩阵,被称为相关矩阵,因为主对角线上的值是1.0,每一列总与其自身完全相关。
Spearman相关
两个变量可能有非线性关系,那么这一关系强度可能随着变量分布变化。此外,这两个变量可能是非高斯分布。在这种情况下,Spearman相关系数可用来总结两个数据样本的关系强度。这个方法也能判断变量间的线性关系,不过检验效能稍弱(可能相关分数会比正常更低)。
与Pearson相关系数一样,Spearman相关系数用-1到1表示相关的范围,即从完全负相关到完全正相关。这些统计数据是用每个样本中值的相对秩计算出来的,而并非用样本本身的协方差和标准差。这是一种常用的非参数统计方法,例如,我们不假定数据分布为高斯分布时,我们就使用这种统计方法。
尽管假定为单调关系,但变量之间的线性关系没有被假定。用单调关系可以描述两个变量之间增加或减少的关系。
如果你不确定两个变量之间的分布和可能存在的关系,那么用Spearman相关系数很合适。用spearmanr() SciPy函数计算两个相同长度的数据样本的Spearman相关系数。我们可以计算出测试问题中两个变量间的相关。
下面列出了完整的示例。
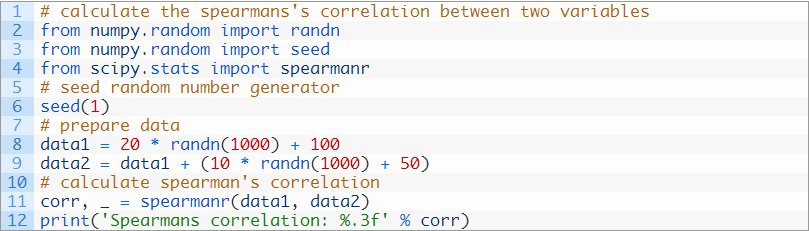
运行这个示例,计算并打印出Spearman相关系数。
我们可以看到数据符合高斯分布且变量之间存在线性相关。然而,非参数秩次方法显示了变量间的高相关,相关为0.8。
与Pearson相关系数相同,Spearman相关系数可以成对计算数据集中的系数并得出相关矩阵。
扩展
本节列出了一些本教程的想法扩展,你可能希望进行深入探索。
- 用正、负相关生成你自己的数据集,并计算相关系数。
- 编写函数计算数据集的皮尔逊或斯皮尔曼相关矩阵。
- 建立一个标准的机器学习数据集,并计算所有实值变量对的相关系数。
总结
读完本教程,你明白了相关性是变量之间关系的统计概要,以及在不同类型的变量和关系中,如何计算它。
具体来说,你学会了:
- 如何通过计算协方差矩阵,总结两个或多个变量间的线性关系。
- 如何通过计算Pearson相关系数,总结两个变量间的线性关系。
- 如何通过计算Spearman相关系数,总结两个变量之间的单调关系。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























