Adam优化算法是一种对随机梯度下降法的扩展，最近在计算机视觉和自然语言处理中广泛应用于深度学习应用。在引入该算法时，OpenAI的Diederik Kingma和多伦多大学的Jimmy Ba在他们的2015 ICLR发表了一篇名为“Adam: A Method for Stochastic Optimization”的论文，列出了使用亚当在非凸优化问题上的诱人好处，如下:

• 简单直接的实施


• 计算上讲究效率


• 小内存要求


• 不变量对梯度的对角线重新调节


• 非常适合于数据和/或参数方面的问题


• 适合非平稳的目标


• 适用于非常稀梳梯度的问题。


• 超参数具有直观的解释，通常需要很少的调谐。

Adam如何工作？

Adam与经典的随机梯度下降法是不同的。随机梯度下降保持一个单一的学习速率(称为alpha)，用于所有的权重更新，并且在训练过程中学习速率不会改变。每一个网络权重(参数)都保持一个学习速率，并随着学习的展开而单独地进行调整。该方法从梯度的第一次和第二次矩的预算来计算不同参数的自适应学习速率。

作者描述Adam时将随机梯度下降法两种扩展的优势结合在一起。

具体地说:

自适应梯度算法(AdaGrad)维护一个参数的学习速率，可以提高在稀疏梯度问题上的性能(例如，自然语言和计算机视觉问题)。

均方根传播(RMSProp)也维护每个参数的学习速率，根据最近的权重梯度的平均值(例如变化的速度)来调整。这意味着该算法在线上和非平稳问题上表现良好(如:噪声)。

Adam意识到AdaGrad和RMSProp的好处。与在RMSProp中基于平均第一个时刻(平均值)的参数学习速率不同，Adam也使用了梯度的第二个时刻的平均值(非中心方差)。

具体地说，该算法计算了梯度和平方梯度的指数移动平均值，并且参数beta1和beta2控制了这些移动平均的衰减率。移动平均值和beta1和beta2的初始值接近1.0(推荐值)，这导致了估计时间的偏差为0。这种偏差是通过第一次计算偏差估计然后再计算比可用偏差校正估计来克服的。

Adam是有效的

Adam在深度学习领域是一种很受欢迎的算法，因为它能很快取得好的成果。实证结果表明：在实践中，Adam的工作表现良好，并优于其他随机优化方法。

在原论文中，通过实证证明了该方法的收敛性满足了理论分析的期望。

在MNIST的字符识别和IMDB情绪分析数据集上，Adam采用了逻辑回归算法，对MNIST的数据集进行了多层感知器算法，并在CIFAR-10图像识别数据集上进行了卷积神经网络。

他们的结论是:

  “利用大型模型和数据集，我们证明了Adam可以有效地解决实际的深度学习问题。”

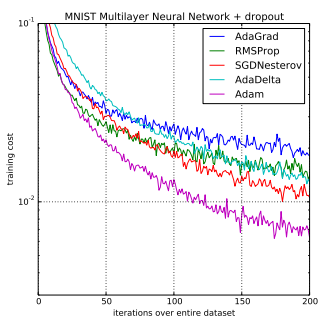
在斯坦福大学关于计算机视觉的深度学习课程中，Andrej Karpathy等人开发了一种名为“CS231n:卷积神经网络”的课程，这是一种被认为是深度学习应用的默认优化方法。

在实践中，Adam被推荐为使用的默认算法，并且通常比RMSProp稍微好一点。然而，作为一种替代方法，SGD+Nesterov Momentum也值得尝试。

Adam配置参数

• alpha也被称为学习速率或步长。权重比例被校正(例如001)。更大的值(例如0.3)在速率校正之前会加快初始学习速度。较小的值(例如1.0e-5)在培训期间降低学习速度


• beta1。第一次估计的指数衰减率(如9)。


• beta2。第二次估计的指数衰次减率(例如999)。在稀疏梯度问题(例如NLP和计算机视觉问题)上，这个值应该接近1.0。


• epsilon是一个非常小的数字，可以防止任何在实施中被0划分(例如，10e-8)。

最后，这里推荐一些比较受欢迎的使用默认参数的深度学习库：

• TensorFlow: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08.
  Keras: lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0.


• Blocks: learning_rate=0.002, beta1=0.9, beta2=0.999, epsilon=1e-08, decay_factor=1.


• Lasagne: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08


• Caffe: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08


• MxNet: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8


• Torch: learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8

 

此文为编译作品，作者为Jason Brownlee，详细内容参加原网站http://machinelearningmastery.com/adam-optimization-algorithm-for-deep-learning/