如何计算McNemar检验,比较两种机器学习分类器
2018年07月27日 由 yuxiangyu 发表
945160
0
统计假设检验的选择是解释机器学习结果的一个具有挑战性的开放问题。
在1998年被广泛引用的论文中,Thomas Dietterich在训练多份分类器模型副本昂贵而且不切实际的情况下推荐了McNemar检验。
它描述了深度学习模型的现状,模型非常大并且在大型数据集上进行训练和评估,一个模型通常需要数天或数周来训练。
在本教程中,你将了解如何使用McNemar统计假设检验来比较单个测试数据集上的机器学习分类模型。
完成本教程后,你将了解:
让我们开始吧。

本教程分为五个部分; 他们是:
Thomas Dietterich在他1998年发表的一篇重要的、被广泛引用的论文中,讨论了如何利用统计假设检验来比较分类器,论文“Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms”。链接:https://www.mitpressjournals.org/doi/abs/10.1162/089976698300017197
具体来说,当被比较的算法只能进行一次评估时推荐使用该检验,例如在一个测试集上,而不是通过重采样技术反复评估,例如k折交叉验证。
-Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
具体来说,Dietterich的研究涉及不同统计假设检验的评估,其中一些检验使用了重采样方法的结果。研究的关注点是低的第一类错误,即统计检验报告了为有影响实际上没有(假阳性)。
统计检验可以比较基于单一测试集的模型,这对现代机器学习来说十分重要,特别是在深度学习领域。
深度学习模型通常本身就很大,并且在非常大的数据集上运行。总之,这些因素可能意味着在现代硬件上对模型的训练可能需要数天甚至数周时间。
这排除了用重新采样方法比较模型的实际应用,并暗示了需要使用可以在单个测试数据集上评估训练模型结果的检验。
McNemar检验适合评估这些大型的、训练慢的深度学习模型。
McNemar检验基于列联表运行。在我们深入了解这种检验之前,让我们花点时间来理解如何计算两个分类器的列联表。
列联表是两个分类变量的制表或者说计数。在McNemar检验的情况下,我们对二元变量的正确/不正确(或者是/否)的控制和处理感兴趣(或者两种都有)。这被称为2×2列联表。
列联表乍一看可能并不直观。让我们做一个具体的例子。
我们有两个训练好的分类器。每个分类器对测试数据集中的10个实例中的每个实例进行二元分类预测。预测被评估并确定为正确的或不正确的(yes/no)。
然后我们可以在表格中汇总这些结果,如下所示:
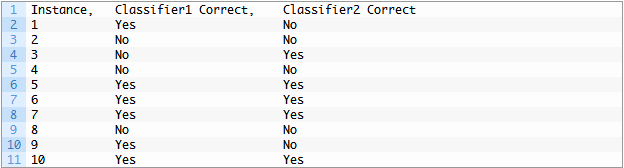
我们可以看到Classifier1得到6个Yes,或者说准确率为60%,Classifier2得到5个Yes,或者在测试集上有50%的准确率。
该表现在可以简化为列联表。
列联表依赖于这样一个事实 — 两个分类器都在完全相同的训练数据上训练并在完全相同的测试数据上进行评估。
列联表具有以下结构:
对于表中第一个单元格的情况,我们必须总结Classifier1得到正确且Classifier2也得到正确的检验实例的总数。例如,两个分类器正确预测的第一个实例是实例5.两个分类器正确预测的实例总数为4。
考虑到这点,另一种更具编程性的方法是在上面的结果表中对“是/否”的每个组合求和。
结果如下:
McNemar检验是配对的非参数或无分布统计假设检验。
它也不像其他一些统计假设检验那么直观。
McNemar检验是检查两个案例之间的分歧是否匹配。从技术上讲,这被称为列联表的同质性(homogeneity ,特别是边际同质性)。因此,McNema检验是一种列联表的同质性检验。
这个检验广泛用于医学领域,可以比较治疗对照的效果。
在比较两个二元分类算法时,检验是这两个模型是否存在相同的分歧的说明。它不会说明一个模型是否比另一个模型更准确或更容易出错。当我们看统计数据是如何计算的时候,这一点是显而易见的。
McNemar检验统计量的计算如下:
其中Yes / No是Classifier1正确且Classifier2不正确的检验实例的计数,No / Yes是Classifier1不正确且Classifier2正确的检验实例的计数。
检验统计量的这种计算假定计算中使用的列联表中的每个单元具有至少25个计数。检验统计量具有1自由度的卡方分布。
我们可以看到,只使用列联表的两个元素,即Yes/Yes和No/No元素没有用于检验统计数据的计算。因此,我们可以看到统计数据是报告两个模型之间的正确或错误的预测,而不是准确性或错误率。当对统计数据的发现提出要求时,这一点非常重要。
检验的默认假设或零假设是两个案例不同一致的总计。如果零假设被拒绝,有证据表明,这些案例在不同的方面存在分歧,这些分歧是有倾向性的。
给定显着性水平的选择,通过检验计算的p值可以解释如下:
花点时间去理解,如何在两个机器学习分类器模型的上下文中解释检验结果是很重要的。
计算McNemar检验时使用的两个项去捕捉了两个模型的误差。具体而言,列联表中的No / Yes和Yes / No。该检验检查它们两个计数之间是否存在显著的差异。
如果它们具有相似的计数,则表明两个模型犯错误的比例大致相同,仅在测试集的不同实例上。在这种情况下,零假设也不会被拒绝。
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
反之,技术如果不相似,则表明两个模型不仅产生不同的错误,而且实际上在测试集上相对的错误比例也不同。在这种情况下,我们将拒绝零假设。
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
我们可以总结如下:
在执行检测并找到显著的结果之后,报告效果统计测量以量化该发现可能是有用的。例如,一个自然的选择是报告优势比,或列联表本身,尽管这两者都假设一个“sophisticated reader”。
报告在测试集上两个分类器之间的差异可能很有用。在这种情况下,请小心你的声明,因为显著性的检验不会报告模型之间的错误差异,只会报告模型之间错误比例的相对偏差。
最后,在使用McNemar检验中,Dietterich强调了必须考虑的两个重要限制。他们是:
通常,模型行为基于用来拟合模型的特定训练数据而变化。
这是由于模型与特定训练实例的交互作用以及在学习过程中使用的随机性。将模型拟合到多个不同的训练数据集并评估技能(如重采样方法所做的那样),提供了一种度量模型差异的方法。
如果可变性的来源很小,则该检验是合适的。
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
两个分类器在一个测试集上进行评估,并且测试集应该小于训练集。
这与更多的是使用重采样方法的假设检验不同,因为在评估期间,数据集可用作测试集。
这提供了较少的机会来比较模型的性能。它要求测试集适当地代表域,这通常意味着测试数据集很大。
在Python中可以使用mcnemar()Statsmodels函数实现McNemar检验。
该函数将列联表作为参数,并返回计算出的检验统计量和p值。
根据数据量,有两种方法可以使用统计信息。如果表中有一个单元用于计算计数小于25的测试统计量,则使用检验的修改版本,使用二项分布计算精确的p值。这是该检验的默认用法:
或者,如果在列联表中计算检验统计量时使用的所有单元具有25或更大的值,则可以使用检验的标准计算:
我们可以在上面描述的示例列联表上计算McNemar检验。这个列联表在两个不同的单元中都有一个小的计数,因此必须使用精确的方法。
完整的示例如下:
运行该示例计算列联表上的统计值和p值并打印结果。
我们可以看到,该检验强有力地证实了两种案例之间的分歧差别很小。零假设没有被拒绝。当我们使用检验来比较分类器时,我们声明两种模型之间的分歧没有统计学上的显著差异。
如果希望深入了解,本节提供更多相关资源。
在本教程中,你了解了如何使用McNemar统计假设检验来比较单个测试数据集上的机器学习分类模型。
具体来说,你学到了:
在1998年被广泛引用的论文中,Thomas Dietterich在训练多份分类器模型副本昂贵而且不切实际的情况下推荐了McNemar检验。
它描述了深度学习模型的现状,模型非常大并且在大型数据集上进行训练和评估,一个模型通常需要数天或数周来训练。
在本教程中,你将了解如何使用McNemar统计假设检验来比较单个测试数据集上的机器学习分类模型。
完成本教程后,你将了解:
- McNemar检验适合大型深度学习模型。
- 如何将两个分类器的预测结果转换为列联表,以及如何使用它来计算McNemar检验中的统计量。
- 如何用Python计算McNemar检验并解释和报告结果。
让我们开始吧。

教程概述
本教程分为五个部分; 他们是:
- 为深度学习执行统计假设检验
- 列联表
- McNemar检验的统计
- 使用McNemar检验解释分类器
- Python中的McNemar检验
为深度学习执行统计假设检验
Thomas Dietterich在他1998年发表的一篇重要的、被广泛引用的论文中,讨论了如何利用统计假设检验来比较分类器,论文“Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms”。链接:https://www.mitpressjournals.org/doi/abs/10.1162/089976698300017197
具体来说,当被比较的算法只能进行一次评估时推荐使用该检验,例如在一个测试集上,而不是通过重采样技术反复评估,例如k折交叉验证。
对于只能执行一次的算法,McNemar检验是唯一具有可接受的第一类(Type I )错误的检验。
-Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
具体来说,Dietterich的研究涉及不同统计假设检验的评估,其中一些检验使用了重采样方法的结果。研究的关注点是低的第一类错误,即统计检验报告了为有影响实际上没有(假阳性)。
统计检验可以比较基于单一测试集的模型,这对现代机器学习来说十分重要,特别是在深度学习领域。
深度学习模型通常本身就很大,并且在非常大的数据集上运行。总之,这些因素可能意味着在现代硬件上对模型的训练可能需要数天甚至数周时间。
这排除了用重新采样方法比较模型的实际应用,并暗示了需要使用可以在单个测试数据集上评估训练模型结果的检验。
McNemar检验适合评估这些大型的、训练慢的深度学习模型。
列联表
McNemar检验基于列联表运行。在我们深入了解这种检验之前,让我们花点时间来理解如何计算两个分类器的列联表。
列联表是两个分类变量的制表或者说计数。在McNemar检验的情况下,我们对二元变量的正确/不正确(或者是/否)的控制和处理感兴趣(或者两种都有)。这被称为2×2列联表。
列联表乍一看可能并不直观。让我们做一个具体的例子。
我们有两个训练好的分类器。每个分类器对测试数据集中的10个实例中的每个实例进行二元分类预测。预测被评估并确定为正确的或不正确的(yes/no)。
然后我们可以在表格中汇总这些结果,如下所示:

我们可以看到Classifier1得到6个Yes,或者说准确率为60%,Classifier2得到5个Yes,或者在测试集上有50%的准确率。
该表现在可以简化为列联表。
列联表依赖于这样一个事实 — 两个分类器都在完全相同的训练数据上训练并在完全相同的测试数据上进行评估。
列联表具有以下结构:
Classifier2 Correct, Classifier2 Incorrect
Classifier1 Correct ?? ??
Classifier1 Incorrect ?? ??
对于表中第一个单元格的情况,我们必须总结Classifier1得到正确且Classifier2也得到正确的检验实例的总数。例如,两个分类器正确预测的第一个实例是实例5.两个分类器正确预测的实例总数为4。
考虑到这点,另一种更具编程性的方法是在上面的结果表中对“是/否”的每个组合求和。
Classifier2 Correct, Classifier2 Incorrect
Classifier1 Correct Yes/Yes Yes/No
Classifier1 Incorrect No/Yes No/No
结果如下:
Classifier2 Correct, Classifier2 Incorrect
Classifier1 Correct 4 2
Classifier1 Incorrect 1 3
McNemar检验的统计
McNemar检验是配对的非参数或无分布统计假设检验。
它也不像其他一些统计假设检验那么直观。
McNemar检验是检查两个案例之间的分歧是否匹配。从技术上讲,这被称为列联表的同质性(homogeneity ,特别是边际同质性)。因此,McNema检验是一种列联表的同质性检验。
这个检验广泛用于医学领域,可以比较治疗对照的效果。
在比较两个二元分类算法时,检验是这两个模型是否存在相同的分歧的说明。它不会说明一个模型是否比另一个模型更准确或更容易出错。当我们看统计数据是如何计算的时候,这一点是显而易见的。
McNemar检验统计量的计算如下:
statistic = (Yes/No - No/Yes)^2 / (Yes/No + No/Yes)
其中Yes / No是Classifier1正确且Classifier2不正确的检验实例的计数,No / Yes是Classifier1不正确且Classifier2正确的检验实例的计数。
检验统计量的这种计算假定计算中使用的列联表中的每个单元具有至少25个计数。检验统计量具有1自由度的卡方分布。
我们可以看到,只使用列联表的两个元素,即Yes/Yes和No/No元素没有用于检验统计数据的计算。因此,我们可以看到统计数据是报告两个模型之间的正确或错误的预测,而不是准确性或错误率。当对统计数据的发现提出要求时,这一点非常重要。
检验的默认假设或零假设是两个案例不同一致的总计。如果零假设被拒绝,有证据表明,这些案例在不同的方面存在分歧,这些分歧是有倾向性的。
给定显着性水平的选择,通过检验计算的p值可以解释如下:
- p> alpha:未能拒绝H0,在分歧上没有差异(例如,治疗没有效果)。
- p <= alpha:拒绝H0,分歧的显着差异(例如,治疗有效)。
使用McNemar检验解释分类器
花点时间去理解,如何在两个机器学习分类器模型的上下文中解释检验结果是很重要的。
计算McNemar检验时使用的两个项去捕捉了两个模型的误差。具体而言,列联表中的No / Yes和Yes / No。该检验检查它们两个计数之间是否存在显著的差异。
如果它们具有相似的计数,则表明两个模型犯错误的比例大致相同,仅在测试集的不同实例上。在这种情况下,零假设也不会被拒绝。
在零假设下,两种算法应该具有相同的错误率......
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
反之,技术如果不相似,则表明两个模型不仅产生不同的错误,而且实际上在测试集上相对的错误比例也不同。在这种情况下,我们将拒绝零假设。
因此,我们可以拒绝零假设,支持两种算法在特定训练中训练时具有不同性能的假设
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
我们可以总结如下:
- 不拒绝零假设:分类器在测试集上具有相似的错误比例。
- 拒绝零假设:分类器在测试集上具有不同的错误比例。
在执行检测并找到显著的结果之后,报告效果统计测量以量化该发现可能是有用的。例如,一个自然的选择是报告优势比,或列联表本身,尽管这两者都假设一个“sophisticated reader”。
报告在测试集上两个分类器之间的差异可能很有用。在这种情况下,请小心你的声明,因为显著性的检验不会报告模型之间的错误差异,只会报告模型之间错误比例的相对偏差。
最后,在使用McNemar检验中,Dietterich强调了必须考虑的两个重要限制。他们是:
1.没有训练集或模型可变性的度量。
通常,模型行为基于用来拟合模型的特定训练数据而变化。
这是由于模型与特定训练实例的交互作用以及在学习过程中使用的随机性。将模型拟合到多个不同的训练数据集并评估技能(如重采样方法所做的那样),提供了一种度量模型差异的方法。
如果可变性的来源很小,则该检验是合适的。
因此,只有当我们认为这些可变性来源很小时,才应该应用McNemar检验。
- Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithm,1998。
2.较少的模型直接比较
两个分类器在一个测试集上进行评估,并且测试集应该小于训练集。
这与更多的是使用重采样方法的假设检验不同,因为在评估期间,数据集可用作测试集。
这提供了较少的机会来比较模型的性能。它要求测试集适当地代表域,这通常意味着测试数据集很大。
Python中的McNemar检验
在Python中可以使用mcnemar()Statsmodels函数实现McNemar检验。
该函数将列联表作为参数,并返回计算出的检验统计量和p值。
根据数据量,有两种方法可以使用统计信息。如果表中有一个单元用于计算计数小于25的测试统计量,则使用检验的修改版本,使用二项分布计算精确的p值。这是该检验的默认用法:
stat, p = mcnemar(table, exact=True)
或者,如果在列联表中计算检验统计量时使用的所有单元具有25或更大的值,则可以使用检验的标准计算:
stat, p = mcnemar(table, exact=False, correction=True)
我们可以在上面描述的示例列联表上计算McNemar检验。这个列联表在两个不同的单元中都有一个小的计数,因此必须使用精确的方法。
完整的示例如下:
# Example of calculating the mcnemar test
from statsmodels.stats.contingency_tables import mcnemar
# define contingency table
table = [[4, 2],
[1, 3]]
# calculate mcnemar test
result = mcnemar(table, exact=True)
# summarize the finding
print('statistic=%.3f, p-value=%.3f' % (result.statistic, result.pvalue))
# interpret the p-value
alpha = 0.05
if result.pvalue > alpha:
print('Same proportions of errors (fail to reject H0)')
else:
print('Different proportions of errors (reject H0)')
运行该示例计算列联表上的统计值和p值并打印结果。
我们可以看到,该检验强有力地证实了两种案例之间的分歧差别很小。零假设没有被拒绝。当我们使用检验来比较分类器时,我们声明两种模型之间的分歧没有统计学上的显著差异。
statistic=1.000, p-value=1.000
Same proportions of errors (fail to reject H0)
扩展阅读
如果希望深入了解,本节提供更多相关资源。
论文
- https://link.springer.com/article/10.1007/BF02295996
- https://www.mitpressjournals.org/doi/abs/10.1162/089976698300017197
API
- statsmodels.stats.contingency_tables.mcnemar()API(http://www.statsmodels.org/dev/generated/statsmodels.stats.contingency_tables.mcnemar.html)
总结
在本教程中,你了解了如何使用McNemar统计假设检验来比较单个测试数据集上的机器学习分类模型。
具体来说,你学到了:
- McNemar检验适合大型深度学习模型。
- 如何将两个分类器的预测结果转换为列联表,以及如何使用它来计算McNemar检验中的统计量。
- 如何用Python计算McNemar检验并解释和报告结果。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























