SigOpt数据的近似——从不完整数据进行预测的技术。
2017年11月06日 由 荟荟 发表
139238
0
在之前关于SigOpt Fundamentals的文章中,我们介绍了高斯过程 和 协方差内核的概念 。使用这些及其它工具,SigOpt帮助企业有效地优化其关键指标,包括 收入在A / B测试, 精度机器学习模型,和 复杂的模拟输出。为了解决可能包含许多变量/参数的问题,我们建议公司进行一系列实验。这些实验创建的数据具有与公司参数一样多的维度,我们SigOpt的目标之一是使用此观察数据预测未观察到的值,以确定这些关键指标的最佳值。我们将此过程称为获取数据并使预测 近似。
近似的需要可能不会立即显而易见; 如果你在驾驶并且你需要知道你的速度,你可能只是检查速度表,而不是根据你往下看的最后五次来近似。实际上,在一个完美的世界中,每个人都可以进行任意多次的实验,从而可以轻松地在任何所需位置生成数据,并且无需进行近似或优化。不幸的是,最常感兴趣的实验是昂贵的,需要大量的时间和/或资源。SigOpt试图通过从有限数量的实验中提取尽可能多的信息来最小化这种支出。下图左侧有一个图表,显示了观测数据和可用于预测的数据的三种可能近似值。
[caption id="attachment_29303" align="aligncenter" width="540"]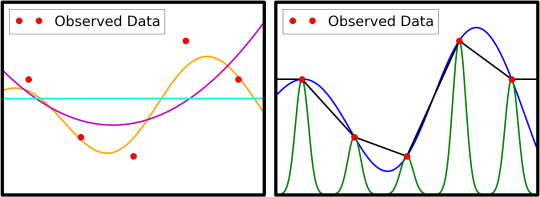 图 1: 5周的观察显示为红色,与各种预测曲线沿。左边的图表显示了观察数据的三个近似值。在右边,我们看到一个图表有三个不同的近似值,所有这些都是插值(通过观察到的红色圆圈)。[/caption]
图 1: 5周的观察显示为红色,与各种预测曲线沿。左边的图表显示了观察数据的三个近似值。在右边,我们看到一个图表有三个不同的近似值,所有这些都是插值(通过观察到的红色圆圈)。[/caption]
当SigOpt想要创建近似值时,我们首先转向 高斯过程 ; 它们只是更大计划的一部分,但可能是最重要的部分。高斯过程的近似是重要的,因为来自高斯过程的预测 对数据执行 插值。 如果预测完全重现所有观察结果,我们说过程会 插入观察到的数据。右上图显示了对给定数据进行插值的预测示例 - 将右侧的插值与左侧的近似值进行对比,而不是插值数据。 Fidelity 是我们用来描述精确预测如何匹配观察的术语:插值具有完美的保真度。
如上图所示,没有可用于根据给定数据进行预测的唯一近似值; 事实上,即使我们要求完美的保真度,也有无数[1]多条预测曲线。那么,我们如何决定应该使用哪些来进行预测呢?为此,我们使用一种称为正则化 [2] 的机制 ,它为我们提供了一个标准,通过该标准我们可以区分具有相同保真度的不同插值。对于此设置,预测曲线的规律性定义为“平静”; 在下图中,我们描述了具有各种规律性的预测。一般而言,优选具有高规律性的曲线,因为预测表现得更好并且不太容易出现不稳定的行为。
[caption id="attachment_29304" align="aligncenter" width="540"]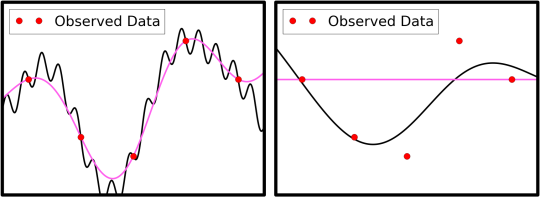 图 2: 在左边是两个插值和右边两个近似我们前面看到的相同的数据。在两张图片中,粉红色曲线比黑色曲线具有更大的规律性。[/caption]
图 2: 在左边是两个插值和右边两个近似我们前面看到的相同的数据。在两张图片中,粉红色曲线比黑色曲线具有更大的规律性。[/caption]
那么,让我们重温一下我们所处的位置:
我们可以对观察到的数据产生无限多的插值预测。每个都具有完美的保真度。我们可以(某种方式)测量预测曲线的规律性。我们更喜欢高规律性曲线以防止不稳定的预测。高保真度(预测紧密跟随数据)和高规律性(预测不是不稳定)是无关的。
根据我们迄今为止所看到的,有效预测的一种策略是创建具有高规律性的插值。幸运的是,高斯过程(内插观测数据)自动最大化了规律性的关键测量[3],使它们成为这项工作的一个很好的工具。不幸的是,高斯过程预测并不适用于所有情况。我们将在下面看到,完美的保真度并不总是令人满意的,需要通过插值进行修改以做出可行的预测。
SigOpt修改我们的高斯过程预测的一个重要原因是因为SigOpt客户经常在存在不确定性的情况下进行观察 。我们将此类观察称为噪声[4]数据,其中任何观测值都有一些 差异 且无法完全信任。下图介绍了测量可以伴随方差估计的想法,该方法描述了观测值仅是该位置可能值的指导。
[caption id="attachment_29305" align="aligncenter" width="540"]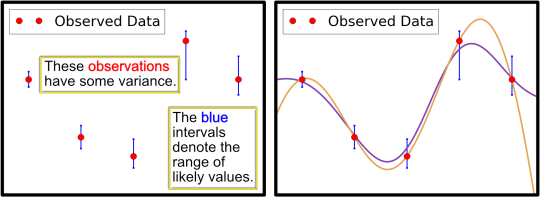 图 3: 在这里,我们像以前一样考虑同样的意见,但现在这些意见有一定的不确定性。蓝色条应由观察者决定。由于观察数据的变化,可能不清楚更高保真度(橙色)或更高规则性(紫色)近似是否是优选的。[/caption]
图 3: 在这里,我们像以前一样考虑同样的意见,但现在这些意见有一定的不确定性。蓝色条应由观察者决定。由于观察数据的变化,可能不清楚更高保真度(橙色)或更高规则性(紫色)近似是否是优选的。[/caption]
在处理噪声数据时(几乎所有人都是这样),预测的保真度可能是一个棘手的问题。一方面,我们希望尊重观察到的结果,如果没有其他原因,因为它们获得的成本很高,如果结果未被使用,很难证明昂贵的实验是合理的。另一方面,对于具有不确定性的观察,我们应该想要预测该位置的最可能值,而不仅仅是我们碰巧观察到的值。下面我们看到一个描绘这个难题的数字; 特别是,由于包含更多噪声数据,插值预测可能具有不合理的振荡。在我们寻找最佳参数时,这些振荡可能会产生误导并导致不必要的实验,从而耗费客户的时间和资源。
[caption id="attachment_29306" align="aligncenter" width="540"]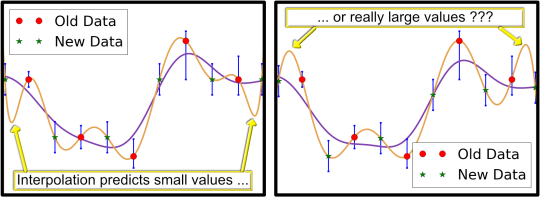 图 4: 随着越来越多的噪声数据观察(新绿点),我们看到更高的规律性的真正价值。比较左右图像,注意新值的微小差异会产生明显不同的橙色插值。相比之下,高规律性的紫色预测具有较低的保真度,但受这些小差异的影响要小得多。[/caption]
图 4: 随着越来越多的噪声数据观察(新绿点),我们看到更高的规律性的真正价值。比较左右图像,注意新值的微小差异会产生明显不同的橙色插值。相比之下,高规律性的紫色预测具有较低的保真度,但受这些小差异的影响要小得多。[/caption]
任何从嘈杂数据中预测未观察到的结果的尝试都需要在保真度和规律性之间取得平衡:在相信你的眼睛和认识到它们可能对你撒谎之间取得平衡[5]。适当地选择这种平衡本身就是一个有趣的问题,可以用例如交叉验证来解决 。SigOpt为客户提供了根据他们的观察定义不确定性的机会,并且利用这些知识,我们可以平衡观察到的结果与他们的方差,以进行预测并确定不确定性背后的真实行为。通过适当的权衡,我们可以指导您以更少的试验和错误获得更好的结果。 立即注册 免费试用版,以帮助您消除噪音并获得更好的结果。
[1]:能够保证的插值涉及 财产 的 unisolvency,这是重要的,但超出了本文的范围。
[2]: 正则化 是数学中广泛使用的术语。从最普遍的意义上讲,对于不存在唯一解决方案的问题,需要一个问题的正则化形式。但要完全理解这一点,我们需要讨论存在和唯一性的重要主题,这需要他们自己的博客文章。对于这篇文章,将正则化视为将插值问题重新描述为更一般的近似框架就足够了,该框架平衡了保真度和规律性。
[3]:这种测量通常涉及一种 规范,这也很重要,但超出了本文的范围。我称之为“关键测量”的标准是 再生核Hilbert空间 范数。
[4]:我偶然发现了噪声数据的定义,这些数据将其等同于 无意义的数据,我发现这种比较极具误导性。可以说,损坏的数据毫无意义:考虑一个人身高的测量值,这些测量值被他们的脚趾数量意外地取代,作为腐败和无意义数据的一个例子。但是大多数观察都有一定程度的差异/噪音(谢谢 Heisenberg),这并没有阻止我们使用数据来制造汽车,手机和电脑。当你想到嘈杂的数据时,我希望你不要认为它没有意义; 它只是存在不确定性的数据。
[5]:设计这种平衡策略对于找到适合它的近似值更为重要。我最近的书中的第15章和第18章 提供了关于具有清晰定义的预测的共同策略的一些讨论和引用。
近似的需要可能不会立即显而易见; 如果你在驾驶并且你需要知道你的速度,你可能只是检查速度表,而不是根据你往下看的最后五次来近似。实际上,在一个完美的世界中,每个人都可以进行任意多次的实验,从而可以轻松地在任何所需位置生成数据,并且无需进行近似或优化。不幸的是,最常感兴趣的实验是昂贵的,需要大量的时间和/或资源。SigOpt试图通过从有限数量的实验中提取尽可能多的信息来最小化这种支出。下图左侧有一个图表,显示了观测数据和可用于预测的数据的三种可能近似值。
[caption id="attachment_29303" align="aligncenter" width="540"]
 图 1: 5周的观察显示为红色,与各种预测曲线沿。左边的图表显示了观察数据的三个近似值。在右边,我们看到一个图表有三个不同的近似值,所有这些都是插值(通过观察到的红色圆圈)。[/caption]
图 1: 5周的观察显示为红色,与各种预测曲线沿。左边的图表显示了观察数据的三个近似值。在右边,我们看到一个图表有三个不同的近似值,所有这些都是插值(通过观察到的红色圆圈)。[/caption]当SigOpt想要创建近似值时,我们首先转向 高斯过程 ; 它们只是更大计划的一部分,但可能是最重要的部分。高斯过程的近似是重要的,因为来自高斯过程的预测 对数据执行 插值。 如果预测完全重现所有观察结果,我们说过程会 插入观察到的数据。右上图显示了对给定数据进行插值的预测示例 - 将右侧的插值与左侧的近似值进行对比,而不是插值数据。 Fidelity 是我们用来描述精确预测如何匹配观察的术语:插值具有完美的保真度。
如上图所示,没有可用于根据给定数据进行预测的唯一近似值; 事实上,即使我们要求完美的保真度,也有无数[1]多条预测曲线。那么,我们如何决定应该使用哪些来进行预测呢?为此,我们使用一种称为正则化 [2] 的机制 ,它为我们提供了一个标准,通过该标准我们可以区分具有相同保真度的不同插值。对于此设置,预测曲线的规律性定义为“平静”; 在下图中,我们描述了具有各种规律性的预测。一般而言,优选具有高规律性的曲线,因为预测表现得更好并且不太容易出现不稳定的行为。
[caption id="attachment_29304" align="aligncenter" width="540"]
 图 2: 在左边是两个插值和右边两个近似我们前面看到的相同的数据。在两张图片中,粉红色曲线比黑色曲线具有更大的规律性。[/caption]
图 2: 在左边是两个插值和右边两个近似我们前面看到的相同的数据。在两张图片中,粉红色曲线比黑色曲线具有更大的规律性。[/caption]那么,让我们重温一下我们所处的位置:
我们可以对观察到的数据产生无限多的插值预测。每个都具有完美的保真度。我们可以(某种方式)测量预测曲线的规律性。我们更喜欢高规律性曲线以防止不稳定的预测。高保真度(预测紧密跟随数据)和高规律性(预测不是不稳定)是无关的。
根据我们迄今为止所看到的,有效预测的一种策略是创建具有高规律性的插值。幸运的是,高斯过程(内插观测数据)自动最大化了规律性的关键测量[3],使它们成为这项工作的一个很好的工具。不幸的是,高斯过程预测并不适用于所有情况。我们将在下面看到,完美的保真度并不总是令人满意的,需要通过插值进行修改以做出可行的预测。
SigOpt修改我们的高斯过程预测的一个重要原因是因为SigOpt客户经常在存在不确定性的情况下进行观察 。我们将此类观察称为噪声[4]数据,其中任何观测值都有一些 差异 且无法完全信任。下图介绍了测量可以伴随方差估计的想法,该方法描述了观测值仅是该位置可能值的指导。
[caption id="attachment_29305" align="aligncenter" width="540"]
 图 3: 在这里,我们像以前一样考虑同样的意见,但现在这些意见有一定的不确定性。蓝色条应由观察者决定。由于观察数据的变化,可能不清楚更高保真度(橙色)或更高规则性(紫色)近似是否是优选的。[/caption]
图 3: 在这里,我们像以前一样考虑同样的意见,但现在这些意见有一定的不确定性。蓝色条应由观察者决定。由于观察数据的变化,可能不清楚更高保真度(橙色)或更高规则性(紫色)近似是否是优选的。[/caption]在处理噪声数据时(几乎所有人都是这样),预测的保真度可能是一个棘手的问题。一方面,我们希望尊重观察到的结果,如果没有其他原因,因为它们获得的成本很高,如果结果未被使用,很难证明昂贵的实验是合理的。另一方面,对于具有不确定性的观察,我们应该想要预测该位置的最可能值,而不仅仅是我们碰巧观察到的值。下面我们看到一个描绘这个难题的数字; 特别是,由于包含更多噪声数据,插值预测可能具有不合理的振荡。在我们寻找最佳参数时,这些振荡可能会产生误导并导致不必要的实验,从而耗费客户的时间和资源。
[caption id="attachment_29306" align="aligncenter" width="540"]
 图 4: 随着越来越多的噪声数据观察(新绿点),我们看到更高的规律性的真正价值。比较左右图像,注意新值的微小差异会产生明显不同的橙色插值。相比之下,高规律性的紫色预测具有较低的保真度,但受这些小差异的影响要小得多。[/caption]
图 4: 随着越来越多的噪声数据观察(新绿点),我们看到更高的规律性的真正价值。比较左右图像,注意新值的微小差异会产生明显不同的橙色插值。相比之下,高规律性的紫色预测具有较低的保真度,但受这些小差异的影响要小得多。[/caption]任何从嘈杂数据中预测未观察到的结果的尝试都需要在保真度和规律性之间取得平衡:在相信你的眼睛和认识到它们可能对你撒谎之间取得平衡[5]。适当地选择这种平衡本身就是一个有趣的问题,可以用例如交叉验证来解决 。SigOpt为客户提供了根据他们的观察定义不确定性的机会,并且利用这些知识,我们可以平衡观察到的结果与他们的方差,以进行预测并确定不确定性背后的真实行为。通过适当的权衡,我们可以指导您以更少的试验和错误获得更好的结果。 立即注册 免费试用版,以帮助您消除噪音并获得更好的结果。
[1]:能够保证的插值涉及 财产 的 unisolvency,这是重要的,但超出了本文的范围。
[2]: 正则化 是数学中广泛使用的术语。从最普遍的意义上讲,对于不存在唯一解决方案的问题,需要一个问题的正则化形式。但要完全理解这一点,我们需要讨论存在和唯一性的重要主题,这需要他们自己的博客文章。对于这篇文章,将正则化视为将插值问题重新描述为更一般的近似框架就足够了,该框架平衡了保真度和规律性。
[3]:这种测量通常涉及一种 规范,这也很重要,但超出了本文的范围。我称之为“关键测量”的标准是 再生核Hilbert空间 范数。
[4]:我偶然发现了噪声数据的定义,这些数据将其等同于 无意义的数据,我发现这种比较极具误导性。可以说,损坏的数据毫无意义:考虑一个人身高的测量值,这些测量值被他们的脚趾数量意外地取代,作为腐败和无意义数据的一个例子。但是大多数观察都有一定程度的差异/噪音(谢谢 Heisenberg),这并没有阻止我们使用数据来制造汽车,手机和电脑。当你想到嘈杂的数据时,我希望你不要认为它没有意义; 它只是存在不确定性的数据。
[5]:设计这种平衡策略对于找到适合它的近似值更为重要。我最近的书中的第15章和第18章 提供了关于具有清晰定义的预测的共同策略的一些讨论和引用。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























