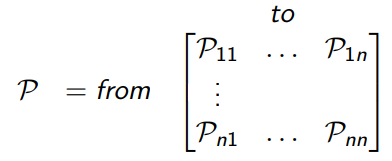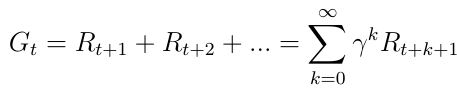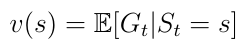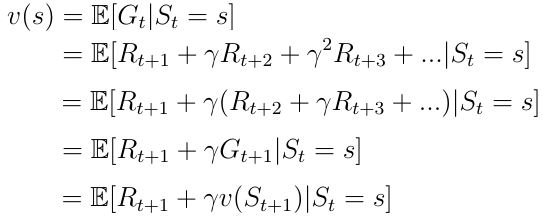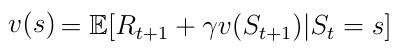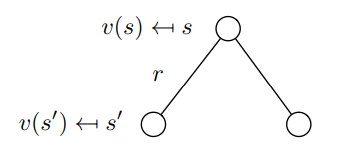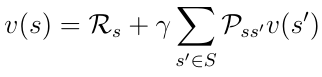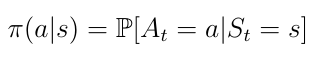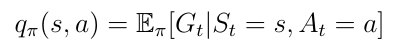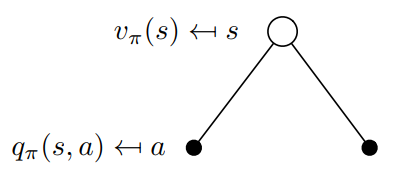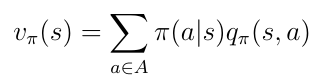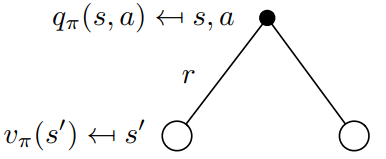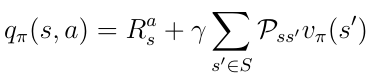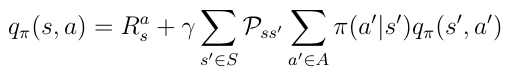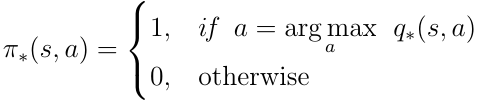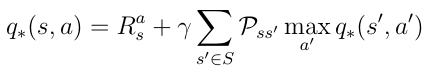这是关于自学习AI智能体系列的第一篇文章，或者我们可以更准确地称之为 - 深度强化学习。本系列文章的目的不仅仅是让你对这些概念有一个直观的认识。而是想让你更深入地理解深度强化学习最流行也最有效的方法背后的理论，数学原理和实现。

自学习AI智能体系列目录：

• 第一部分：马尔可夫决策过程（本文）


• 第二部分：Deep Q-Learning(DQN)


• 第三部分：Deep (Double) Q-Learning


• 第四部分：连续动作空间的梯度策略（Policy Gradients for Continues Action Spaces）


• 第五部分：决斗网络（Dueling Networks）


• 第六部分：异步评价智能体（Asynchronous Actor-Critic Agents）

AI学会了如何奔跑和越障

目录

• 0.简介


• 1.强化学习简述


• 2.马尔可夫决策过程


• 2.1马尔可夫过程


• 2.2马尔可夫奖励过程


• 2.3价值函数


• 3.贝尔曼方程（Bellman Equation）


• 3.1马尔可夫奖励过程的贝尔曼方程


• 3.2马尔可夫决策过程 -  定义


• 3.3策略


• 3.4动作价值函数


• 3.5最优策略


• 3.6 贝尔曼最优方程

0.简介

近些年来，深度强化学习正在兴起。世界各地的研究人员和大众媒体对其的关注超过了深度学习的其他子领域。在深度学习方面取得的最大成就是源自深度强化学习。从来自谷歌的Alpha Go在围棋游戏中击败了世界上最强的人类玩家（(这一成就在几年前被认为是不可能实现的）到DeepMind的 AI智能体自学走路，跑步和越障 。

AI智能体学会了如何跑步和越障。

AI智能体学会了如何跑步和越障。

自2014年以来，其他人工智能智能体在老式雅达利（Atari）游戏比如下面的打砖块（Breakthrough）中超过了人类水平。在我看来，这一切的最令人惊奇的是，这些AI智能体中不是由人类明确编程或教导如何解决这些任务。他们通过深度学习和强化学习的力量自学的。这一篇文章的目标是为你提供必要的数学基础，以便为下文打下基础。

AI智能体学习了如何玩打砖块

1.强化学习简述

所谓深度强化学习，说白了是构建一个直接从与环境的交互中学习的算法（即AI智能体）（图5）。环境可以是现实世界、计算机游戏，模拟系统甚至是棋盘游戏，如围棋或国际象棋。与人类一样，AI智能体从其行为的结果中学习（而不是直接教）。

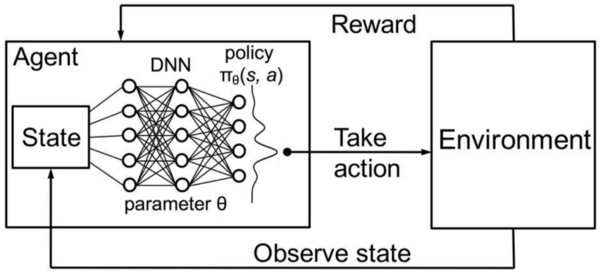
深度强化学习的示意图

在深度强化学习中，智能体由神经网络代表。神经网络直接与环境交互。它指出当前环境的状态，并根据当前状态和过去的经验决定采取何种动作(例如向左、向右移动等)。基于所采取的动作，AI智能体得到奖励。奖励的大小决定解决给定问题所采取动作的质量。智能体的目标是学习在任何特定情况下要采取的动作，并随着时间的推移最大化累积奖励。

2.马尔可夫决策过程

马尔可夫决策过程（MDP）是一个离散时间随机控制过程。MDP是迄今为止为AI智能体的复杂环境建模的最佳方法。智能体需要解决的每个问题可以被认为是状态序列S1，S2，S3，... Sn（状态可以是围棋或象棋棋盘的布局）。智能体执行操作并从一个状态移动到另一个状态。接下来，你将学习确定智能体在给定情况下必须采取何种动作的数学原理。

2.1马尔可夫过程

马尔可夫过程是描述可能状态序列的随机模型，其中，当前状态仅依赖于先前的状态。这也称为马尔可夫特性（Markov Property）（Eq.1）。对于强化学习，这意味着AI智能体的下一个状态仅取决于最后一个状态而不是之前的所有先前状态。

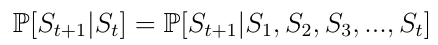
Eq.1马尔可夫特性

马尔可夫过程是一个随机过程。这意味着从当前状态s到下一个状态s'的转换只能以某个概率Pss '（等式2）发生。在马尔可夫过程中，智能体只能以特定的向左移动的概率被告知向左走（例如0.998）。由环境决定智能体最终结果的可能性很小。

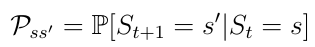
Eq.2从状态s到状态 s'的转换概率

Pss '可以被认为是状态转移矩阵P中的条目（entry），它定义从所有状态 s到所有后续状态 s'的转移概率（等式3）。

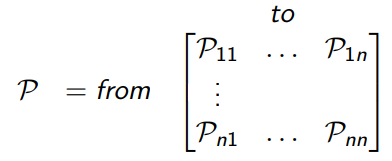
Eq.3转移概率矩阵

注意：马尔可夫过程（或者说，马尔可夫链）是一个元组< S，P > 。S是一组（有限的）状态。P是状态转移概率矩阵。

2.2马尔可夫奖励过程

马尔可夫奖励过程是元组< S，P，R >。这里R是智能体希望在状态s中获得的奖励（等式4）。该过程基于这样一个事实：对于旨在实现某个目标（例如赢得国际象棋游戏）的AI智能体，某些状态（游戏配置）在策略和赢得游戏的潜在可能比其他状态更大。

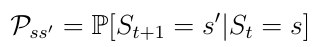
Eq.4状态s的预期奖励

我们主要关心总奖励Gt（等式5），它是智能体在所有状态的序列中获得的预期累积奖励。每个奖励都由折扣系数（discount factor）γ∈[0,1]加权。由于它没有循环马尔可夫过程中的无限奖励，折扣奖励的数学方法很简单。除了折扣系数意味着我们未来越多，奖励就越不重要，因为未来往往是不确定的。如果奖励是金融奖励，即时奖励可能比延迟奖励获得更多利息。动物或人类的行为也表现出表现出对即时奖励的偏好。

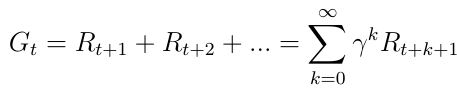
Eq.5所有状态的总奖励

2.3价值函数

另一个重要的概念是价值函数v（s）。价值函数将价值映射到每个状态s。状态s的价值被定义为AI智能体在状态s中开始行动将获得的预期总奖励（等式6）。

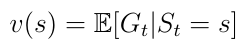
Eq.6价值函数，从状态s开始的预期收益

价值函数可以分解为两部分：

• 智能体接收的直接奖励R（t + 1）处于状态s。


• 状态s之后的下一状态的折扣系数v（s（t + 1））。

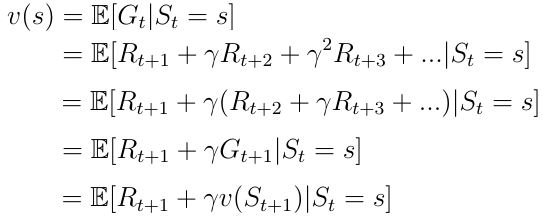
Eq.7分解价值函数

3.贝尔曼方程

3.1 马尔可夫奖励过程的贝尔曼方程

分解的价值函数（公式8）也称为马尔可夫奖励过程的贝尔曼方程。该函数可以在节点图中显示（如下）。从状态s开始得到价值v（s）。处于状态s我们有一定的概率Pss'到下一个状态s'。在这种情况下，我们有两个可能的下一状态。 为了获得值v（s），我们必须计算由概率Pss'加权的可能的下一个状态价值v（s'）的总数并加上加上状态s的即时奖励 。这就是公式9，只不过是在方程中执行了期望算子的公式8。

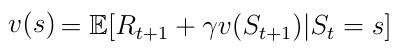
Eq.8分解值函数

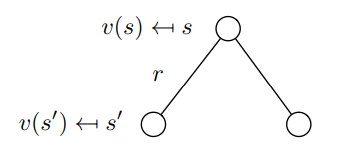
从s到 s'的随机过渡

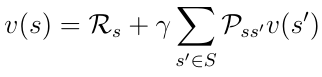
Eq.9执行期望算子E后的贝尔曼方程

3.2马尔可夫决策过程 - 定义

马尔可夫决策过程是马尔可夫奖励过程的决策。马尔可夫决策过程由一组元组描述，其中A是智能体可以在状态s中采取的可能动作的有限集合。因此，处于状态s的即时奖励现在也取决于智能体在这种状态下采取的行动a (公式10)。

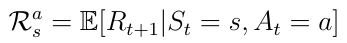
Eq.10预期奖励取决于状态内的动作

3.3策略

在这里，我们将讨论智能体如何确定在特定状态下必须采取哪些动作。这由所谓的策略π（公式11）决定。从数学角度讲，策略是对给定状态的所有动作的分配。策略决定了从状态s到智能体必须采取的操作a的映射。

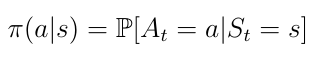
Eq.11从s到a的映射的策略

直观地说策略π可以被描述为一个智能体根据当前状态s选择某些动作的一种对策。

策略使状态价值函数v（s）重新定义（公式12），我们现在将其定义为从状态s开始然后遵循策略π的的预期回报。

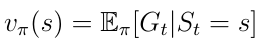
Eq.12状态价值函数

3.4动作价值函数

除状态值函数之外，另一个重要函数是动作价值函数q（s，a）（等式13）。动作价值函数是我们从状态s开始采取动作a然后遵循策略π获得的预期回报。值得注意得失，对于状态s，q（s，a）可以采用多个值，因为智能体可以在状态s中执行多个动作。Q（s，a）的计算是通过神经网络实现的。给定一个状态s作为输入，网络计算该状态下每个可能动作的质量(Quality)作为标量（如下图）。更高的质量意味着对给定目标采取更好的动作。

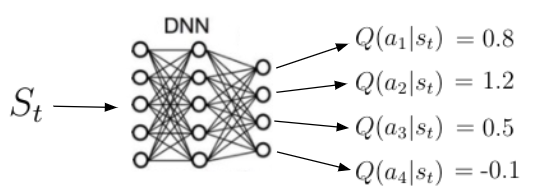
动作价值函数的图示

动作价值函数告诉我们在特定状态下采取特定动作有多好。

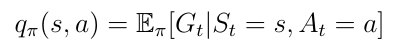
Eq.13动作价值函数

先前的状态值函数v（s）可以分解为以下形式：

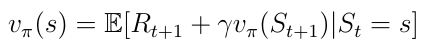
Eq.14分解的状态价值函数

相同的分解可以应用于动作价值函数：

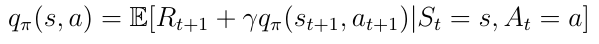
Eq.15分解的动作价值函数

在这里，我们讨论v（s）和q（s，a）如何相互关联。这些函数之间的关系可以用图表示：

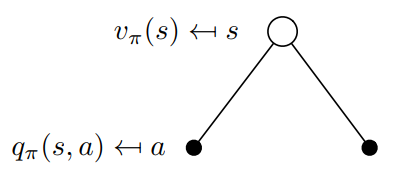
v（s）和 q（s，a）之间关系的可视化

在这个例子中，处于状态s允许我们采取两种可能的动作a。根据定义，在特定状态下采取特定动作会给我们动作价值q（s，a）。价值函数v（s）是在状态s中采取动作a的概率加权的可能q（s，a）的总和（等式16）。

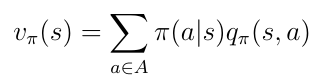
Eq.16状态价值函数等于动作价值的加权和

现在让我们考虑下图中的相反情况。二叉树的根现在是一个我们选择采取特定动作的状态。请记住，马尔可夫过程是随机的。采取动作并不意味着你会以100％的确定性达成想要的目标。严格地说，你必须考虑在采取动作后最终进入其他状态的概率。在采取动作a后，在特殊情况下，你可以以两种不同的状态s‘结束：

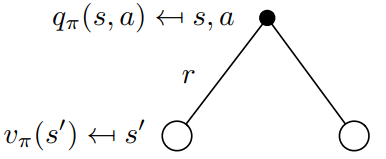
v（s）和 q（s，a）之间关系的可视化

要获得动作价值，必须采用由概率Pss'加权的折扣状态值，使其最终处于所有可能状态（本例中为2），并加上即时奖励：

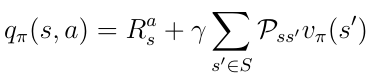
Eq.17q（s，a）和 v（s）之间的关系

现在我们知道了这些函数之间的关系，我们可以将公式16中的v（s）插入公式17中的q(s,a)。我们得到了公式 18，当前q（s，a）和下一个动作价值q（s'，a'）之间存在递归关系。

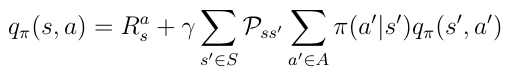
Eq.18动作价值函数的递归性质

这种递归关系可以再次在二叉树中可视化（如下图）。我们从q（s，a）开始，到达以一定概率Pss'的下一个状态s'，从那里可以采取带有概率π的动作a'，然后以动作价值q（s'， a'）结束。为了获得q（s，a），我们必须计算到“树冠”并求和所有概率，如公式18中所示

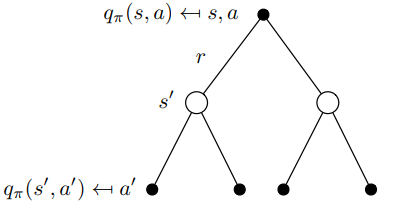
Eq.1q（s，a）的递归行为的可视化

3.5最优策略

深度强化学习中最重要的是找到最优的动作价值函数q *。找到q *表示智能体确切地知道任何给定状态下的动作的质量。此外，此外，代理可以决定必须采取的行动的质量。现在，我们定义q *的含义。最佳的动作价值函数是遵循最大化动作价值的策略的函数：

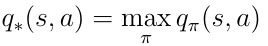
Eq.19最佳动作价值函数的定义

为了找到最好的策略，我们必须最大化q（s，a）。最大化意味着我们只选择q（s，a）具有最高值的所有可能动作中的动作a。因此，最优策略π定义如下：

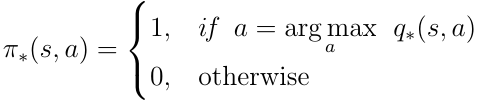
Eq.20最优策略。采取最大化q（s，a）的动作

3.6 贝尔曼最优方程

可以将最优策略的条件插入到公式18，贝尔曼最优方程：

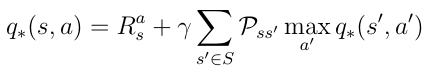
Eq.21贝尔曼最优方程

如果AI智能体可以解决这个方程，那么基本上意味着它解决了给定环境中的问题。智能体知道在任何给定的状态或情况下关于目标的任何可能动作的质量并且可以相应地表现。