人工智能无法逾越的一条鸿沟——哥德尔不完备性定理
2019年01月29日 由 荟荟 发表
773549
0
关于哥德尔定理的一些说明:
1.该定理并不意味着任何有趣的公理系统都是不完备的。例如,欧几里得几何可以被一阶公理化为一个完备的系统。
2.该定理需假设公理系统可以“定义”自然数。就算这些系统拥有包括自然数作为子集的模型,也不一定就能定义自然数。必须透过公理和一阶逻辑,在系统中表达出x是一个自然数这个概念才行。有许多系统包含自然数,却是完备的。例如,塔斯基(Tarski)证明了实闭域都是完备的一阶公理化系统。文中将不对此些误解作特殊解释。
2.如果系统S含有初等数论,当S无矛盾时,它的无矛盾性不可能在S内证明。”
什么意思呢?举个很常识的例子,小明把自己的日记藏在了"d盘-主题教育-核心价值观"文件内,那么在"核心价值观"文件夹内,小明可以对这些作品进行“修改名字”、“移动顺序”、“点开浏览”或者是“删除”等等操作,但小明在文件夹内,不能对这个文件夹本身进行操作,比如他不能在"核心价值观"文件夹内直接把"核心价值观"文件夹删掉。小明要想删除它,就必须到"主题教育"这一更高的层面去操作。(这里不解释“更高的层面”在数学上的理解。)这种性质叫做不完备性。
用更数学的话来说,这个定理允许了这样一个事实的存在:总有一些命题,在某一场合下,无法判断其真假性;换句话说,有些命题在某一场合下的真伪性不会对整个逻辑系统带来影响(但在更高的层面,这些命题或许就能被判断真假或者对逻辑系统带来影响了)。
人们会问:艾皮米尼地斯有没有说谎?这个悖论最简单的形式是:“我在说谎"。如果他在说谎,那么“我在说谎”就是一个谎,因此他说的是实话;但是如果这是实话,他又在说谎。矛盾不可避免。
这类悖论的一个标准形式是:如果事件a发生,则推导出非a,非a发生则推导出a,这是一个自相矛盾的无限逻辑循环。。。

在一切逻辑的悖论里都有一种“反身的自指”—— “它包含讲那个总体的某种东西,而这种东西又是总体中的一份子。因而这个命题所指涉的引证是命题本身,所以我们无从判断这个命题的真伪。这也是哥德尔不完备性定的另一种说法。

[真的不一定可证]。——没有任何公理系统可以证明它自身的相容性,任何可以证明自身相容性的公理系统都是不相容的。它甚至适用于计算机,这很可能意味着我们的思想也是不完备的。这个世上有许多观念我们永远无法了解,包括我们的思想是否具有相容性(我们的理性是否自相矛盾)。“没有人能够证明自己神志正常,因此,任何可以证明自己神志正常的人都是精神病人。”
伟大的德国作曲家巴赫, 以精美的赋格曲,卡农和严格的对位技巧著称于世。埃舍尔,画极红而人近无名,可谓荷兰的金海星。他极为善于营造一股逻辑诡异而奇幻的意境。作为两个相差了三百年的人, 巴赫和埃舍尔的作品有一个完美的结构相似性,”无穷上升“。
他们的无穷上升都是基于同一点的,自我重复,以至于自我涉及。而巴赫和埃舍尔不能想到的是,正是自我涉及这个概念,几近摧毁了整个二十世纪的数学。图灵机,停机问题,计算理论,蓬勃发展。以至于近期的人工智能。。。
机器要想具备自我模拟的能力,那么它首先要实现一个内嵌的虚拟世界。它好比一面镜子。可以映射真实世界里的东西,但它本身却比现实低了一个层级,所以它看起来更“假”。我们也可以从数据和程序的角度来理解:虚拟系统相对于真实机器来说就是数据。数据总是被动地由更加“真实”的机器所操纵。而且这种内嵌的虚拟层可以无限地延伸下去。也就是,我们可以在虚拟机上再安装虚拟机,以及虚拟机上的虚拟机……
好,当一台机器具备了内嵌虚拟层还不够,它还需要完成模拟自我的过程。也就是说,我们要让这台虚拟机器模拟它自己的运行动作。这在镜子的比喻中也就是我们要让镜子自己照自己。你很快就发现,这是不可能的。至少在镜子这个例子中,如果我们不借助外界(例如另一面镜子),这个镜子自身无法完成照射自己。
同样,在机器世界中,要让一台安装了模拟器的程序模拟自己,表面上看是不能完成的。不难想象,由于机器的内嵌虚拟层本身就是这台机器的一部分,于是,要想让虚拟层模拟机器自己的动作,就必须包括它的虚拟层,于是我们必须要有一个虚拟层的虚拟层。这样一来,我们就需要有无穷多的虚拟层,而且每一个虚拟层都要做同样的事情,模拟它上一层次的动作。你会发现,我们的机器很快便触及到了无穷多的虚拟层次,以至于怎么可能在有限的时间和空间内完成它呢?
还记得上文举得的几个例子嘛——谎言者悖论,圆,无穷上升的阶梯,无穷上升的巴赫赋格;反身自指,自我涉及。。。。。。
其实,人们早已发现这种巧妙地逃离这种无穷的方式。在计算机程序中,这叫做“蒯恩”程序。哥德尔用这种技巧完成了哥德尔定理的证明;图灵用这种技巧构造了图灵停机问题,指出了机器运算的极限;冯诺依曼用这种技巧制造了自复制的程序。我们同样可以用这种技巧构造可以模拟自身的程序。
在这里我想说明的是,这种被称为“蒯恩”的技巧,本质上讲可以实现这样的效果:执行一段包括蒯恩的模拟器就和将这个程序自己的源代码拿出来在模拟器上跑效果完全一致,所以它看起来就像在模拟自己(实际上我们没有任何手段能从运算结果上区分二者)。于是,我们便巧妙地绕过了无穷层次。
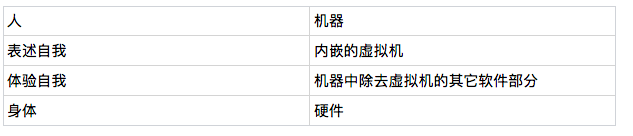
这种能够模拟自身运作的机器就可以算是具有自我觉知能力了。我们只需要将自模拟程序中的正在模拟自身的虚拟机理解成心理学里的“自我”,而将整个机器的其它部件都看作是体验自我和身体,那么这种自模拟程序就跟前文说到的人类的自我系统没有什么两样。
事实上,自我涉及到底能不能成为研究人工智能乃至同宇宙本身般复杂的人脑的捷径?从始至终。科学家还仍然找不到答案。。。
正如,我来到一个暗室,屋里似乎有个东西,虽然我摸得着,但是我看不见。
于是我买来一袋面粉,撒了上去,虽然我看不见那东西,但是我看得见面粉,于是我看到面粉勾勒出的形状,认为我看见了这个东西。
每一粒面粉就是一个例子,我们从无数的例子中勾勒出规则的样子罢了。
至于它为什么是这样?谁定的它?我不知道,我只会撒面粉……
文章转载至;https://www.zhihu.com/question/19554287/answer/16046997?utm_source=wechat_session&utm_medium=social&utm_oi=1061581829252997120
https://www.douban.com/group/topic/3057866/
http://www.360doc7.net/wxarticlenew/740624976.html
参考文献:【集异壁之大成】【超越无穷大】
1.该定理并不意味着任何有趣的公理系统都是不完备的。例如,欧几里得几何可以被一阶公理化为一个完备的系统。
2.该定理需假设公理系统可以“定义”自然数。就算这些系统拥有包括自然数作为子集的模型,也不一定就能定义自然数。必须透过公理和一阶逻辑,在系统中表达出x是一个自然数这个概念才行。有许多系统包含自然数,却是完备的。例如,塔斯基(Tarski)证明了实闭域都是完备的一阶公理化系统。文中将不对此些误解作特殊解释。
“如果有一天我能明白哥德尔的思想,我会很开心”

“1.任意一个包含一阶谓词逻辑与初等数论的形式系统,都存在一个命题,它在这个系统中既不能被证明为真,也不能被证明为否。
2.如果系统S含有初等数论,当S无矛盾时,它的无矛盾性不可能在S内证明。”
什么意思呢?举个很常识的例子,小明把自己的日记藏在了"d盘-主题教育-核心价值观"文件内,那么在"核心价值观"文件夹内,小明可以对这些作品进行“修改名字”、“移动顺序”、“点开浏览”或者是“删除”等等操作,但小明在文件夹内,不能对这个文件夹本身进行操作,比如他不能在"核心价值观"文件夹内直接把"核心价值观"文件夹删掉。小明要想删除它,就必须到"主题教育"这一更高的层面去操作。(这里不解释“更高的层面”在数学上的理解。)这种性质叫做不完备性。
用更数学的话来说,这个定理允许了这样一个事实的存在:总有一些命题,在某一场合下,无法判断其真假性;换句话说,有些命题在某一场合下的真伪性不会对整个逻辑系统带来影响(但在更高的层面,这些命题或许就能被判断真假或者对逻辑系统带来影响了)。
“也许问题的答案,就是问题的本身。存在的意义,就是存在的本身”
公元前六世纪,哲学家克利特人艾皮米尼地斯:“所有克利特人都说谎,他们中间的一个诗人这么说。”这就是这个著名悖论的来源。
人们会问:艾皮米尼地斯有没有说谎?这个悖论最简单的形式是:“我在说谎"。如果他在说谎,那么“我在说谎”就是一个谎,因此他说的是实话;但是如果这是实话,他又在说谎。矛盾不可避免。
这类悖论的一个标准形式是:如果事件a发生,则推导出非a,非a发生则推导出a,这是一个自相矛盾的无限逻辑循环。。。

在一切逻辑的悖论里都有一种“反身的自指”—— “它包含讲那个总体的某种东西,而这种东西又是总体中的一份子。因而这个命题所指涉的引证是命题本身,所以我们无从判断这个命题的真伪。这也是哥德尔不完备性定的另一种说法。

[真的不一定可证]。——没有任何公理系统可以证明它自身的相容性,任何可以证明自身相容性的公理系统都是不相容的。它甚至适用于计算机,这很可能意味着我们的思想也是不完备的。这个世上有许多观念我们永远无法了解,包括我们的思想是否具有相容性(我们的理性是否自相矛盾)。“没有人能够证明自己神志正常,因此,任何可以证明自己神志正常的人都是精神病人。”
“怪圈”
“圆”是个神奇的东西。人不知道它是什么。就取名为——“时间”。“圆”本是无始无终的。如果考虑你在圆圈上能行走的路径,那么圆圈就是一种无穷(递归)。圆形或椭圆形赛道是非常聪明的设计,因为你可以在上面进行任何长度的比赛。
伟大的德国作曲家巴赫, 以精美的赋格曲,卡农和严格的对位技巧著称于世。埃舍尔,画极红而人近无名,可谓荷兰的金海星。他极为善于营造一股逻辑诡异而奇幻的意境。作为两个相差了三百年的人, 巴赫和埃舍尔的作品有一个完美的结构相似性,”无穷上升“。
“巴赫赋格的无穷上升”

“埃舍尔画的无穷上升”

他们的无穷上升都是基于同一点的,自我重复,以至于自我涉及。而巴赫和埃舍尔不能想到的是,正是自我涉及这个概念,几近摧毁了整个二十世纪的数学。图灵机,停机问题,计算理论,蓬勃发展。以至于近期的人工智能。。。
“一种假设被提出——哥德尔机”

神奇的人工智能看似一个遥遥无期的梦,侯世达教授曾猜想,形式系统的自我涉及能不能成为人工智能的一个捷径?因为人脑无时无刻不在自我涉及,但是我们没有停机。。。。
“内嵌虚拟世界”
机器要想具备自我模拟的能力,那么它首先要实现一个内嵌的虚拟世界。它好比一面镜子。可以映射真实世界里的东西,但它本身却比现实低了一个层级,所以它看起来更“假”。我们也可以从数据和程序的角度来理解:虚拟系统相对于真实机器来说就是数据。数据总是被动地由更加“真实”的机器所操纵。而且这种内嵌的虚拟层可以无限地延伸下去。也就是,我们可以在虚拟机上再安装虚拟机,以及虚拟机上的虚拟机……
“模拟自我”
好,当一台机器具备了内嵌虚拟层还不够,它还需要完成模拟自我的过程。也就是说,我们要让这台虚拟机器模拟它自己的运行动作。这在镜子的比喻中也就是我们要让镜子自己照自己。你很快就发现,这是不可能的。至少在镜子这个例子中,如果我们不借助外界(例如另一面镜子),这个镜子自身无法完成照射自己。
同样,在机器世界中,要让一台安装了模拟器的程序模拟自己,表面上看是不能完成的。不难想象,由于机器的内嵌虚拟层本身就是这台机器的一部分,于是,要想让虚拟层模拟机器自己的动作,就必须包括它的虚拟层,于是我们必须要有一个虚拟层的虚拟层。这样一来,我们就需要有无穷多的虚拟层,而且每一个虚拟层都要做同样的事情,模拟它上一层次的动作。你会发现,我们的机器很快便触及到了无穷多的虚拟层次,以至于怎么可能在有限的时间和空间内完成它呢?
还记得上文举得的几个例子嘛——谎言者悖论,圆,无穷上升的阶梯,无穷上升的巴赫赋格;反身自指,自我涉及。。。。。。
其实,人们早已发现这种巧妙地逃离这种无穷的方式。在计算机程序中,这叫做“蒯恩”程序。哥德尔用这种技巧完成了哥德尔定理的证明;图灵用这种技巧构造了图灵停机问题,指出了机器运算的极限;冯诺依曼用这种技巧制造了自复制的程序。我们同样可以用这种技巧构造可以模拟自身的程序。
在这里我想说明的是,这种被称为“蒯恩”的技巧,本质上讲可以实现这样的效果:执行一段包括蒯恩的模拟器就和将这个程序自己的源代码拿出来在模拟器上跑效果完全一致,所以它看起来就像在模拟自己(实际上我们没有任何手段能从运算结果上区分二者)。于是,我们便巧妙地绕过了无穷层次。
这种能够模拟自身运作的机器就可以算是具有自我觉知能力了。我们只需要将自模拟程序中的正在模拟自身的虚拟机理解成心理学里的“自我”,而将整个机器的其它部件都看作是体验自我和身体,那么这种自模拟程序就跟前文说到的人类的自我系统没有什么两样。

事实上,自我涉及到底能不能成为研究人工智能乃至同宇宙本身般复杂的人脑的捷径?从始至终。科学家还仍然找不到答案。。。
“道可道非常道,名可名非常名”
哥德尔不完备性定理说明了“可证”与“真”不是同一个概念,“真”并不是只通过演绎就能达到的。即便是逻辑与数理中也需要要直觉(超验的信仰),人们最确信的知识也有着其本质上的不确定性。科学的可证伪性也说明了归纳知识的不确定性。我们对于这个世界只能基于表象给出一个合理的解释,然而却永远都不能确定它为什么是这样!
正如,我来到一个暗室,屋里似乎有个东西,虽然我摸得着,但是我看不见。
于是我买来一袋面粉,撒了上去,虽然我看不见那东西,但是我看得见面粉,于是我看到面粉勾勒出的形状,认为我看见了这个东西。
每一粒面粉就是一个例子,我们从无数的例子中勾勒出规则的样子罢了。
至于它为什么是这样?谁定的它?我不知道,我只会撒面粉……
文章转载至;https://www.zhihu.com/question/19554287/answer/16046997?utm_source=wechat_session&utm_medium=social&utm_oi=1061581829252997120
https://www.douban.com/group/topic/3057866/
http://www.360doc7.net/wxarticlenew/740624976.html
参考文献:【集异壁之大成】【超越无穷大】

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
美好的事物从跨越逻辑边界开始
热门企业
热门职位
写评论取消
回复取消






























