您尚未登录账户请先登录您的atyun账户，方可使用该功能
您的企业账号申请正在审核中审核通过后即可使用此功能，请耐心等待~
logistic回归的详细概述
2019年03月17日 由 sunlei 发表
230441
0
Logistic回归模型
Logistic回归在二十世纪初用于生物科学。 然后它被用于许多社会科学应用中。 当因变量（目标）是分类时，使用Logistic回归。
例如：
- 预测电子邮件是垃圾邮件（1）还是（0）
- 肿瘤是否恶性（1）与否（0）
考虑一种情况，我们需要对电子邮件是否为垃圾邮件进行分类。 如果我们对此问题使用线性回归，则需要根据可以进行的分类来设置阈值。 如果实际类别是恶性的，预测连续值为0.4且阈值为0.5，则数据点将被归类为非恶性，这可能导致实时严重后果。
从该示例中，可以推断线性回归不适合于分类问题。 线性回归是无界的，这使逻辑回归成为图像。 它们的值严格范围从0到1。
一、简单的Logistic回归
模型
输出= 0或1
假设=> Z = WX + B.
hΘ（x）= sigmoid（Z）
Sigmoid功能
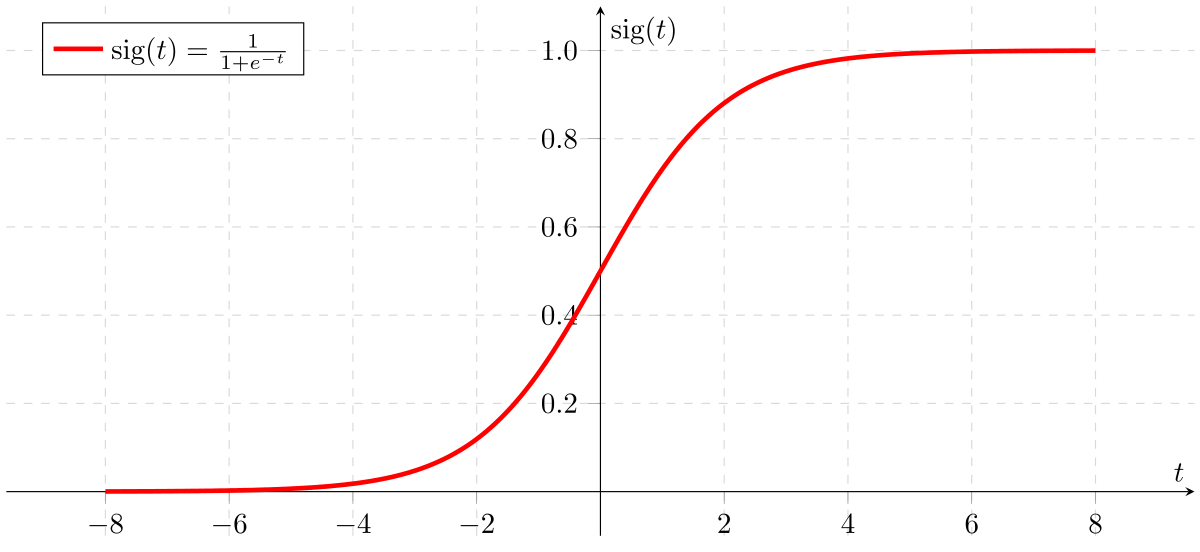
Sigmoid激活功能
如果'Z'变为无穷大，Y（预测）将变为1，如果'Z'变为负无穷大，Y（预测）将变为0。
分析假设
假设的输出是估计的概率。 这用于推断在给定输入X时预测值对实际值的信心。考虑以下示例，
X = [x0 x1] = [1 IP地址]
根据x1值，假设我们得到的估计概率为0.8。 这表明电子邮件有80％的可能性是垃圾邮件。
在数学上这可以写成：
这证明了“逻辑回归”的名称。 将数据拟合到线性回归模型中，然后通过预测目标分类因变量的逻辑函数对其进行操作。
二、Logistic回归的类型
二元Logistic回归
分类响应只有两个可能的结果。 示例：垃圾邮件与否
多项Logistic回归
三个或更多类别没有订购。 示例：预测哪种食物更受欢迎（蔬菜，非蔬菜，素食）
序数Logistic回归
订购时有三个或更多类别。 示例：电影评级从1到5
决策边界
要预测数据属于哪个类，可以设置阈值。 基于该阈值，将所获得的估计概率分类为类别。
比如说，如果predict_value≥0.5，则将电子邮件归类为垃圾邮件，而不是垃圾邮件。
决策边界可以是线性的或非线性的。 可以增加多项式阶数以获得复杂的决策边界。
成本函数
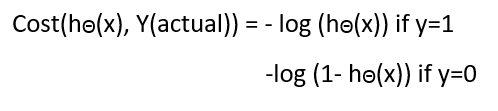
Logistic回归的成本函数
为什么用于线性的成本函数不能用于物流？
线性回归使用均方误差作为其成本函数。 如果这用于逻辑回归，则它将是参数（theta）的非凸函数。 只有当函数是凸的时，梯度下降才会收敛到全局最小值。
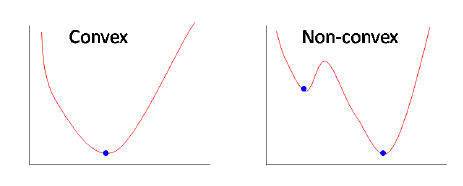
凸和非凸成本函数
成本函数说明
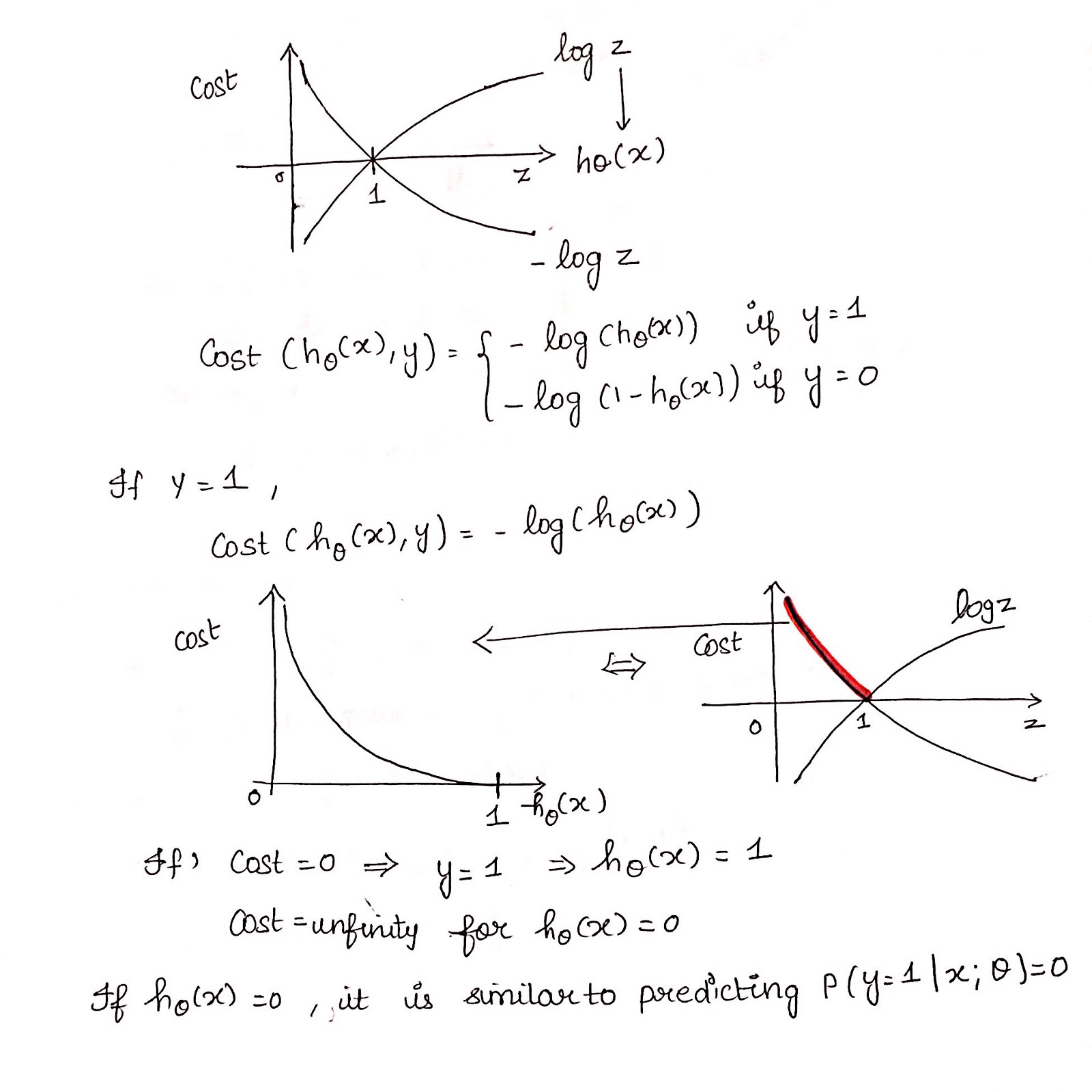
成本函数第1部分
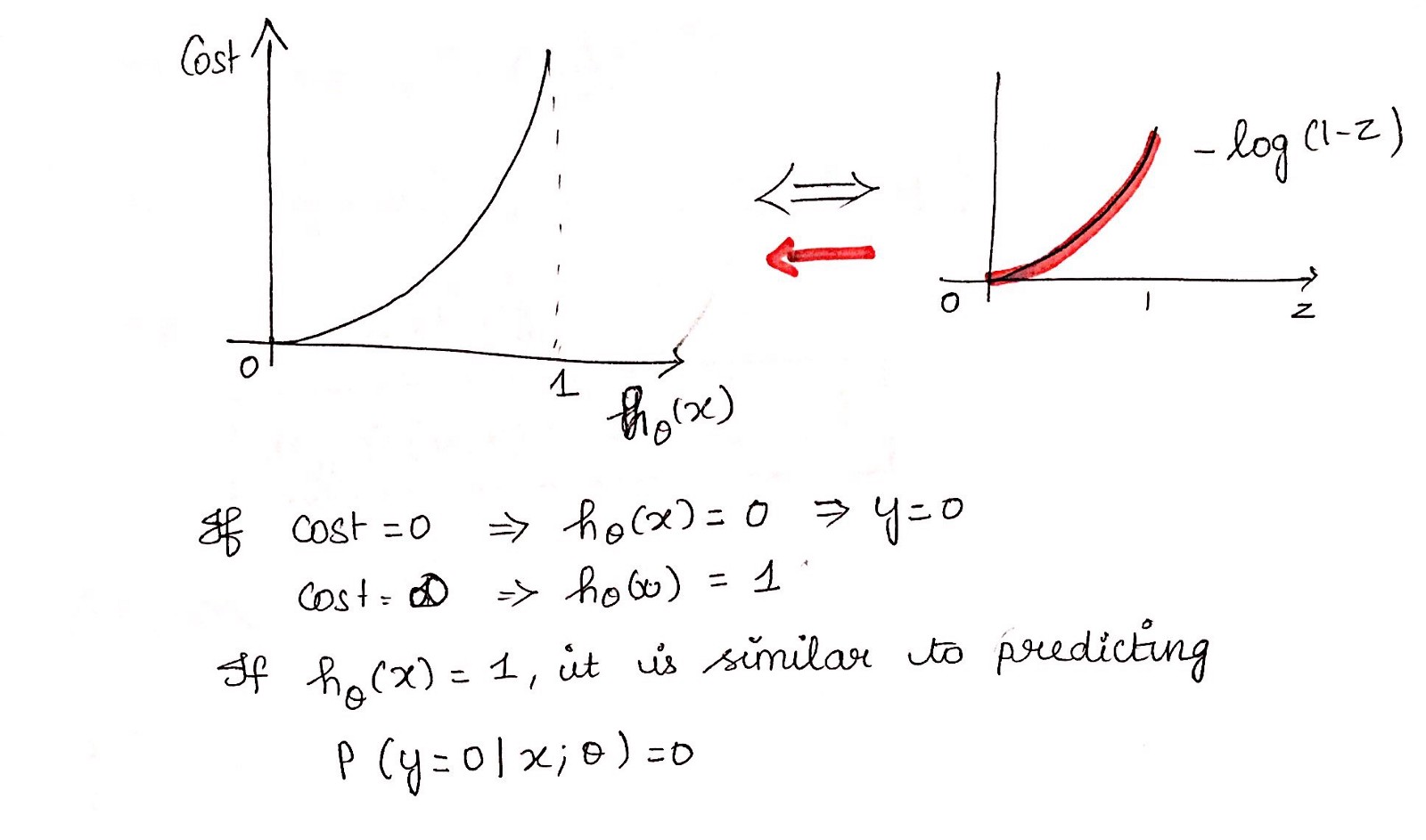
成本函数第2部分
简化的成本函数
简化的成本函数
公式的推导过程
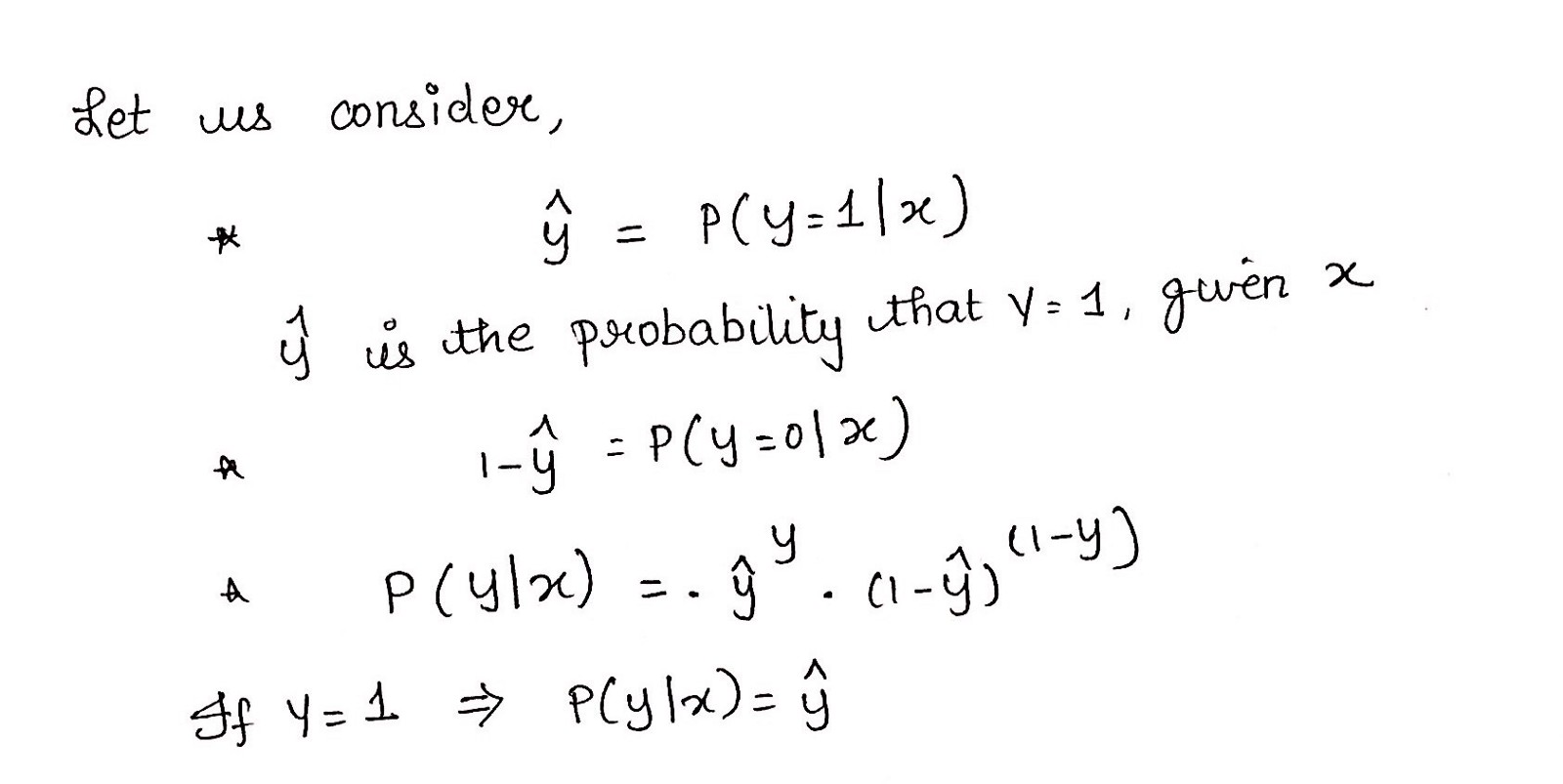
第1部分
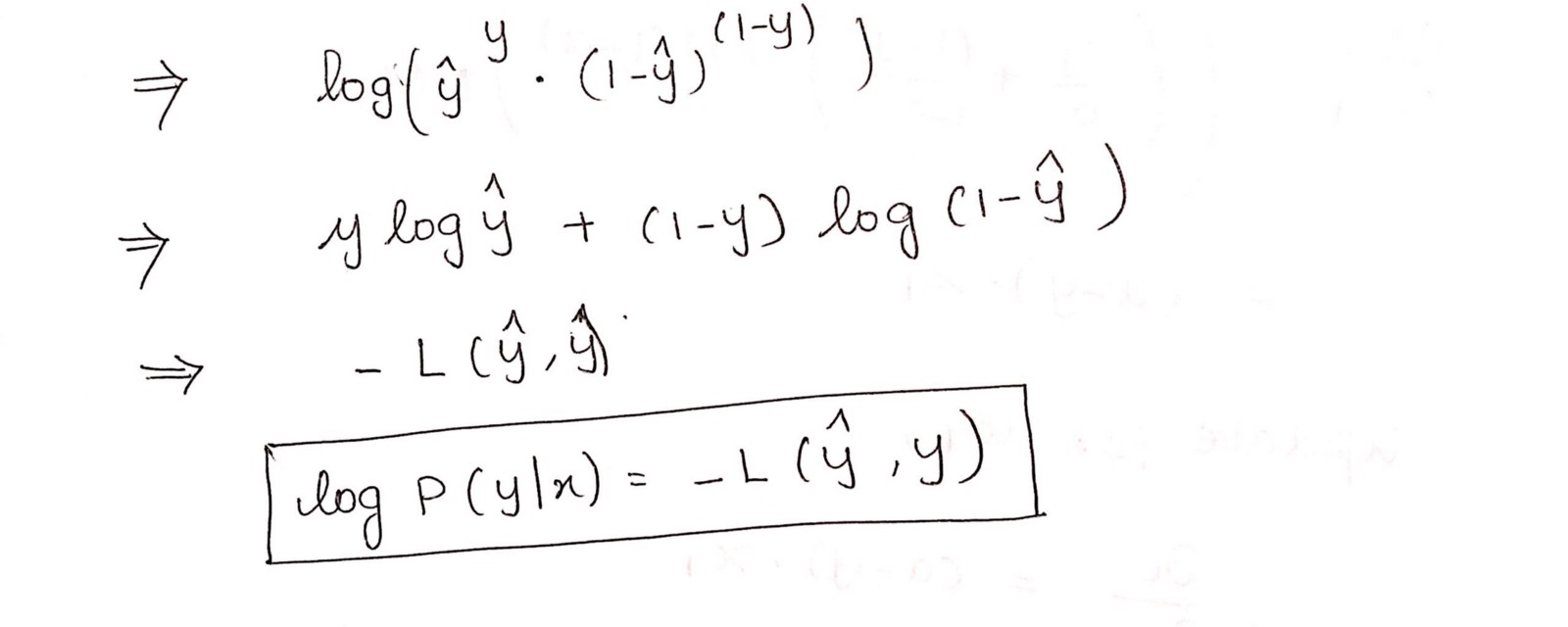
第2部分
这种负面作用是因为当我们训练时，我们需要通过最小化损失函数来最大化概率。 假设样本来自相同的独立分布，降低成本将增加最大可能性。
推导梯度下降算法的公式
算法第1部分
算法第2部分
Python实现
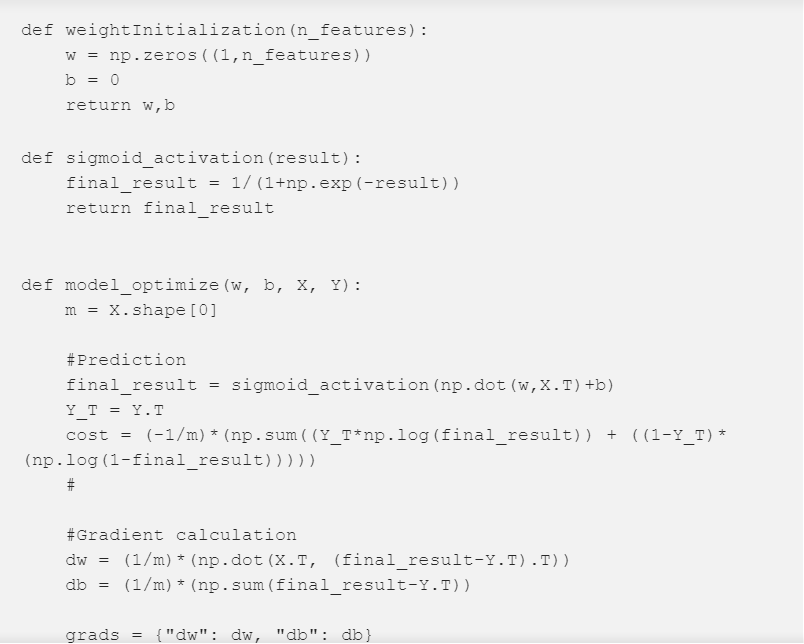
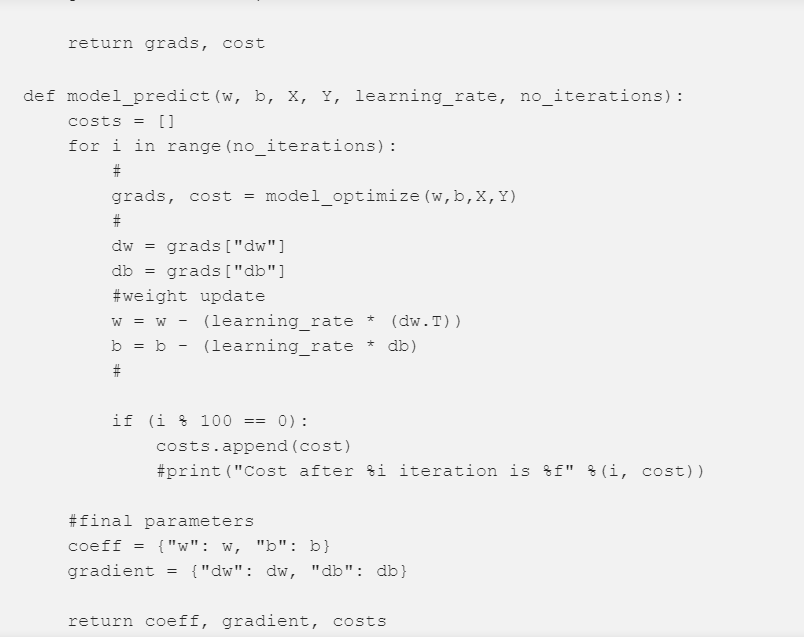
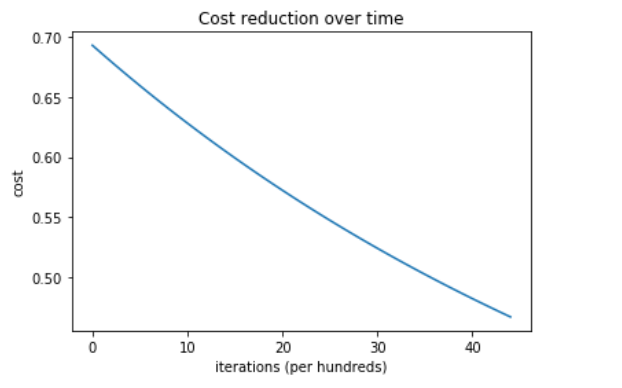
随时间降低成本和迭代次数
系统的训练和测试精度为100％
此实现用于二进制逻辑回归。 对于具有2个以上类别的数据，必须使用softmax回归。
欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
广告
广告
写评论取消
回复取消