学习K-Means算法:基于聚类的无监督机器学习算法
2019年03月16日 由 张江 发表
424711
0
 在本文中,我们将讨论K-Means算法,它是一种基于聚类的无监督机器学习算法。此外,我们还将讨论如何使用K-Means来压缩图像。
在本文中,我们将讨论K-Means算法,它是一种基于聚类的无监督机器学习算法。此外,我们还将讨论如何使用K-Means来压缩图像。在深入研究K-Means算法的细节之前,让我们先了解一下无监督的机器学习是什么,以及它的实际应用是什么。
与有标记数据的监督机器学习不同,,无监督机器学习处理未标记数据的问题。如果你熟悉经典的有监督机器学习,你可能会问,如何从未标记的数据集中学习任何有用的东西?成本函数是否不需要输出标签来计算算法的执行方式?
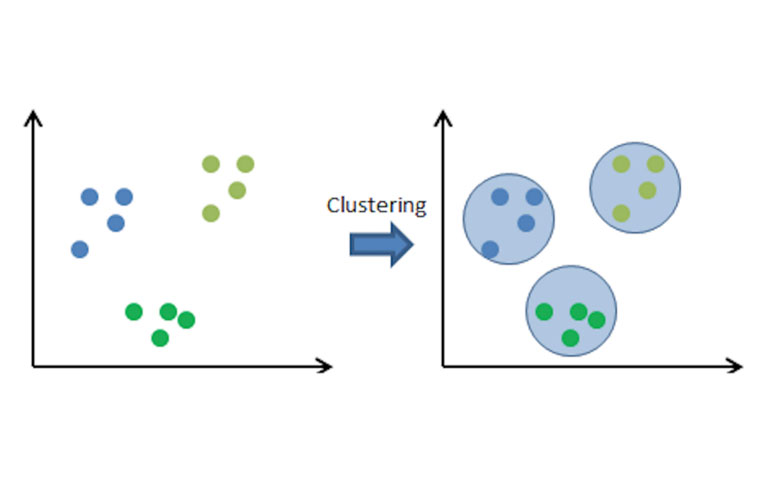
无监督机器学习(更具体地说是K-Means),是通过将相似的数据点聚集在高维空间中来实现的。
在左侧,数据点最初是分散的。假设我们不知道每个数据点是如何相关的,但它们不失普遍性。换句话说,仅仅通过查看图表,我们无法确定某某点是否相似,只是因为它们彼此靠近(同样,想象数据点是高维的,即大于3维)。
聚类的作用是,它将彼此更接近的数据点分组到一个聚类中,而不管维度的数量,从而表明属于单个聚类的数据点属于特定类。
这个简单的想法有可能解决我们社会面临的许多问题:
- 市场细分:根据不同的特征将潜在客户的市场划分或细分的过程。创建的细分市场由消费者组成,消费者将对营销策略做出类似响应,并且共享诸如类似兴趣,需求或位置等特征。
- 社交网络分析:分析具有相似品味的社交媒体平台的用户的过程。在识别具有相似品味的用户之后,运行有针对性的广告变得更容易。
- 天文数据分析:分析未标记的天文数据以找出隐藏模式的过程。
注意:你可能会惊讶地听到这个事实,但是当今世界中标记数据的数量只是可用数据量的一小部分。因此,这一事实进一步增强了无监督机器学习的优势。
K-Means算法
1.选择K,这是聚类的数量。虽然我们讨论的是无监督的机器学习,但算法并不会神奇地将输入数据集聚集到一定数量的聚类中。我们需要指定我们想要的聚类。基于领域知识,可以轻松指定所需的聚类。尽管如此,即使您不熟悉存在多少个聚类,也有一种技术可以确定如何选择“K”。
2.从所有可用数据点的集合中,随机选择K个数据点并将其称为“聚类质心”。
3.聚类分配。遍历整个数据集,对于每个数据点x(i),将其分配给它更接近的一个聚类质心。我们如何确定“近距离”?通过计算所述点之间的欧氏距离来做到这一点。现在,我们将形成聚类。我们将c(i)表示为最接近x(i)的聚类质心的索引。
4.移动质心。将聚类质心移动到另一个位置,该位置由它们所属的聚类中的点的平均值(即聚类内所有点的位置的平均值)确定。
5.连续重复步骤3和4,直到移动质心步骤没有任何显著变化。
实施K-Means
我们将使用以下关于汽车的数据集来执行聚类(从Kaggle下载):
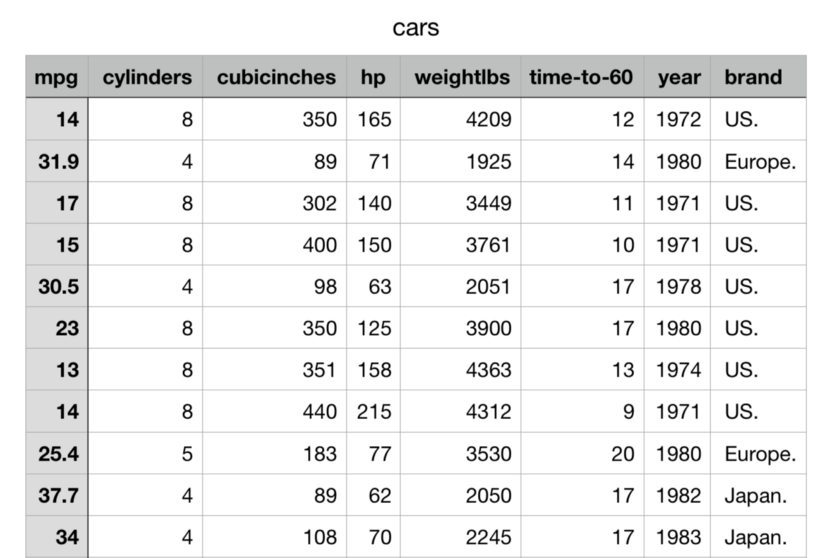
为了全面了解数据集,让我们查看seaborn配对图:
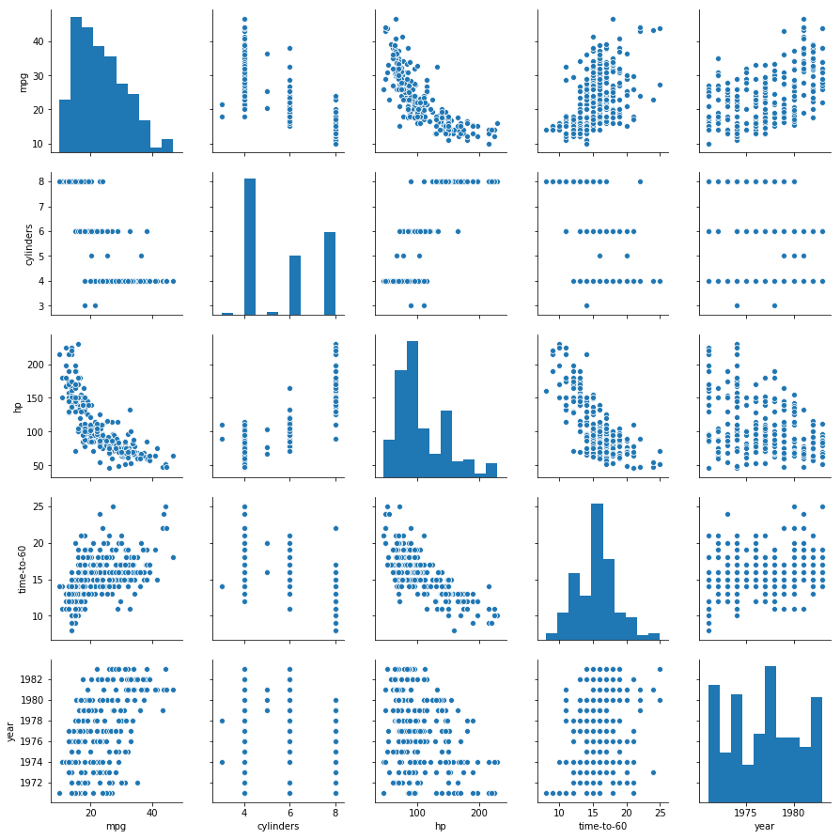
运行K-Means的整个代码库(以及上面的数据集)在Github存储库中,可以作为IPython笔记本使用:
github.com/adityachandupatla/ml_algorithms/blob/master/k_means/k-means.ipynb
我们在K-Means中用来确定聚类有多好的成本函数称为失真成本函数。本质上,它是数据点与分配给它的聚类质心的平均距离。
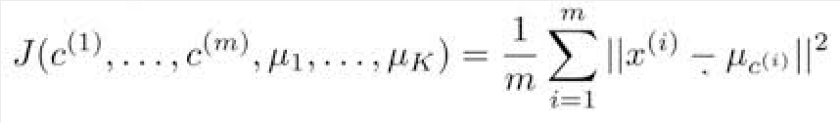
为了可视化聚类,请从cars.csv文件的可用列中取出两列。下面的可视化通过使用“hp”和“mpg”列完成的(但是,你可以自由选择任意数量的列):
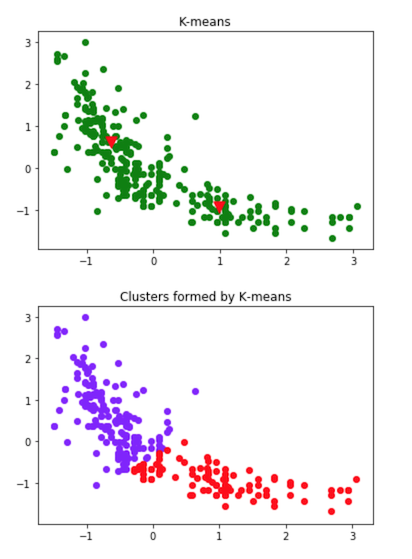
1.K = 2
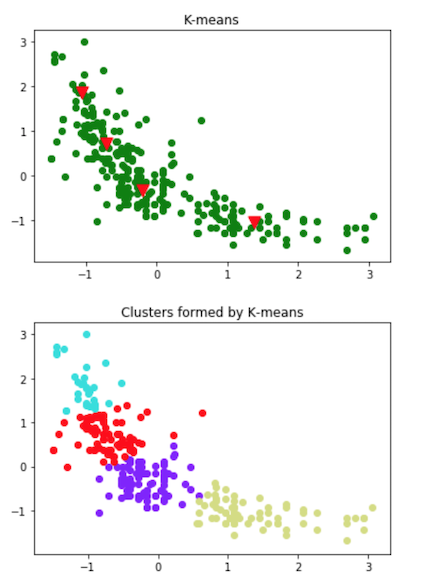
2. K = 4
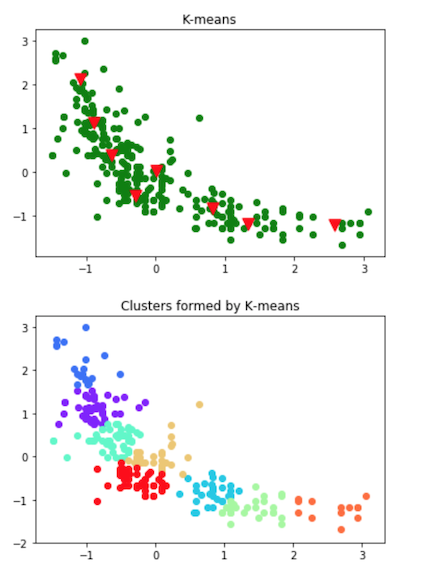
3. K = 8
4. K = 16
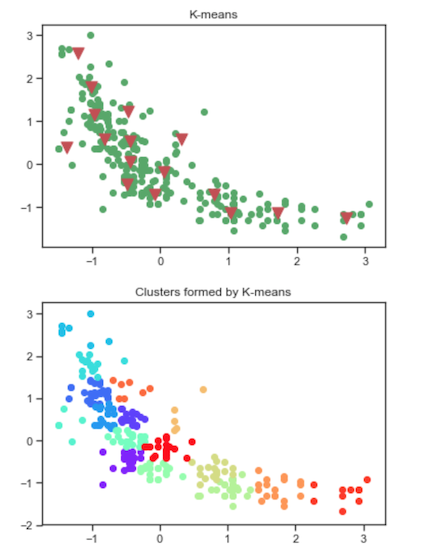
在上述图中,第一个图显示了数据集,以及聚类质心的最终位置(表示为三角形)。下一个图显示了结果聚类。我们可以看到,数据集似乎有大约2-4个聚类。为什么只有2-4个聚类,为什么不是8个或16个聚类?通过查看图,我们可以很容易看出K=8和K=16是冗余的,试图将足够接近的数据聚在一起。
这种说法似乎很直观。但是,如果我们的数据集是高维的呢?如果我们无法将其绘制在2D平面上,并想象K-Means中“K”的选择是对还是错,该怎么办?下一节将讨论这一问题。
选择K-Means中的K
在不依赖于领域知识或可视化的情况下,选择K的方法是采用elbow method。
我们用不同的 K 值运行K-Means几次(即首先只有一个聚类质心,然后是两个,以此类推)。对于每次运行,收集成本函数的输出并将其绘制在针对K的图形上。随着K增加,我们观察到成本函数J()也减小了。但过了一段时间后,在K = 3或4以后,K开始慢慢减少。你会得到一个看起来像肘部的图表:
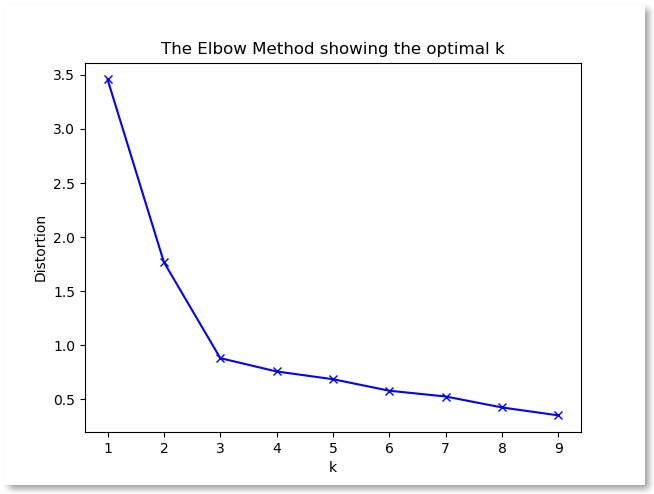
根据经验,肘点对应于K的最佳值。
使用K-Means进行图像压缩
是时候测试我们对K-Means的知识并将其应用于解决现实生活中的问题了。我们将使用K-Means来执行图像压缩。

最左边的图像描绘了实际图像。中间图像描绘了一个压缩图像,但剩下一点点分辨率。最右边的图像描绘了高度压缩和低分辨率的图像。压缩已经使用K-Means完成。
考虑你有一个大小为128 X 128 X 3的图像。如果你矢量化图像,你将有一个大小为16384 X 3的numpy数组。我们可以将这个图像视为数字数据的数据点,即我们必须忽略这个事实这个数据代表一个图像。
更具体地说,你可以将其视为任何其他大小为16384 X 3的numpy数组,其中示例的总数为m = 16384,并且要素的总数为n = 3。如果我们将K-Means应用于此数据集,通过选择让我们说K = 16,我们将选择16个最重要的数据点(这些数据点只是集群质心)。
如果我们现在将数组视为一个图像,唯一的区别是,我们现在只使用4位(因为2⁴= 16 = K)来表示图像颜色。新图像的总大小为:128 X 128 X 4 = 65536位。但是,我们仍然需要一些存储开销。我们仅使用4位来表示16种颜色。
但是,每种颜色(如果我们假设RGB格式)每个通道需要8位。换句话说,R + G + B = 8 + 8 + 8 = 24位以表示一种颜色。由于我们选择K = 16,对应16种颜色,我们额外需要24 X 16 = 384位。因此,表示新图像的总位数:65536 + 384 = 65920位。将其与原始图像进行比较,原始图像具有128 X 128像素,每个像素为24位颜色,结果是128 X 128 X 24 = 393216位。
显然,我们将图像压缩了6倍!结果惊人!
请记住,较高的K值意味着你不会大幅压缩图像,也就是说你将保留很多分辨率。但是,如果要选择较小的K值,则图像将被高度压缩,因此分辨率较低。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























