白话机器学习算法part4
2019年04月09日 由 sunlei 发表
642586
0
在前三部分中,我们已经讨论了梯度下降、线性回归和逻辑回归,决策树。
传送门:
白话机器学习算法part1
白话机器学习算法part2
白话机器学习算法part3
终于迎来了最终章,在最后这一部分我们讲一下随机森林。
随机森林可以说是最受初学者欢迎的数据科学集成模型。
 所以,集成模型只是许多模型的集合,就像我们前面所说的那样。
所以,集成模型只是许多模型的集合,就像我们前面所说的那样。
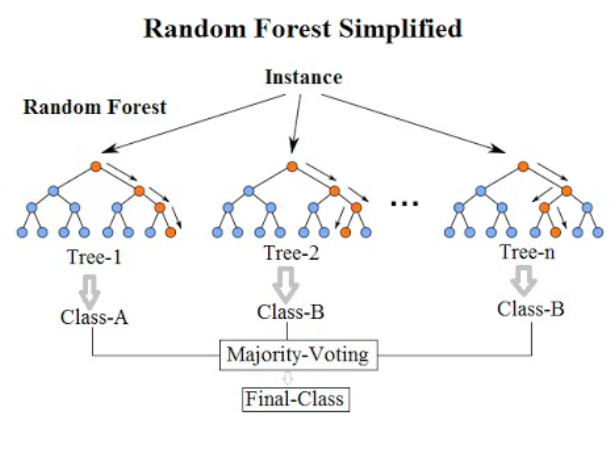
正如您上边的图表中看到的,像随机森林这样的集成模型只是一堆决策树。在这里,您可以看到有3个决策树。
利用袋装算法设计了随机森林等集合模型,以减少过度拟合和方差。
我们知道决策树很容易过度拟合。换句话说,一个决策树可以很好地为一个特定的问题找到一个解决方案,但是如果应用到一个以前从未见过的问题上,就相当糟糕了。与俗语“三个臭皮匠赛过诸葛亮”类似,集成模型使用许多擅长于其特定任务的决策树来生成一个更大的模型,它在许多不同的任务中都非常出色。以这种方式思考——你会通过听取单个员工的建议还是许多员工的建议来做出一个商业决策?可能是后者。决策树越多=越不适合。
在数据科学的世界里,我们需要对抗的的不仅仅是过度拟合。我们还必须反击所谓的方差。

具有“高方差”的模型是这样一种模型,如果它的输入即使是最微小的改变,其结果也会发生变化。就像过度拟合一样,这意味着高方差模型不能很好地推广新数据。
我喜欢考虑身体平衡方面的差异:如果你站在坚实的地面上单脚平衡,你就不会摔倒。但是如果突然有100英里/小时的阵风呢?我打赌你会摔倒的。这是因为你单腿平衡的能力在很大程度上取决于你周围环境的因素。即使有一件事改变了,也会把你搞得一团糟!这就是当模型具有高方差时的情况。如果我们把训练数据中的任一因素搞乱,我们就可以完全改变结果。这是不稳定的,因此不是一个我们想依靠它来做决定的模型。
在我们深入研究随机森林算法之前,有一件事我们还需要讨论,那就是学习者的想法。
在机器学习中,有弱学习者和强学习者,而bagging算法(或“Bootstrap聚集”算法)处理弱学习者。
弱学习者构成随机森林模型的主干。
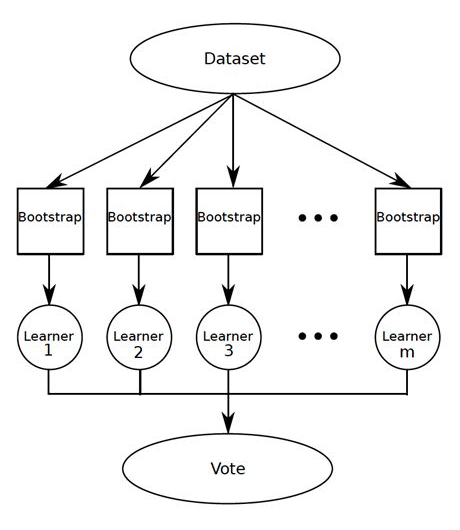
简单地说,弱学习者是预测/分类数据的算法,其准确性(或其他评估指标)略高于偶然性。这些家伙之所以有用,是因为我们可以将他们聚集在一起,形成一个更大的模型,其预测/分类的能力非常好!
像随机森林这样的集成模型使用袋装算法来避免高方差和过度拟合的陷阱,而像单个决策树这样的简单模型更容易陷入这种陷阱。

袋装算法的强大功能是,它们使用随机的数据样本进行替换。
这意味着,当算法通过随机的数据样本构建决策树时,没有数据点是它不能使用的。例如,仅仅因为一个决策树是由20个数据点构成的,并不意味着同样的20个数据点中的12个也不能构成另一个决策树。这就是概率!
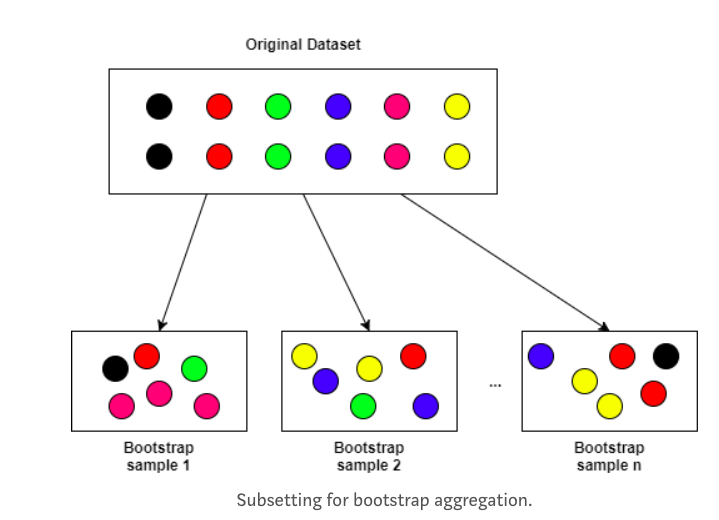
随机森林模型的一个很酷的地方是,它们可以同时(或以“并行”的方式)对每个决策树进行替换,从而完成所有这些随机抽样。因为我们处在随机抽样和替换的世界中,我们也可以假设我们的每一个决策树都是独立的。
总之:随机森林模型使用袋装算法来构建小决策树,每个决策树都与数据的随机子集同时构建。
但是,还有更多……
随机林模型中的每一棵树不仅只包含数据的一个子集,而且每一棵树也只使用数据中的一个子集特性(即列)。
例如,假设我们试图根据作者、出版日期、页数和语言将一本书归类为已售出或未售出。我们的数据集中有10000本书。在随机森林模型中,不仅我们的每一个决策树只使用10000本书的随机样本,而且每个决策树也只使用特征的随机样本:也许一个决策树会使用作者和出版日期,而另一个决策树会使用作者和页数。另外一个决策树可以使用语言和发布日期。重点是,当我们将所有这些决策树(即“弱学习者”)的预测平均在一起时,我们得到一个超级棒的预测!
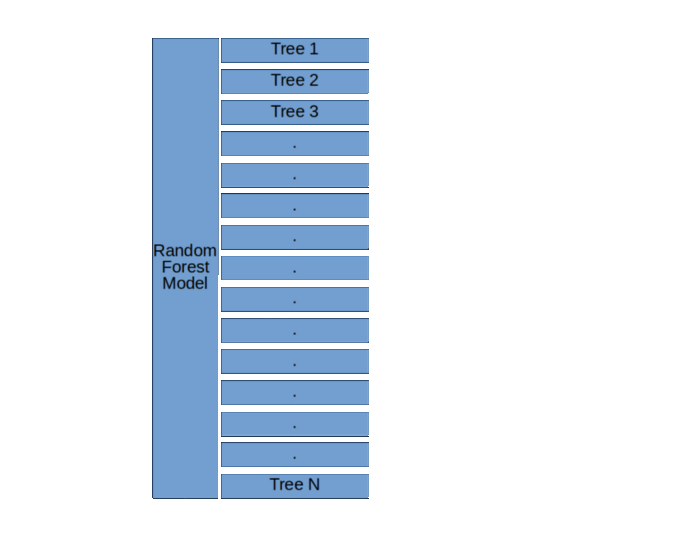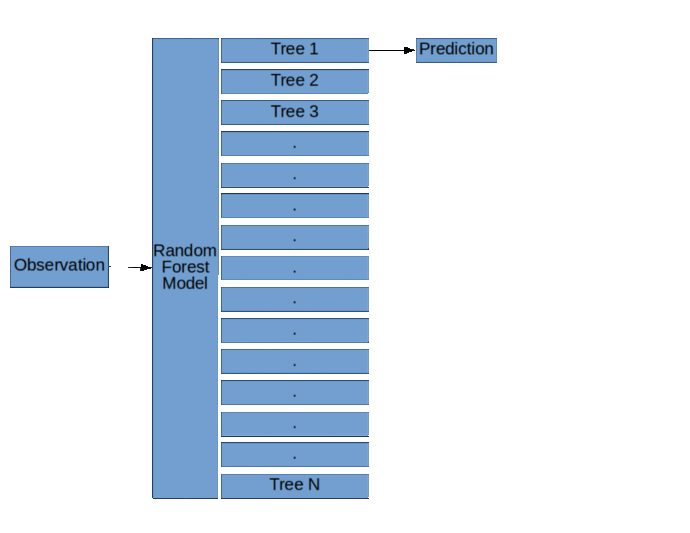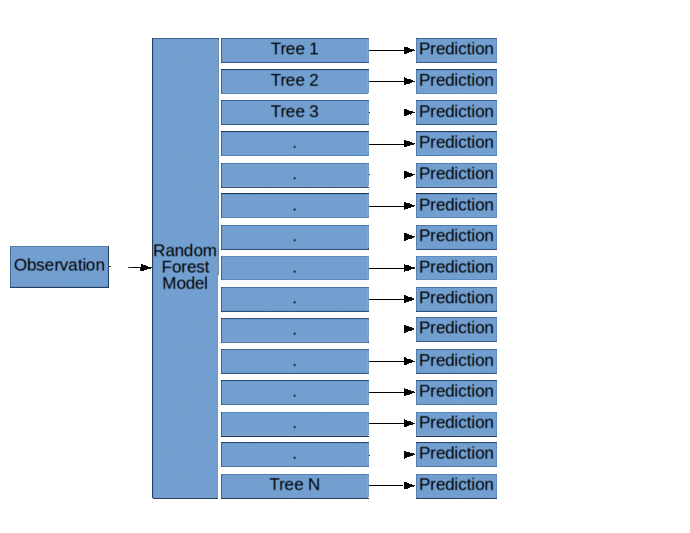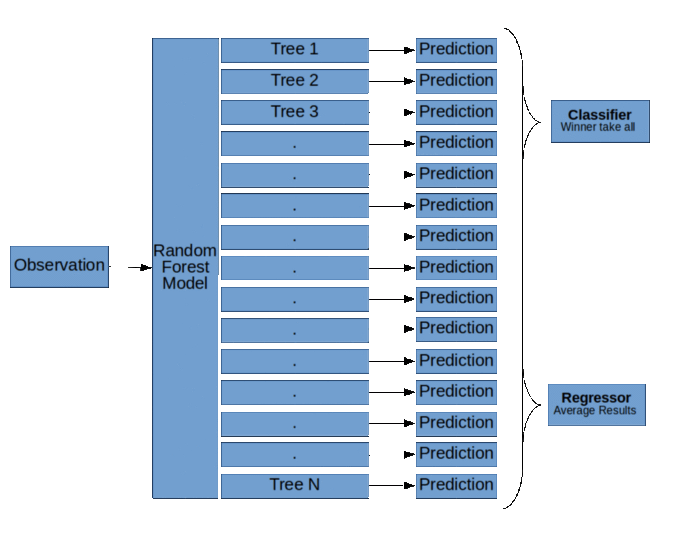
就是这样!当我们使用随机森林模型进行分类时,我们将所有决策树中的多数票作为结果。当我们使用随机森林模型进行回归时,我们平均每个决策树的所有概率,并使用该数字作为结果。
好了,我的这篇文章终于结束了。通过这篇文章,我们了解了决策树、非线性、过拟合和方差,以及随机森林等集成模型,希望对你们有用。
传送门:
白话机器学习算法part1
白话机器学习算法part2
白话机器学习算法part3
终于迎来了最终章,在最后这一部分我们讲一下随机森林。
Random Forest随机森林
随机森林可以说是最受初学者欢迎的数据科学集成模型。
 所以,集成模型只是许多模型的集合,就像我们前面所说的那样。
所以,集成模型只是许多模型的集合,就像我们前面所说的那样。
正如您上边的图表中看到的,像随机森林这样的集成模型只是一堆决策树。在这里,您可以看到有3个决策树。
利用袋装算法设计了随机森林等集合模型,以减少过度拟合和方差。
我们知道决策树很容易过度拟合。换句话说,一个决策树可以很好地为一个特定的问题找到一个解决方案,但是如果应用到一个以前从未见过的问题上,就相当糟糕了。与俗语“三个臭皮匠赛过诸葛亮”类似,集成模型使用许多擅长于其特定任务的决策树来生成一个更大的模型,它在许多不同的任务中都非常出色。以这种方式思考——你会通过听取单个员工的建议还是许多员工的建议来做出一个商业决策?可能是后者。决策树越多=越不适合。
在数据科学的世界里,我们需要对抗的的不仅仅是过度拟合。我们还必须反击所谓的方差。

具有“高方差”的模型是这样一种模型,如果它的输入即使是最微小的改变,其结果也会发生变化。就像过度拟合一样,这意味着高方差模型不能很好地推广新数据。
我喜欢考虑身体平衡方面的差异:如果你站在坚实的地面上单脚平衡,你就不会摔倒。但是如果突然有100英里/小时的阵风呢?我打赌你会摔倒的。这是因为你单腿平衡的能力在很大程度上取决于你周围环境的因素。即使有一件事改变了,也会把你搞得一团糟!这就是当模型具有高方差时的情况。如果我们把训练数据中的任一因素搞乱,我们就可以完全改变结果。这是不稳定的,因此不是一个我们想依靠它来做决定的模型。
Bagging 算法
在我们深入研究随机森林算法之前,有一件事我们还需要讨论,那就是学习者的想法。
在机器学习中,有弱学习者和强学习者,而bagging算法(或“Bootstrap聚集”算法)处理弱学习者。
Weak Learners弱学习者
弱学习者构成随机森林模型的主干。

简单地说,弱学习者是预测/分类数据的算法,其准确性(或其他评估指标)略高于偶然性。这些家伙之所以有用,是因为我们可以将他们聚集在一起,形成一个更大的模型,其预测/分类的能力非常好!
像随机森林这样的集成模型使用袋装算法来避免高方差和过度拟合的陷阱,而像单个决策树这样的简单模型更容易陷入这种陷阱。

袋装算法的强大功能是,它们使用随机的数据样本进行替换。
这意味着,当算法通过随机的数据样本构建决策树时,没有数据点是它不能使用的。例如,仅仅因为一个决策树是由20个数据点构成的,并不意味着同样的20个数据点中的12个也不能构成另一个决策树。这就是概率!

随机森林模型的一个很酷的地方是,它们可以同时(或以“并行”的方式)对每个决策树进行替换,从而完成所有这些随机抽样。因为我们处在随机抽样和替换的世界中,我们也可以假设我们的每一个决策树都是独立的。
总之:随机森林模型使用袋装算法来构建小决策树,每个决策树都与数据的随机子集同时构建。
但是,还有更多……
随机林模型中的每一棵树不仅只包含数据的一个子集,而且每一棵树也只使用数据中的一个子集特性(即列)。

例如,假设我们试图根据作者、出版日期、页数和语言将一本书归类为已售出或未售出。我们的数据集中有10000本书。在随机森林模型中,不仅我们的每一个决策树只使用10000本书的随机样本,而且每个决策树也只使用特征的随机样本:也许一个决策树会使用作者和出版日期,而另一个决策树会使用作者和页数。另外一个决策树可以使用语言和发布日期。重点是,当我们将所有这些决策树(即“弱学习者”)的预测平均在一起时,我们得到一个超级棒的预测!
就是这样!当我们使用随机森林模型进行分类时,我们将所有决策树中的多数票作为结果。当我们使用随机森林模型进行回归时,我们平均每个决策树的所有概率,并使用该数字作为结果。
好了,我的这篇文章终于结束了。通过这篇文章,我们了解了决策树、非线性、过拟合和方差,以及随机森林等集成模型,希望对你们有用。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























