揭秘反向传播算法,原理介绍与理解
2019年05月18日 由 bie管我叫啥 发表
88748
0
 机器学习最重要的一个方面是它能够识别输出中的误差范围,并能够在数据集越来越多的时候通过其神经网络提供更精确的数据解释。这通常称为反向传播,这个过程并不像想象中的那么复杂。
机器学习最重要的一个方面是它能够识别输出中的误差范围,并能够在数据集越来越多的时候通过其神经网络提供更精确的数据解释。这通常称为反向传播,这个过程并不像想象中的那么复杂。当人们听到“机器学习”这个术语时,他们首先想到的是类似于“Matrix”的东西,到处都是电脑掌控着世界。
但这些并不是机器学习和反向传播之类的东西。下面是对此的详细解释和探讨。
深度学习:神经网络,权重和偏见
神经网络只是一个非常复杂的机器:你把输入放进机器,然后得到一些输出。这台机器由多个任务组成,这样你就能最终得到你想要的东西。你还可以调整作为此过程一部分的每个任务,从而在最后获得最佳工作状态和最准确的结果。
在神经网络中,任务是隐层,任务性能的调整称为权重。这决定了如何考虑隐藏层中的每个节点,从而影响最终输出的结果。机器学习的原理是通过输入大量的数据集(如试错)来调整任务,最终获得最优的输出。
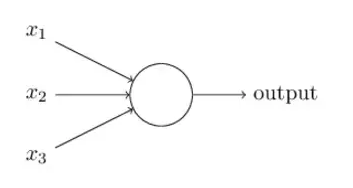
隐藏层中的节点如上图所示,这被称为感知器。我们可以看到有多个二进制输入产生单个二进制输出。现在我们已经解决了这个问题,是时候进行一些数学运算了(我保证这并不难)。
设X1,X2和X3表示输入,O表示输出。有两种不同的计算方法:
1.取输入的总和:O = X1 + X2 + X3。这个过程在考虑每个输入的同时,没有考虑到每个输入的重要性。你无法分辨其中一个输入如何影响另一个,只能知道它们各自如何影响结果。
2.应用线性函数运算:O =(X1 * X2)+ X3。这可能看起来很熟悉,那是因为它是线性函数的形式:y = mx + b。X1是输入,X2是权重,X3是偏差。这意味着X2决定了X1的重要性,因为它乘以X1。X2越接近0,它对输出的影响就越小。如果X1或X2 = 0,也有可能O = X3。在这种情况下,X3是偏置:它考虑的是不管输入是什么,这个输出将被激活多少。
你输出的结果是:
- 如果{weight * X +b≤0},则输出为0
- 如果{weight * X + b> 0},则输出为1
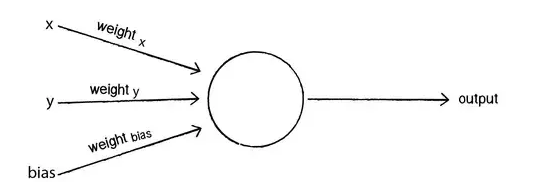
神经网络中的权重和偏差的原理可以在上图中看到:
- 如果{(X的权重)* X +(Y的权重)* Y + b> 0},则输出为1
- 否则输出等于0
输出的值是离散的:它是0或1。每个隐藏单元在应用其激活函数之前,可以被认为是多元线性回归。
什么是反向传播
很多时候,你会听到反向传播被称为优化技术:它是一种使用梯度下降的算法,以最大限度地减少机器学习模型预测中的误差。这将计算任何给定误差函数和人工神经网络的误差函数的梯度,同时考虑该神经网络内的不同权重。
梯度下降
梯度下降是一种算法,旨在最小化某个成本函数(错误的空间),因此输出是最准确的。但在开始训练之前,你需要拥有所有装备。
你需要了解您尝试最小化的功能(成本函数),其附加产品及其当前输入,权重和偏差,以便你可以获得所需的最准确的输出。你得到的回报是重量和偏差(参数)的值,误差幅度最小。
这是几乎每个ML模型中使用的算法。成本函数是用于查找机器学习模型预测中的错误的函数。通过微积分,函数的斜率是函数相对于值的导数。相对于一个权重的坡度,你知道到达山谷最低点所需的方向。迭代数据时,需要计算每个权重的斜率。通过权重的平均值,可以知道需要调整每个权重的位置从而获得最小的标准偏差。
要了解多少你实际需要调整重量,使用的是学习率,这被称为超参数。这基本上都是反复试验,通过为神经网络提供更多数据集来改进。如果梯度下降算法正常工作,则每次迭代的成本函数也应该减少。当它不再减少时,它已经会聚了。
反向传播总和
如前所述,权重之和可用z = a + b + c + d + ...表示,其中z是输出,a,b,c和d ......是加权输入。
我们想知道当我们调整网络中的权重时,误差会改变多少,这可以通过斜率找到。两个神经元a和b之间的误差范围和加权连接可以通过以下表达式表示:
∂error /∂a=(∂z/∂a)*(∂error/∂z)
对于z = a + b + c + d + ...,其导数为1,这意味着当其中一个输入元素增加1时,输出z也增加1。
反向传播Sigmoid函数
Sigmoid是代表S形曲线的词。就机器学习而言,这条曲线显示了每个权重对节点输出的影响,如下所示:
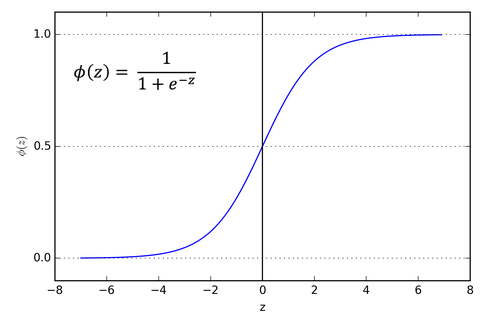
x轴表示输入的值,y轴表示该特定加权节点的输出值。
在x = 0时,函数的输出为y = 0.5。Sigmoid函数总是给出y值或节点的加权输出,介于0和1之间。请记住,加权输出是指隐藏层内的输出,而不是神经网络本身的最终输出。
为了反向传播sigmoid函数,我们需要找到它的方程的导数。如果a是输入神经元而b是输出神经元,则等式为:
b = 1 /(1 + e ^ -x)=σ(a)
这个特殊的函数有一个属性,你可以将1减去它自己在乘以它得到它的导数,如下所示:
σ(a)*(1 - σ(a))
你也可以解析分析并计算它。
反向传播修正线性单元(ReLU)
权重的影响也可以通过一个修正的线性函数来表示。这意味着所有的负权值都被认为是0。
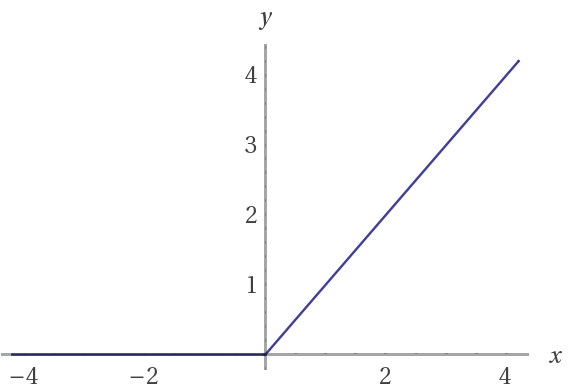
虽然感知器具有0或1的离散值,而sigmoid神经元具有从0到1的连续值,但是经修正的线性单元仅返回正值,因此由其参数的正部分定义。其值范围从0到无穷大。与sigmoid函数类似,修正线性单元的图形将x轴显示为输入值,并且将y轴显示为该特定加权节点的输出值。
如果a是加权输入而b是加权输出:当a> 0时b = a,否则b = 0。然后当a> 0时,等式的导数等于1,否则导数等于0。
总结
既然你已经了解了机器学习中反向传播的一些主要原则,那么你就会明白如何让技术变为现实,它教机器思考,正确识别趋势,并预测分析领域内的行为。降低机器学习预测的错误率可提高其准确性,使其超越任何人的能力。由于其应用范围广泛,这具有很大的现实意义,并且有巨大的机会发展到远远超出它现在所能做的。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
决策树完全指南(上)
热门企业
热门职位
写评论取消
回复取消






























