TensorFlow:如何通过声音识别追踪蝙蝠
2017年08月07日 由 yining 发表
830717
0
在之前的教程中,我们利用TensorFlow的Object Detector API训练了浣熊检测器实例, 如何用TensorFlow的Object Detector API来训练你的物体检测器,在这篇文章中,我将向你展示如何使用TensorFlow构建一个真正的通过声音来追踪蝙蝠位置的探测器。


为了解决这个问题,我把蝙蝠探测器连接到我的笔记本电脑上,并录下了几段视频。在一个分离的Jupyter notebook上,我创建了一个Labeling程序。这个程序创造了一秒钟的“声音片段”,我把它分为两种,一种包含蝙蝠的声音,另一种则不包含蝙蝠。我用数据和标签创建一种可以区分它们的分类器。
我导入了一些非常有用的库,Tensorflow、Keras和scikit,以便能构建一个声音识别管道。我喜欢的一个特定于声音的库是librosa,它可以帮助我加载和分析数据。
[1]:
在数据标签notebook中,我们键入标签,并将soundbytes(一款影音图像类软件)保存到我们键入的文件夹中。通过加载这些文件夹,我可以得到蝙蝠声音和非蝙蝠声音的文件。这个数据加载过程可能需要很长时间,取决于声音文件的数量。
我把所有的文件都上传到了Google云平台上。
注意,这个notebook本身也可以从它的Git仓库中下载。显然,在Jupyter notebook上的声音比在wordpress/medium上的声音更大。
[2]:
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a2.wav"][/audio]
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a0.wav"][/audio]
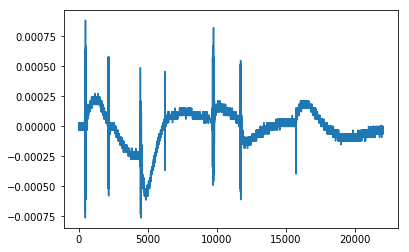
当你用耳机听蝙蝠声音的时候,可以听到一个清晰的声音。Librosa库可以执行傅立叶变换,提取由其组成的声音的频率。在构建任何机器学习算法之前,仔细检查所处理的数据是非常重要的。在这种情况下,我决定:
[3]:
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a2-2.wav"][/audio]
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a0.wav"][/audio]
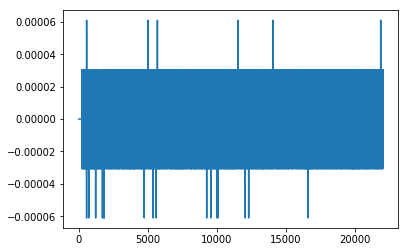

首先需要注意的是,我们所处理的数据并不是大数据。只有大约100个正面样本,深度神经网络很可能在这个daa指令上过于合适。我们正在处理的一个问题是,我们很容易收集到负面样本(仅仅记录没有蝙蝠一整天),并且很难收集到正面样本(因为蝙蝠每天只在这里呆上大约10-20分钟,需要手动标记数据)。当我们决定如何对数据进行分类时,需要考虑少量的正面样本。
正如我们可以看到的,信号的振幅是低噪音的,而信号具有高振幅。但是,这并不意味着所有的声音都是蝙蝠发出的。在这个频率下,你还可以获取其他的声音,比如揉搓手指或者电话信号。我决定把所有的负信号都放到一个大的“负极”的堆里,把电话信号,手指发出的噪音,和其他的东西放到一个更大的堆里。
我希望能看到蝙蝠在声谱图中产生的确切频率。不幸的是,我的传感器把它当成噪音超过了所有的频率。在声谱图上,你仍然可以看到声音和噪音之间的明显区别。我的第一个尝试是使用这个谱图作为卷积神经网络的输入。然而,仅仅使用了几个正面样本,就很难对这个网络进行训练了。因此,我放弃了这种方法。
最后,我决定采用一种“元数据方法”。我把声音的每一秒都分为22个部分。对于每个部分,我确定了样本的最大、最小、平均、标准差值。采用这种方法的原因是,“蝙蝠信号”在音频视觉化过程中显然不是高振幅信号。通过分析音频信号的不同部分,可以发现信号的多个部分是否具有某些特征(如高标准偏差),从而检测到蝙蝠的声音。
[4]:
就像每一个机器学习项目一样,建立一个输入-输出的管道是很重要的。我们定义了从声音文件中获取“元数据”的函数: 我们可以制作音频的声谱图,并简单地在音频数据中获取多个元特性的样本。下一步是将我们的预处理函数映射到训练和测试数据上。首先,我对每个音频样本应用一个预处理步骤,并将蝙蝠和非蝙蝠声音放在两个不同的列表中。之后,我加入了声音和标签。
在这种情况下,我们只能处理很少的“正面”样本和大量的负面样本。同时,将所有数据都标准化是一个非常好的想法。我的正面样本可能与正态分布不同,而且很容易被检测到。为了做到这一点,我使用了scikit learn预处理功能正常化的训练。在训练期间,我发现我对标准化和规范化的想法与scikit定义完全相反。在这种情况下,这可能不会是个问题,因为正常情况下,蝙蝠发出的声音可能仍然会产生不同的结果,而不是将噪声正常化。
[5]:
为了检测蝙蝠,我决定尝试一个非常简单的神经网络,它有三个隐藏的层。如果可训练的参数实在太少的话,网络只能区分声音的有无。如果有太多可训练的参数的话,网络将会轻易地覆盖我们所拥有的小数据集。
我决定在Keras中实现这个网络,它提供了在这个简单问题上轻松尝试不同的神经网络体系结构的最佳功能。
[6]:
在验证集的准确率达到95%的情况下,看起来我们做得还算不错。下一步是检查我们是否能在更长的音频中播放我们从未处理过的音频。
在蝙蝠几乎消失之后,我录了一段录音,我们看看能不能找到。
[7]:
[audio wav="https://www.atyun.com/uploadfile/2017/08/onedetectedbat.wav"][/audio]
最后,在26分钟的音频中,我的传感器检测到1只蝙蝠,但是当时可能没有蝙蝠(我无法证实这一点)。得出结论的是,我的程序是有效的!现在可以将这个程序集成到一个小的管道中,当外面有蝙蝠的时候会提醒我,或者可以每天做一个记录,测量蝙蝠的活动。


蝙蝠探测器
问题陈述
为了解决这个问题,我把蝙蝠探测器连接到我的笔记本电脑上,并录下了几段视频。在一个分离的Jupyter notebook上,我创建了一个Labeling程序。这个程序创造了一秒钟的“声音片段”,我把它分为两种,一种包含蝙蝠的声音,另一种则不包含蝙蝠。我用数据和标签创建一种可以区分它们的分类器。
库识别声音
我导入了一些非常有用的库,Tensorflow、Keras和scikit,以便能构建一个声音识别管道。我喜欢的一个特定于声音的库是librosa,它可以帮助我加载和分析数据。
[1]:
import random
import sys
import glob
import os
import time
import IPython
import matplotlib.pyplot as plt
from matplotlib.pyplot import specgram
import librosa
import librosa.display
from sklearn.preprocessing import normalize
import numpy as np
import tensorflow as tf
import keras
from keras.models import Sequential
from keras.layers import Dense, Conv2D, MaxPooling2D, Dropout, Flatten
Using TensorFlow backend.
用Python加载声音数据
在数据标签notebook中,我们键入标签,并将soundbytes(一款影音图像类软件)保存到我们键入的文件夹中。通过加载这些文件夹,我可以得到蝙蝠声音和非蝙蝠声音的文件。这个数据加载过程可能需要很长时间,取决于声音文件的数量。
我把所有的文件都上传到了Google云平台上。
- [Labeled sounds](https://storage.googleapis.com/pinchofintelligencebucket/labeled.zip)
- [Raw sounds](https://storage.googleapis.com/pinchofintelligencebucket/batsounds.zip)注意,这个notebook本身也可以从它的Git仓库中下载。显然,在Jupyter notebook上的声音比在wordpress/medium上的声音更大。
[2]:
# Note: SR stands for sampling rate, the rate at which my audio files were recorded and saved.
SR = 22050 # All audio files are saved like this
def load_sounds_in_folder(foldername):
""" Loads all sounds in a folder"""
sounds = []
for filename in os.listdir(foldername):
X, sr = librosa.load(os.path.join(foldername,filename))
assert sr == SR
sounds.append(X)
return sounds
## Sounds in which you can hear a bat are in the folder called "1". Others are in a folder called "0".
batsounds = load_sounds_in_folder('labeled/1')
noisesounds = load_sounds_in_folder('labeled/0')
print("With bat: %d without: %d total: %d " % (len(batsounds), len(noisesounds), len(batsounds)+len(noisesounds)))
print("Example of a sound with a bat:")
IPython.display.display(IPython.display.Audio(random.choice(batsounds), rate=SR,autoplay=True))
print("Example of a sound without a bat:")
IPython.display.display(IPython.display.Audio(random.choice(noisesounds), rate=SR,autoplay=True))
With bat: 96 without: 1133 total: 1229
Example of a sound with a bat:
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a2.wav"][/audio]
Example of a sound without a bat:
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a0.wav"][/audio]
可视化声音与Librosa
当你用耳机听蝙蝠声音的时候,可以听到一个清晰的声音。Librosa库可以执行傅立叶变换,提取由其组成的声音的频率。在构建任何机器学习算法之前,仔细检查所处理的数据是非常重要的。在这种情况下,我决定:
- 听声音
- 绘制声波
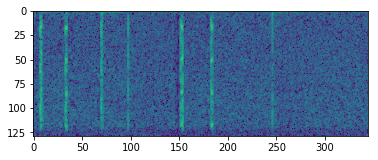
- 绘制时频谱(spectogram)(一段时间内频率振幅的可视化表示)。
[3]:
def get_short_time_fourier_transform(soundwave):
return librosa.stft(soundwave, n_fft=256)
def short_time_fourier_transform_amplitude_to_db(stft):
return librosa.amplitude_to_db(stft)
def soundwave_to_np_spectogram(soundwave):
step1 = get_short_time_fourier_transform(soundwave)
step2 = short_time_fourier_transform_amplitude_to_db(step1)
step3 = step2/100
return step3
def inspect_data(sound):
plt.figure()
plt.plot(sound)
IPython.display.display(IPython.display.Audio(sound, rate=SR))
a = get_short_time_fourier_transform(sound)
Xdb = short_time_fourier_transform_amplitude_to_db(a)
plt.figure()
plt.imshow(Xdb)
plt.show()
print("Length per sample: %d, shape of spectogram: %s, max: %f min: %f" % (len(sound), str(Xdb.shape), Xdb.max(), Xdb.min()))
inspect_data(batsounds[0])
inspect_data(noisesounds[0])
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a2-2.wav"][/audio]


Length per sample: 22050, shape of spectogram: (129, 345), max: -22.786959 min: -100.000000
[audio wav="https://www.atyun.com/uploadfile/2017/08/bats1.m4a0.wav"][/audio]


Length per sample: 22050, shape of spectogram: (129, 345), max: -58.154167 min: -100.000000
数据分析
首先需要注意的是,我们所处理的数据并不是大数据。只有大约100个正面样本,深度神经网络很可能在这个daa指令上过于合适。我们正在处理的一个问题是,我们很容易收集到负面样本(仅仅记录没有蝙蝠一整天),并且很难收集到正面样本(因为蝙蝠每天只在这里呆上大约10-20分钟,需要手动标记数据)。当我们决定如何对数据进行分类时,需要考虑少量的正面样本。
音频信号
正如我们可以看到的,信号的振幅是低噪音的,而信号具有高振幅。但是,这并不意味着所有的声音都是蝙蝠发出的。在这个频率下,你还可以获取其他的声音,比如揉搓手指或者电话信号。我决定把所有的负信号都放到一个大的“负极”的堆里,把电话信号,手指发出的噪音,和其他的东西放到一个更大的堆里。
声谱图
我希望能看到蝙蝠在声谱图中产生的确切频率。不幸的是,我的传感器把它当成噪音超过了所有的频率。在声谱图上,你仍然可以看到声音和噪音之间的明显区别。我的第一个尝试是使用这个谱图作为卷积神经网络的输入。然而,仅仅使用了几个正面样本,就很难对这个网络进行训练了。因此,我放弃了这种方法。
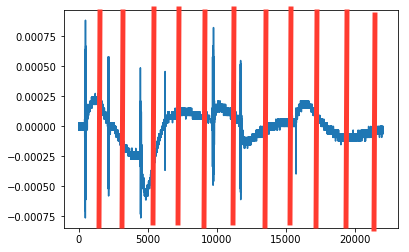
最后,我决定采用一种“元数据方法”。我把声音的每一秒都分为22个部分。对于每个部分,我确定了样本的最大、最小、平均、标准差值。采用这种方法的原因是,“蝙蝠信号”在音频视觉化过程中显然不是高振幅信号。通过分析音频信号的不同部分,可以发现信号的多个部分是否具有某些特征(如高标准偏差),从而检测到蝙蝠的声音。

[4]:
WINDOW_WIDTH = 10
AUDIO_WINDOW_WIDTH = 1000 # With sampling rate of 22050 we get 22 samples for our second of audio
def audio_to_metadata(audio):
""" Takes windows of audio data, per window it takes the max value, min value, mean and stdev values"""
features = []
for start in range(0,len(audio)-AUDIO_WINDOW_WIDTH,AUDIO_WINDOW_WIDTH):
subpart = audio[start:start+AUDIO_WINDOW_WIDTH]
maxval = max(subpart)
minval = min(subpart)
mean = np.mean(subpart)
stdev = np.std(subpart)
features.extend([maxval,minval,mean,stdev,maxval-minval])
return features
metadata = audio_to_metadata(batsounds[0])
print(metadata)
print(len(metadata))
[0.00088500977, -0.00076293945, 6.7962646e-05, 0.00010915515, 0.0016479492, 0.0002746582, 3.0517578e-05, 0.0001790466
3, 5.4772983e-05, 0.00024414062, 0.00057983398, -0.00057983398, -2.8137207e-05, 8.1624778e-05, 0.001159668, -9.1552734
e-05, -0.0002746582, -0.00019345093, 3.922523e-05, 0.00018310547, 0.00048828125, -0.00076293945, -0.00036187744, 0.000
15121402, 0.0012512207, -3.0517578e-05, -0.00057983398, -0.00027001952, 0.00015006117, 0.00054931641, 0.00045776367, -
0.00036621094, 5.9234619e-05, 5.0381914e-05, 0.00082397461, 0.00015258789, 6.1035156e-05, 0.00011447143, 1.7610495e-0
5, 9.1552734e-05, 0.00015258789, 6.1035156e-05, 9.3963623e-05, 1.8880468e-05, 9.1552734e-05, 0.00082397461, -0.0004882
8125, 7.7423094e-05, 8.6975793e-05, 0.0013122559, 0.00021362305, 6.1035156e-05, 0.00014205933, 2.5201958e-05, 0.000152
58789, 0.00054931641, -0.00061035156, 2.8991699e-05, 9.5112577e-05, 0.001159668, -3.0517578e-05, -0.00018310547, -0.00
010638428, 2.9584806e-05, 0.00015258789, 3.0517578e-05, -9.1552734e-05, -2.7862548e-05, 2.323009e-05, 0.00012207031,
6.1035156e-05, -3.0517578e-05, 1.8341065e-05, 1.905331e-05, 9.1552734e-05, 0.00018310547, -0.00039672852, 4.9438477e-05, 4.7997077e-0
5, 0.00057983398, 0.00021362305, 9.1552734e-05, 0.00017184448, 2.1811828e-05, 0.00012207031, 0.00015258
789, -6.1035156e-05, 5.0659179e-05, 4.6846228e-05, 0.00021362305, 0.0, -0.00015258789, -5.4656983e-05, 2.7488175e-05,
0.00015258789, -3.0517578e-05, -0.00012207031, -9.0820315e-05, 1.7085047e-05, 9.1552734e-05, 0.0, -0.00012207031, -7.2
296141e-05, 1.917609e-05, 0.00012207031, 0.0, -9.1552734e-05, -4.4189452e-05, 1.8292634e-05, 9.1552734e-05]
110
数据管理
就像每一个机器学习项目一样,建立一个输入-输出的管道是很重要的。我们定义了从声音文件中获取“元数据”的函数: 我们可以制作音频的声谱图,并简单地在音频数据中获取多个元特性的样本。下一步是将我们的预处理函数映射到训练和测试数据上。首先,我对每个音频样本应用一个预处理步骤,并将蝙蝠和非蝙蝠声音放在两个不同的列表中。之后,我加入了声音和标签。
在这种情况下,我们只能处理很少的“正面”样本和大量的负面样本。同时,将所有数据都标准化是一个非常好的想法。我的正面样本可能与正态分布不同,而且很容易被检测到。为了做到这一点,我使用了scikit learn预处理功能正常化的训练。在训练期间,我发现我对标准化和规范化的想法与scikit定义完全相反。在这种情况下,这可能不会是个问题,因为正常情况下,蝙蝠发出的声音可能仍然会产生不同的结果,而不是将噪声正常化。
[5]:
# Meta-feature based batsounds and their labels
preprocessed_batsounds = list()
preprocessed_noisesounds = list()
for sound in batsounds:
expandedsound = audio_to_metadata(sound)
preprocessed_batsounds.append(expandedsound)
for sound in noisesounds:
expandedsound = audio_to_metadata(sound)
preprocessed_noisesounds.append(expandedsound)
labels = [0]*len(preprocessed_noisesounds) + [1]*len(preprocessed_batsounds)
assert len(labels) == len(preprocessed_noisesounds) + len(preprocessed_batsounds)
allsounds = preprocessed_noisesounds + preprocessed_batsounds
allsounds_normalized = normalize(np.array(allsounds),axis=1)
one_hot_labels = keras.utils.to_categorical(labels)
print(allsounds_normalized.shape)
print("Total noise: %d total bat: %d total: %d" % (len(allsounds_normalized), len(preprocessed_batsounds), len(allsounds)))
## Now zip the sounds and labels, shuffle them, and split into a train and testdataset
zipped_data = zip(allsounds_normalized, one_hot_labels)
np.random.shuffle(zipped_data)
random_zipped_data = zipped_data
VALIDATION_PERCENT = 0.8 # use X percent for training, the rest for validation
traindata = random_zipped_data[0:int(VALIDATION_PERCENT*len(random_zipped_data))]
valdata = random_zipped_data[int(VALIDATION_PERCENT*len(random_zipped_data))::]
indata = [x[0] for x in traindata]
outdata = [x[1] for x in traindata]
valin = [x[0] for x in valdata]
valout = [x[1] for x in valdata]
(1229, 110)
Total noise: 1229 total bat: 96 total: 1229
机器学习模型
为了检测蝙蝠,我决定尝试一个非常简单的神经网络,它有三个隐藏的层。如果可训练的参数实在太少的话,网络只能区分声音的有无。如果有太多可训练的参数的话,网络将会轻易地覆盖我们所拥有的小数据集。
我决定在Keras中实现这个网络,它提供了在这个简单问题上轻松尝试不同的神经网络体系结构的最佳功能。
[6]:
LEN_SOUND = len(preprocessed_batsounds[0])
NUM_CLASSES = 2 # Bat or no bat
model = Sequential()
model.add(Dense(128, activation='relu',input_shape=(LEN_SOUND,)))
model.add(Dense(32, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(2))
model.compile(loss="mean_squared_error", optimizer='adam', metrics=['mae','accuracy'])
model.summary()
model.fit(np.array(indata), np.array(outdata), batch_size=64, epochs=10,verbose=2, shuffle=True)
valresults = model.evaluate(np.array(valin), np.array(valout), verbose=0)
res_and_name = zip(valresults, model.metrics_names)
for result,name in res_and_name:
print("Validation " + name + ": " + str(result))
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 128) 14208
_________________________________________________________________
dense_2 (Dense) (None, 32) 4128
_________________________________________________________________
dense_3 (Dense) (None, 32) 1056
_________________________________________________________________
dense_4 (Dense) (None, 2) 66
=================================================================
Total params: 19,458
Trainable params: 19,458
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
0s - loss: 0.2835 - mean_absolute_error: 0.4101 - acc: 0.9237
Epoch 2/10
0s - loss: 0.0743 - mean_absolute_error: 0.1625 - acc: 0.9237
Epoch 3/10
0s - loss: 0.0599 - mean_absolute_error: 0.1270 - acc: 0.9237
Epoch 4/10
0s - loss: 0.0554 - mean_absolute_error: 0.1116 - acc: 0.9237
Epoch 5/10
0s - loss: 0.0524 - mean_absolute_error: 0.1071 - acc: 0.9237
Epoch 6/10
0s - loss: 0.0484 - mean_absolute_error: 0.1024 - acc: 0.9237
Epoch 7/10
0s - loss: 0.0436 - mean_absolute_error: 0.1036 - acc: 0.9329
Epoch 8/10
0s - loss: 0.0375 - mean_absolute_error: 0.0983 - acc: 0.9481
Epoch 9/10
0s - loss: 0.0327 - mean_absolute_error: 0.0923 - acc: 0.9624
Epoch 10/10
0s - loss: 0.0290 - mean_absolute_error: 0.0869 - acc: 0.9644
Validation loss: 0.0440898474639
Validation mean_absolute_error: 0.101937913192
Validation acc: 0.930894308458
检测管线的结果和实施
在验证集的准确率达到95%的情况下,看起来我们做得还算不错。下一步是检查我们是否能在更长的音频中播放我们从未处理过的音频。
在蝙蝠几乎消失之后,我录了一段录音,我们看看能不能找到。
[7]:
soundarray, sr = librosa.load("batsounds/bats9.m4a")
maxseconds = int(len(soundarray)/sr)
for second in range(maxseconds-1):
audiosample = np.array(soundarray[second*sr:(second+1)*sr])
metadata = audio_to_metadata(audiosample)
testinput = normalize(np.array([metadata]),axis=1)
prediction = model.predict(testinput)
if np.argmax(prediction) ==1:
IPython.display.display(IPython.display.Audio(audiosample, rate=sr,autoplay=True))
time.sleep(2)
print("Detected a bat at " + str(second) + " out of " + str(maxseconds) + " seconds")
print(prediction)
[audio wav="https://www.atyun.com/uploadfile/2017/08/onedetectedbat.wav"][/audio]
Detected a bat at 514 out of 669 seconds
[[ 0.45205975 0.50231218]]
结论
最后,在26分钟的音频中,我的传感器检测到1只蝙蝠,但是当时可能没有蝙蝠(我无法证实这一点)。得出结论的是,我的程序是有效的!现在可以将这个程序集成到一个小的管道中,当外面有蝙蝠的时候会提醒我,或者可以每天做一个记录,测量蝙蝠的活动。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
上一篇
评估Keras深度学习模型的性能
热门企业
热门职位
写评论取消
回复取消






























