Winograd快速卷积解析
2019年07月27日 由 sunlei 发表
690551
0
[caption id="attachment_42342" align="aligncenter" width="770"]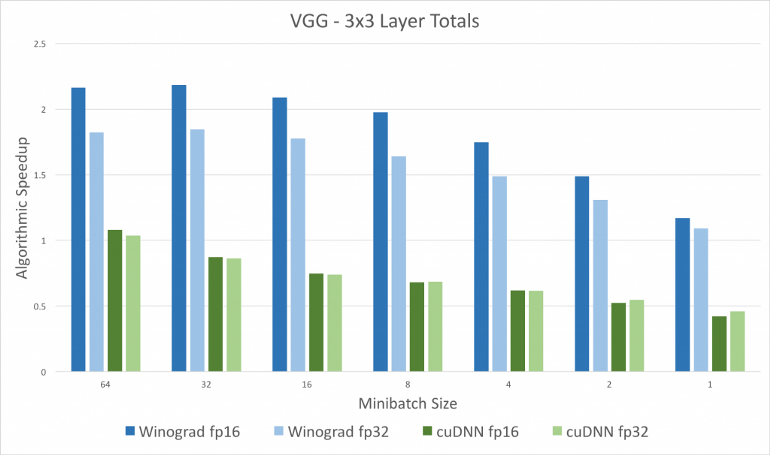 Winograd和CuDNN[/caption]
Winograd和CuDNN[/caption]
深度学习依赖于速度。更快的训练可以构建更大更复杂的网络。我们总是想要更快的网络来更快地检测自动驾驶汽车中的行人,并在资源受限的嵌入式设备和无限其他原因上启用网络。在CNN体系结构中,大部分时间都被卷积层所消耗。今天,我们将讨论Winograd算法,它可以将浮点乘法的数量减少2.25倍。
请参阅:算法文档详解
在我们开始讨论Winograd之前,我希望您了解卷积通常是如何在深度学习库中实现的。它们不是简单地以我们想象卷积的方式实现的。普通卷积的实现速度太慢,因为它们不能很好地利用CPU缓存和引用位置。为此,我们将卷积运算转换为矩阵乘法。让我们看看是怎么做的。
假设我们有大小为(4)的输入图像f和大小为(3)的过滤器g。
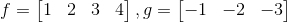
然后,利用im2col技术将输入图像转换为
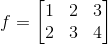
现在不要惊慌失措。我理解,这可能感觉我们增加了不必要的内存消耗,但现在我们可以使用BLAS库来执行矩阵乘法,如CuBLAS (GPU)或Intel MKL (CPU),它们对矩阵乘法进行了非常好的优化。
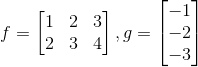
如果您想深入了解这一点,请查看
https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/content/making_faster.html
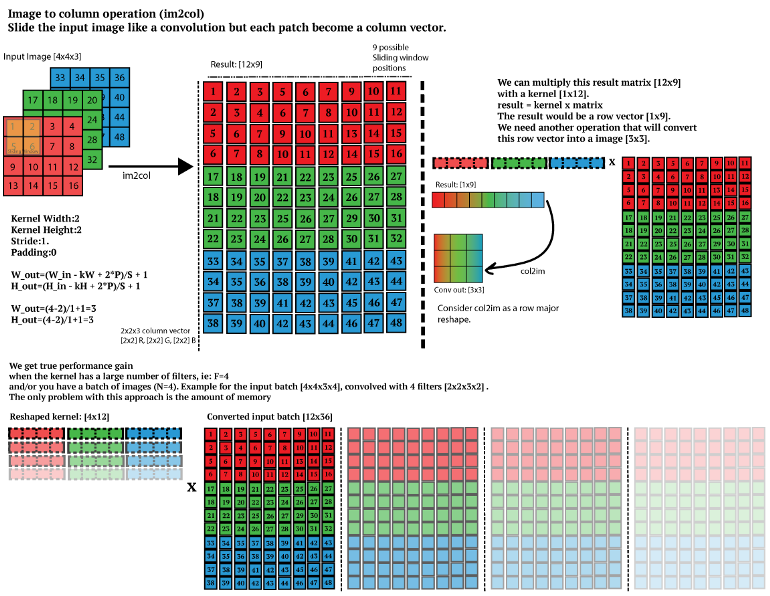
但我们是人类,总是朝着更好的方向发展。那么,我们如何进一步提高速度呢?现在,Winograd公司开始介入了。所以,我们不是做点积,而是用这个公式计算结果矩阵。

我们来概括一下。
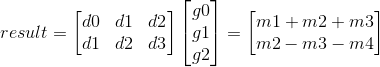
在该处:
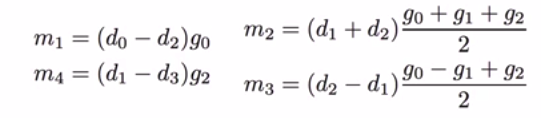
这样我们可以找到m1、m2、m3、m4的值。然后用它们来计算卷积,而不是矩阵的点积。这里我们可以观察到,(g0+g1+g2)/2和(g0-g1+g2)/2的值不需要在每次卷积操作中计算,因为过滤器保持不变。在训练过程中,我们可以在卷积之前计算一次,在推理过程中可以保存预先计算的结果。现在,我们需要
通过计算m1、m2、m3、m4、m4的计算值,在计算结果中进行4个加法运算和4个MUL运算,计算m1、m2、m3、m4的计算值。在做普通的点积时,我们要做6个MUL运算而不是4个。这使得计算上昂贵的MUL操作降低了1.5倍,这是非常重要的。
在上面的例子中,我用了F(4,3)也就是F(4)和g(3)得到了2个卷积。最小1 d算法F (m, r)嵌套与自身获得最小的2 d算法,F (m x m ,r x r)。如果我们试一试,F(4, 4)和g(3,3) 这将给我们4个卷积,我们将看到,Winograd方法正在4 * 4 = 16 MULs vs 2 * 2 * 9 = 36 MULs在正常卷积可以将MULs减少 2.25 倍,这太疯狂了! !你看!
我希望这篇文章能够帮助您了解在您使用的库后面使用了多少优化。我认为这能很好地解释Winograd是如何工作的。在未来的文章中,我们将进一步讨论嵌套最小过滤算法,其中我们将讨论如何针对不同的内核大小实现Winograd。
原文链接:https://medium.com/@dmangla3/understanding-winograd-fast-convolution-a75458744ff
 Winograd和CuDNN[/caption]
Winograd和CuDNN[/caption]深度学习依赖于速度。更快的训练可以构建更大更复杂的网络。我们总是想要更快的网络来更快地检测自动驾驶汽车中的行人,并在资源受限的嵌入式设备和无限其他原因上启用网络。在CNN体系结构中,大部分时间都被卷积层所消耗。今天,我们将讨论Winograd算法,它可以将浮点乘法的数量减少2.25倍。
请参阅:算法文档详解
在我们开始讨论Winograd之前,我希望您了解卷积通常是如何在深度学习库中实现的。它们不是简单地以我们想象卷积的方式实现的。普通卷积的实现速度太慢,因为它们不能很好地利用CPU缓存和引用位置。为此,我们将卷积运算转换为矩阵乘法。让我们看看是怎么做的。
假设我们有大小为(4)的输入图像f和大小为(3)的过滤器g。
然后,利用im2col技术将输入图像转换为
现在不要惊慌失措。我理解,这可能感觉我们增加了不必要的内存消耗,但现在我们可以使用BLAS库来执行矩阵乘法,如CuBLAS (GPU)或Intel MKL (CPU),它们对矩阵乘法进行了非常好的优化。
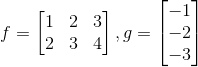
如果您想深入了解这一点,请查看
https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/content/making_faster.html

但我们是人类,总是朝着更好的方向发展。那么,我们如何进一步提高速度呢?现在,Winograd公司开始介入了。所以,我们不是做点积,而是用这个公式计算结果矩阵。

我们来概括一下。
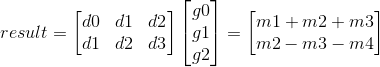
在该处:
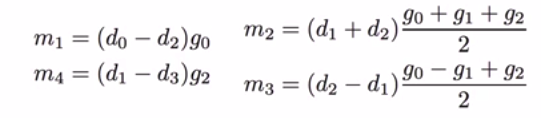
这样我们可以找到m1、m2、m3、m4的值。然后用它们来计算卷积,而不是矩阵的点积。这里我们可以观察到,(g0+g1+g2)/2和(g0-g1+g2)/2的值不需要在每次卷积操作中计算,因为过滤器保持不变。在训练过程中,我们可以在卷积之前计算一次,在推理过程中可以保存预先计算的结果。现在,我们需要
通过计算m1、m2、m3、m4、m4的计算值,在计算结果中进行4个加法运算和4个MUL运算,计算m1、m2、m3、m4的计算值。在做普通的点积时,我们要做6个MUL运算而不是4个。这使得计算上昂贵的MUL操作降低了1.5倍,这是非常重要的。
在上面的例子中,我用了F(4,3)也就是F(4)和g(3)得到了2个卷积。最小1 d算法F (m, r)嵌套与自身获得最小的2 d算法,F (m x m ,r x r)。如果我们试一试,F(4, 4)和g(3,3) 这将给我们4个卷积,我们将看到,Winograd方法正在4 * 4 = 16 MULs vs 2 * 2 * 9 = 36 MULs在正常卷积可以将MULs减少 2.25 倍,这太疯狂了! !你看!
结论
我希望这篇文章能够帮助您了解在您使用的库后面使用了多少优化。我认为这能很好地解释Winograd是如何工作的。在未来的文章中,我们将进一步讨论嵌套最小过滤算法,其中我们将讨论如何针对不同的内核大小实现Winograd。
原文链接:https://medium.com/@dmangla3/understanding-winograd-fast-convolution-a75458744ff

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























