自相关与偏自相关的简单介绍
2017年08月15日 由 yuxiangyu 发表
374396
0
自相关和偏自相关图在时间序列分析和预测中经常使用。
这些图生动的总结了一个时间序列的观察值与他之前的时间步的观察值之间的关系强度。初学者要理解时间序列预测中自相关和偏自相关之间的差别很困难。
在本教程中,您将发现如何使用Python来计算和绘制自相关图和偏自相关图。
完成本教程后,您将知道:
让我们开始吧。
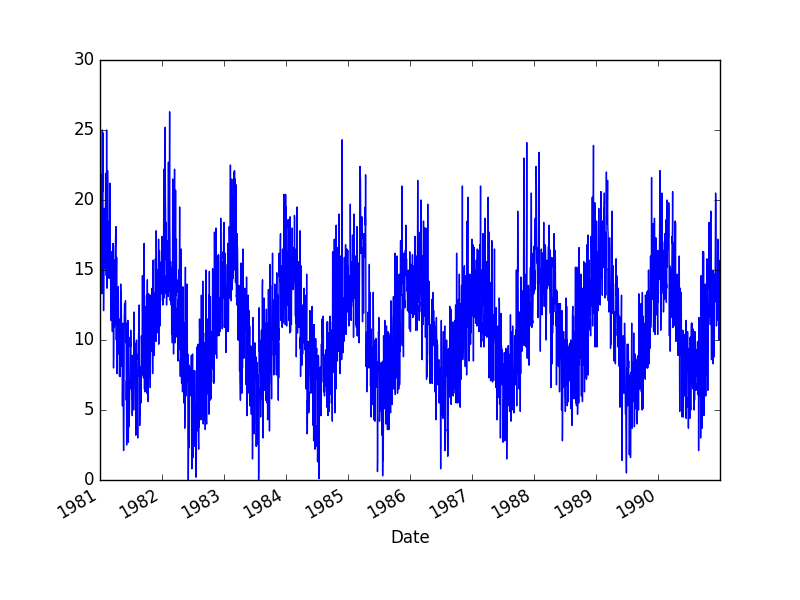
该数据集描述了澳大利亚墨尔本市10年(1981 - 1990年)的最低每日气温。
单位为摄氏度,观测值为3650次。数据来源于澳大利亚气象局。
点击这里了解更多信息并从Dara Market下载数据集。
下载数据集并将其放在您当前的工作目录中,文件名为“ daily-minimum-thermometer.csv ”。
注意:下载的文件包含一些问号(“?”)字符,必须先删除它然后才能使用数据集。在文本编辑器中打开文件,并删除“?”字符。同时删除文件中的任何页脚信息。
下面的示例将加载最低每日温度并绘制时间序列。
运行该示例将数据集加载为Pandas序列,并创建时间序列的折线图。
统计相关性总结了两个变量之间的关系强度。
我们可以假设每个变量的分布都符合高斯(钟形曲线)分布。如果是这样,我们可以使用皮尔逊相关系数(Pearson correlation coefficient)来总结变量之间的相关性。
皮尔逊相关系数是-1和1之间的数字分别描述负相关或正相关。值为零表示无相关。
我们可以使用以前的时间步长来计算时间序列观测的相关性。由于时间序列的相关性与之前的相同系列的值进行了计算,这被称为序列相关或自相关。
一个时间序列的自相关系数被称为自相关函数,或简称ACF。这个图被称为相关图或自相关图。
以下是利用statsmodels库中使用plot_acf()函数计算和绘制“每日最低气温”自相关图的一个例子。
运行示例创建一个2D平面图,显示沿x轴的延迟值以及y轴上的相关性(-1到1之间)。
置信区间被画成圆锥形。默认情况下,置信区间这被设置为95%,这表明,这段代码之外的相关值很可能是相关的,而不是统计上的意外。
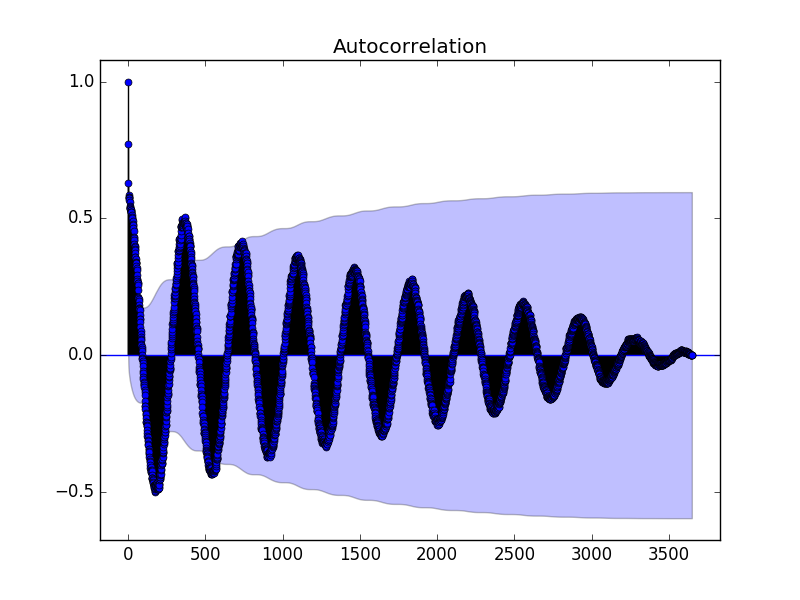
默认情况下,打印所有延迟值,这让显得图表有些杂乱。
我们可以将x轴上的延迟值限制为50,让图更容易看懂。
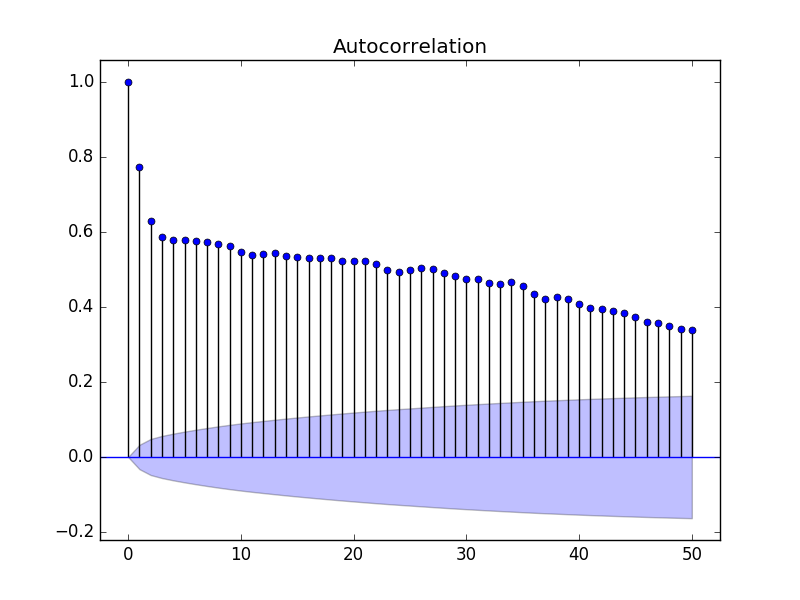
偏自相关是剔除干扰后时间序列观察与先前时间步长时间序列观察之间关系的总结。
- 第81页,第4.5.6节偏自相关,Introductory Time Series with R。
一项观察的自相关和在先验时间步上的观测包括直接相关和间接相关。这些间接相关是线性函数观察(这个观察在两个时间步长之间)的相关。
偏自相关函数试图移除这些间接相关。没有进入数学,这就是偏自相关的直觉。????
下面的示例使用statsmodels库中的plot_pacf()来计算和绘制最低每日温度数据集里的前50个滞后的偏自相关函数。
运行这个示例创建了前50个滞后的偏自相关的平面图。
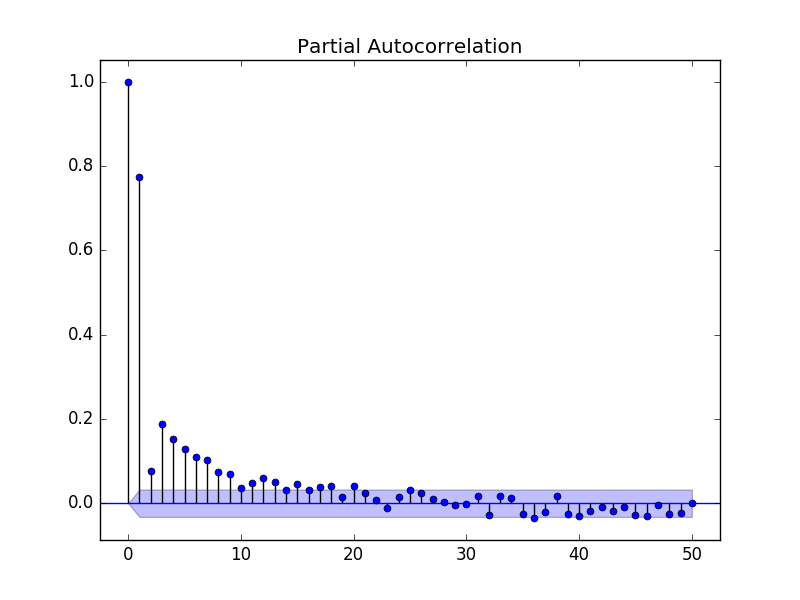
时间序列的自相关函数和偏自相关函数的平面图描述了完全不同的情形。
我们可以使用ACF和PACF的直觉来探索一些理想实验。
由具有滞后k的自回归(AR)过程生成的时间序列。
我们知道ACF描述了自相关在这个时间步的观察和前一个时间步的观察之间存在直接依赖信息和间接依赖信息。
这意味着,我们期望AR(k)时间序列里的ACF对k的滞后有很强的影响,并且这种关系的惯性将会延续到后来的滞后值中,在某种程度上随着效果的减弱而逐渐减弱。
我们知道,PACF仅描述观察与其滞后之间的直接关系。这表明除了k之外的滞后值没有相关性。
这正是ACF和PACF计划在AR(k)过程中的期望。
由k的滞后的移动平均(MA)过程产生的时间序列。
移动平均过程是先前预测中时间序列剩余误差的自回归模型。考虑移动平均模型的另一种方法是根据最近预测的错误来纠正对未来的预测。
我们预计ACF在MA(k)的过程中与最近的值显示出强相关性直到k的滞后,然后急剧下降到低或没有相关性。这就是生成该过程的方法。
我们预计绘图将显示出与滞后的密切关系,以及与滞后的相关性减弱。
这正是MA(k)过程的ACF和PACF图的预计。
在本教程中,您发现了如何使用Python计算时间序列数据的自相关和偏自相关图。
具体来说,您学到了:
这些图生动的总结了一个时间序列的观察值与他之前的时间步的观察值之间的关系强度。初学者要理解时间序列预测中自相关和偏自相关之间的差别很困难。
在本教程中,您将发现如何使用Python来计算和绘制自相关图和偏自相关图。
完成本教程后,您将知道:
- 如何绘制和检查时间序列的自相关函数。
- 如何绘制和检查时间序列的偏自相关函数。
- 时间序列分析中自相关函数和偏自相关函数之间的差异。
让我们开始吧。
每日最低气温数据集
该数据集描述了澳大利亚墨尔本市10年(1981 - 1990年)的最低每日气温。
单位为摄氏度,观测值为3650次。数据来源于澳大利亚气象局。
点击这里了解更多信息并从Dara Market下载数据集。
下载数据集并将其放在您当前的工作目录中,文件名为“ daily-minimum-thermometer.csv ”。
注意:下载的文件包含一些问号(“?”)字符,必须先删除它然后才能使用数据集。在文本编辑器中打开文件,并删除“?”字符。同时删除文件中的任何页脚信息。
下面的示例将加载最低每日温度并绘制时间序列。
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv('daily-minimum-temperatures.csv', header=0)
series.plot()
pyplot.show()
运行该示例将数据集加载为Pandas序列,并创建时间序列的折线图。

相关和自相关
统计相关性总结了两个变量之间的关系强度。
我们可以假设每个变量的分布都符合高斯(钟形曲线)分布。如果是这样,我们可以使用皮尔逊相关系数(Pearson correlation coefficient)来总结变量之间的相关性。
皮尔逊相关系数是-1和1之间的数字分别描述负相关或正相关。值为零表示无相关。
我们可以使用以前的时间步长来计算时间序列观测的相关性。由于时间序列的相关性与之前的相同系列的值进行了计算,这被称为序列相关或自相关。
一个时间序列的自相关系数被称为自相关函数,或简称ACF。这个图被称为相关图或自相关图。
以下是利用statsmodels库中使用plot_acf()函数计算和绘制“每日最低气温”自相关图的一个例子。
from pandas import Series
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
series = Series.from_csv('daily-minimum-temperatures.csv', header=0)
plot_acf(series)
pyplot.show()
运行示例创建一个2D平面图,显示沿x轴的延迟值以及y轴上的相关性(-1到1之间)。
置信区间被画成圆锥形。默认情况下,置信区间这被设置为95%,这表明,这段代码之外的相关值很可能是相关的,而不是统计上的意外。

默认情况下,打印所有延迟值,这让显得图表有些杂乱。
我们可以将x轴上的延迟值限制为50,让图更容易看懂。

偏自相关函数
偏自相关是剔除干扰后时间序列观察与先前时间步长时间序列观察之间关系的总结。
在滞后k处的偏自相关是在消除由于较短滞后条件导致的任何相关性的影响之后产生的相关性。
- 第81页,第4.5.6节偏自相关,Introductory Time Series with R。
一项观察的自相关和在先验时间步上的观测包括直接相关和间接相关。这些间接相关是线性函数观察(这个观察在两个时间步长之间)的相关。
偏自相关函数试图移除这些间接相关。没有进入数学,这就是偏自相关的直觉。????
下面的示例使用statsmodels库中的plot_pacf()来计算和绘制最低每日温度数据集里的前50个滞后的偏自相关函数。
from pandas import Series
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_pacf
series = Series.from_csv('daily-minimum-temperatures.csv', header=0)
plot_pacf(series, lags=50)
pyplot.show()
运行这个示例创建了前50个滞后的偏自相关的平面图。

ACF和PACF图的直觉
时间序列的自相关函数和偏自相关函数的平面图描述了完全不同的情形。
我们可以使用ACF和PACF的直觉来探索一些理想实验。
自回归直觉
由具有滞后k的自回归(AR)过程生成的时间序列。
我们知道ACF描述了自相关在这个时间步的观察和前一个时间步的观察之间存在直接依赖信息和间接依赖信息。
这意味着,我们期望AR(k)时间序列里的ACF对k的滞后有很强的影响,并且这种关系的惯性将会延续到后来的滞后值中,在某种程度上随着效果的减弱而逐渐减弱。
我们知道,PACF仅描述观察与其滞后之间的直接关系。这表明除了k之外的滞后值没有相关性。
这正是ACF和PACF计划在AR(k)过程中的期望。
移动平均线的直觉
由k的滞后的移动平均(MA)过程产生的时间序列。
移动平均过程是先前预测中时间序列剩余误差的自回归模型。考虑移动平均模型的另一种方法是根据最近预测的错误来纠正对未来的预测。
我们预计ACF在MA(k)的过程中与最近的值显示出强相关性直到k的滞后,然后急剧下降到低或没有相关性。这就是生成该过程的方法。
我们预计绘图将显示出与滞后的密切关系,以及与滞后的相关性减弱。
这正是MA(k)过程的ACF和PACF图的预计。
总结
在本教程中,您发现了如何使用Python计算时间序列数据的自相关和偏自相关图。
具体来说,您学到了:
- 如何计算并创建时间序列数据的自相关图。
- 如何计算和创建时间序列数据的偏自相关图。
- 解释ACF和PACF图的差异和直觉。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























