如何规避线性回归的陷阱(上)
2019年10月17日 由 sunlei 发表
801795
0
你总能通过数据科学新手快速适应神经网络的速度来发现他们。
神经网络很酷,可以做一些很棒的事情,对我们很多人(包括我自己)来说,这就是我们开始研究数据科学的原因。我的意思是,谁会进入数据科学领域去玩弄那些过时的线性回归模型呢?
然而,具有讽刺意味的是,除非你是在一个专业领域,如计算机视觉或自然语言处理,很多时候,简单的模型,如线性回归, 实际上比复杂的黑箱模型,比如神经网络和支持向量机,能更好地解决你的问题。
毕竟,线性回归模型是:
我听过一些资深的数据科学家,他们在尖端人工智能领域有着丰富的工作经验,正是因为这些原因,他们对线性回归大加赞赏。
然而,线性回归为数不多的缺点之一是它背后的严格假设。这些假设可能使线性回归模型不适合在一系列非常普遍的情况下使用。
幸运的是,线性回归已经存在了很长时间(确切地说,从19世纪初开始),以至于统计学家们早就找到了一种方法,在任何违背假设的情况发生时都能避开它们,同时仍然保留了与线性回归相关的许多优点。
然而,为了处理违反一个或多个线性回归假设的情况,首先需要能够识别何时发生这种违反。这意味着理解线性回归的核心假设。
线性回归的基础是五个关键的假设,所有这些都需要保持模型产生可靠的预测。具体地说:
如果你的数据恰好符合所有这些假设,那就太好了。去适应你的线性回归模型,然后下午就可以休息了。
然而,用滚石乐队的话来说,“你不可能总是得到你想要的”,如果你处理的是比简单的“玩具”数据集更高级的东西,那么至少有一个假设会被违反。
在这一点上,你有两个选择(a)生闷气,或(b)找到一个方法来绕过任何被打破的假设。
假设你选择选择B,那么这里有四种方法可以避免违反线性回归假设之一。
多重共线性是最容易识别和处理的问题之一。一般来说,如果两个输入变量的(绝对)相关系数大于0.8,那么很有可能存在多重共线性问题。
这样就很难解释模型的系数,也很难确定它们的统计意义,因为模型将两个不同名称下的一个变量,跨两个单独的输入变量的影响分割开来。
例如,考虑一个来自Kaggle的数据集,它给出10,000个个体的身高(以英寸为单位)、性别和体重(以磅为单位)。
使用Python的statsmodels包将模型拟合到这个数据集,得到以下拟合参数:
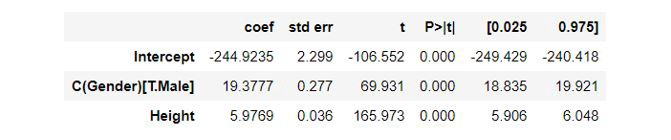
假设我们创建了一个新变量height_-cm,它以厘米为单位给出每个个体的高度(很明显,这与原始高度变量100%相关,因为以厘米为单位的高度=以英寸为单位的高度/2.54),然后重新调整我们的模型以包括这个新变量(除了原始变量之外)。
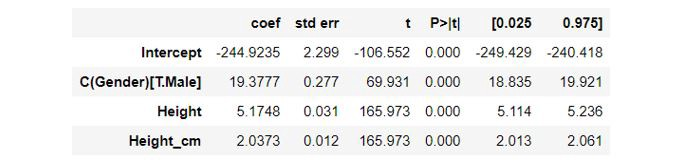
我们发现,第一个模型的高度系数现在被分割为height和Height_cm (可以验证为5.9769 = 5.1748 + 2.0373/2.54),这影响了两个变量的系数的可解释性。
多重共线性问题最简单的解决方案是从模型中删除一个高度相关的输入变量(与是哪一个无关)。
线性回归本质上是通过数据拟合一条(直线)最佳拟合线来实现的。在介绍统计学的课程中,他们通常会给出一些简单的“玩具”示例,这些示例都很好,但是如果您的数据与图表中的蓝点类似,会发生什么情况呢?
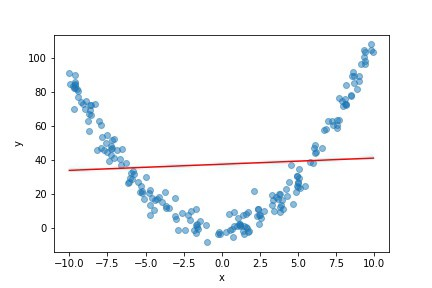
将直线回归线拟合到该数据(红线)将导致对所考虑范围中间的输入变量(x)值的输出变量(y)的预测过高,以及对范围任一极端的x值的预测过低。
为了捕捉这些数据的真实结构,我们真正需要做的是将多项式曲线拟合到我们的数据中,但这不能在线性回归的约束下完成,不是吗?
好吧,实际上,通过设计现有输入变量的函数(包括幂、对数和变量对的乘积)的新特性,可以使用线性回归来拟合数据,而不是直线。
例如,在上面的例子中,我们可以创建一个新的变量,z = x²然后符合我们的线性回归模型使用x和z作为输入变量。我们得到的模型将有以下形式:
它仍然是我们输入变量x和z的线性组合。但是,由于z只是x的函数,我们可以在二维中绘制拟合回归线,并得到如下结果:
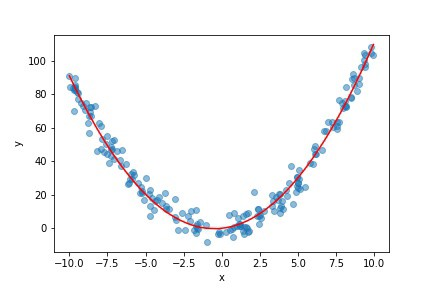
另外,这个例子说明了在尝试将模型放入数据之前先绘制数据图的重要性,因为通过可视化我们的数据,您可以了解哪些特性对工程师是有益的。
以上是今天更新的内容,是如何规避陷阱的两个方案,另外两个方案,我会继续更新。
原文链接:https://medium.com/analytics-vidhya/the-pitfalls-of-linear-regression-and-how-to-avoid-them-b93626e1a020
神经网络很酷,可以做一些很棒的事情,对我们很多人(包括我自己)来说,这就是我们开始研究数据科学的原因。我的意思是,谁会进入数据科学领域去玩弄那些过时的线性回归模型呢?
然而,具有讽刺意味的是,除非你是在一个专业领域,如计算机视觉或自然语言处理,很多时候,简单的模型,如线性回归, 实际上比复杂的黑箱模型,比如神经网络和支持向量机,能更好地解决你的问题。
毕竟,线性回归模型是:
- 快速训练和查询;
- 不易过度拟合和有效利用数据,因此可应用于相对较小的数据集;以及
- 很容易解释,即使对非技术背景的人也是如此。
我听过一些资深的数据科学家,他们在尖端人工智能领域有着丰富的工作经验,正是因为这些原因,他们对线性回归大加赞赏。
然而,线性回归为数不多的缺点之一是它背后的严格假设。这些假设可能使线性回归模型不适合在一系列非常普遍的情况下使用。
幸运的是,线性回归已经存在了很长时间(确切地说,从19世纪初开始),以至于统计学家们早就找到了一种方法,在任何违背假设的情况发生时都能避开它们,同时仍然保留了与线性回归相关的许多优点。
然而,为了处理违反一个或多个线性回归假设的情况,首先需要能够识别何时发生这种违反。这意味着理解线性回归的核心假设。
线性回归假设
线性回归的基础是五个关键的假设,所有这些都需要保持模型产生可靠的预测。具体地说:
- 线性:输入和输出变量之间的关系是线性的。我们表达我们的输出变量的期望值,Y,我们的输入变量的线性组合,X₁,…, Xₖ:E (Y) = b₀+ b₁X₁b + b₂X₂+…+ₖXₖ,₀b, b₁,…, bₖ表示拟合的模型参数。
- 无没有多重共线性:没有一个输入变量X₁,…, Xₖ,非常积极的还是消极的相互关联;
- 正态性:假设输出变量Y的观测值来自相同的正态分布。也就是说,Y~ iid N (m s²),其中m = E (Y)和s²表示Y的方差;
- Homoskedasticity:方差s²,输出的变量,Y,假定为常数,无论输入变量的值;以及
- 独立性:假设输出变量Y的观测值彼此独立。也就是说,在我们的输出变量中不存在自相关。
如果你的数据恰好符合所有这些假设,那就太好了。去适应你的线性回归模型,然后下午就可以休息了。
然而,用滚石乐队的话来说,“你不可能总是得到你想要的”,如果你处理的是比简单的“玩具”数据集更高级的东西,那么至少有一个假设会被违反。
在这一点上,你有两个选择(a)生闷气,或(b)找到一个方法来绕过任何被打破的假设。
假设你选择选择B,那么这里有四种方法可以避免违反线性回归假设之一。
解决方案1:移除输入变量以处理多重共线性
多重共线性是最容易识别和处理的问题之一。一般来说,如果两个输入变量的(绝对)相关系数大于0.8,那么很有可能存在多重共线性问题。
这样就很难解释模型的系数,也很难确定它们的统计意义,因为模型将两个不同名称下的一个变量,跨两个单独的输入变量的影响分割开来。
例如,考虑一个来自Kaggle的数据集,它给出10,000个个体的身高(以英寸为单位)、性别和体重(以磅为单位)。
使用Python的statsmodels包将模型拟合到这个数据集,得到以下拟合参数:
import pandas as pd
import statsmodels.formula.api as smf
# Load data
multi_data = pd.read_csv('weight-height.csv')
# Fit linear regression model to data
multi_model = smf.ols(formula='Weight ~ Height + C(Gender)', data=multi_data).fit()
# Print summary statistics
multi_model.summary()

假设我们创建了一个新变量height_-cm,它以厘米为单位给出每个个体的高度(很明显,这与原始高度变量100%相关,因为以厘米为单位的高度=以英寸为单位的高度/2.54),然后重新调整我们的模型以包括这个新变量(除了原始变量之外)。
multi_model2 = smf.ols(formula='Weight ~ Height + C(Gender) + Height_cm', data=multi_data).fit()
multi_model2.summary()

我们发现,第一个模型的高度系数现在被分割为height和Height_cm (可以验证为5.9769 = 5.1748 + 2.0373/2.54),这影响了两个变量的系数的可解释性。
多重共线性问题最简单的解决方案是从模型中删除一个高度相关的输入变量(与是哪一个无关)。
解决方案2:利用特征工程处理非线性问题
线性回归本质上是通过数据拟合一条(直线)最佳拟合线来实现的。在介绍统计学的课程中,他们通常会给出一些简单的“玩具”示例,这些示例都很好,但是如果您的数据与图表中的蓝点类似,会发生什么情况呢?
import numpy as np
import matplotlib.pyplot as plt
# Create dataset
np.random.seed(1)
x = np.random.uniform(-10, 10, 200)
y = x + x**2 + np.random.normal(0, 5, 200)
nl_data = pd.DataFrame({'X':x, 'Y':y})
# Fit linear regression to data
nl_model = smf.ols(formula='Y ~ X', data=nl_data).fit()
# Plot data and regression line
plt.scatter(x, y, alpha=0.5)
plt.xlabel('x')
plt.ylabel('y')
plt.plot(nl_data['X'], nl_model.predict(nl_data['X']), color = 'red')
plt.show()

将直线回归线拟合到该数据(红线)将导致对所考虑范围中间的输入变量(x)值的输出变量(y)的预测过高,以及对范围任一极端的x值的预测过低。
为了捕捉这些数据的真实结构,我们真正需要做的是将多项式曲线拟合到我们的数据中,但这不能在线性回归的约束下完成,不是吗?
好吧,实际上,通过设计现有输入变量的函数(包括幂、对数和变量对的乘积)的新特性,可以使用线性回归来拟合数据,而不是直线。
例如,在上面的例子中,我们可以创建一个新的变量,z = x²然后符合我们的线性回归模型使用x和z作为输入变量。我们得到的模型将有以下形式:
E(Y) = b₀+ b₁x + b₂z = b₀+ b₁x + b2x²
它仍然是我们输入变量x和z的线性组合。但是,由于z只是x的函数,我们可以在二维中绘制拟合回归线,并得到如下结果:
# Create engineered variable
nl_data.loc[:, 'X2'] = nl_data['X'].apply(lambda x: x**2)
# Refit model to data, including the new variable
nl_model2 = smf.ols(formula='Y ~ X + X2',
data=nl_data).fit()plt.scatter(x, y, alpha=0.5)
# Plot the data and the new regression line
plt.xlabel('x')
plt.ylabel('y')
plt.plot(nl_data['X'], nl_model2.predict(nl_data[['X', 'X2']]), color = 'red')
plt.show()

另外,这个例子说明了在尝试将模型放入数据之前先绘制数据图的重要性,因为通过可视化我们的数据,您可以了解哪些特性对工程师是有益的。
以上是今天更新的内容,是如何规避陷阱的两个方案,另外两个方案,我会继续更新。
原文链接:https://medium.com/analytics-vidhya/the-pitfalls-of-linear-regression-and-how-to-avoid-them-b93626e1a020

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
如何规避线性回归的陷阱(下)
热门企业
热门职位
写评论取消
回复取消






























