如何规避线性回归的陷阱(下)
2019年10月19日 由 sunlei 发表
893103
0
在上一部分中,我们学习了线性回归的概念和规避线性回归陷阱的前两个解决方案,今天我们继续学习剩余的两个方案。
前文回顾:如何规避线性回归的陷阱(上)
线性回归假设输出变量来自正态分布。也就是说,它是对称的,连续的,并且定义在整个数轴上。
实际上,违反后两个特征并不是什么大事。例如,在上面给出的身高与体重的例子中,尽管人类的体重通常只适合一个相对狭窄的范围,不能为负,但我们仍然可以对数据进行线性回归,而不必太在意。
然而,如果我们的数据是倾斜的,那么如果我们不纠正它,那就可能导致其他违反我们的线性回归假设的行为。
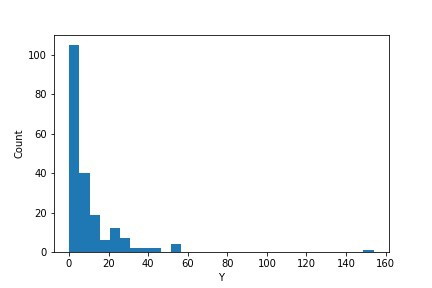
例如,考虑一个输出变量Y值为正偏态的数据集(gamma_data),如下图所示:
在不转换输出变量的情况下,将线性回归模型拟合到此数据集,然后根据输出变量的拟合值绘制残差,得到以下残差图:
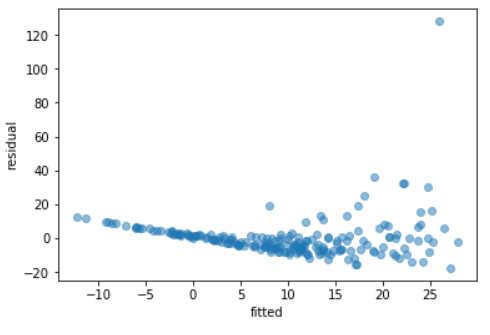
这个散点图上的点从左到右的扩散增加,这是异方差性的明显标志(即违反了同方差性假设)。
为了解决这个问题,我们可以在拟合模型之前转换输出变量,使其对称,例如,取其对数或平方根,如下所示:
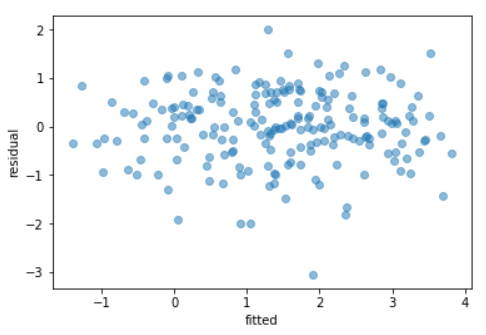
这个模型的残差现在显示出恒定的扩展,表明同质性。
或者,我们可以拟合专门为非正态数据设计的模型,,例如一个广义线性模型(GLM)。我在我的曾经的一篇文章中详细讨论了GLMs。
对于正偏态数据,gamma GLM通常是最佳选择。
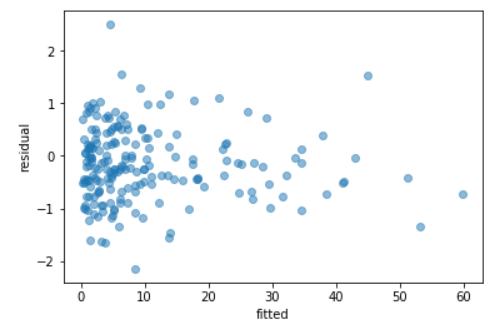
将gamma GLM与我们的数据进行日志连接,也解决了之前发现的异方差问题。
如果您正在处理定期收集的数据,即时间序列数据(例如,天气或金融数据),那么您的数据很可能是自相关的。自相关意味着了解输出变量的一个观察值可以为您提供前一个或下一个观察值的指示。
例如,在天气数据的背景下,如果你知道你所在城市今天的最高温度,那么你就会大致知道同一地点明天的最高温度(因为温度通常每天变化不大)。
检测数据中是否存在自相关的最简单方法是根据时间绘制输出变量。
以来自Kaggle的标准普尔500数据集为例。如果我们只关注一只股票(股票交易代码为“AAL”),并在数据集的持续时间内绘制收盘价:
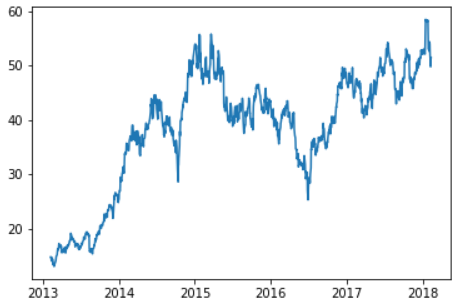
从图中我们可以清楚地看到,数据中存在自相关,这是标准的线性回归模型所不能处理的。
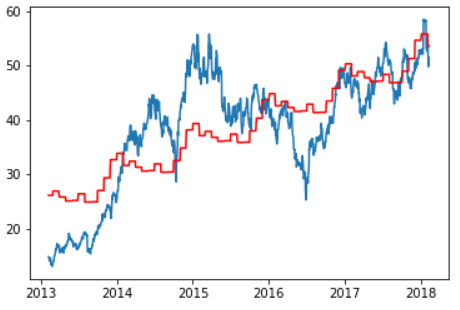
如果我们尝试用线性回归模型来拟合这些数据,使用年和月作为我们的输入变量,我们将得到如下所示的红线,这条红线对我们的数据的拟合不太理想:
为了在这个数据集中实现自相关,我们需要使用一个专门为处理时间序列而设计的模型,比如ARIMA模型。
给定时间t, Y(t)时刻的输出变量,ARIMA(p, d, q)模型首先取输出变量d连续几次的连续观测值之间的差,生成一个转换后的输出变量Y(t)。这样做是为了从数据中删除任何长期趋势,例如上图中显示的增长趋势。
一旦我们取了数据的d差,然后我们将得到的转换输出变量建模为y(t)的p立即先验观测值和q立即先验模型残值(即y(t)的实际值和预测值之间的差)的线性组合。
关于如何为参数p、d和q设置合适的值,有很多理论,这超出了本文的讨论范围。
为了这个例子,我们假设d=1,p=5和q=0。也就是说,在差分一次之后,为了考虑到我们数据中的总体增长趋势,可以将差分的输出值建模为前五个(差分的)输出值的线性组合。
此模型可以使用python statsmodels包中的tsa.arima函数进行拟合,并生成以下拟合模型:
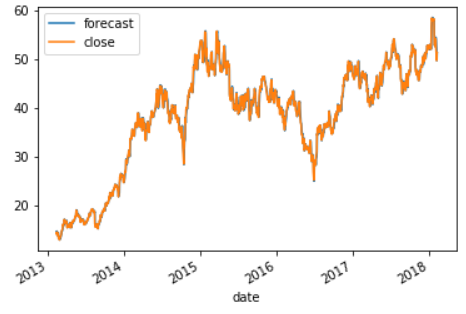
这个模型非常好地跟踪了我们的数据,由于预测线和实际线的跟踪非常紧密,几乎不可能区分两者。
另外,应该注意到,这种强大的性能部分是由于我们在用于拟合数据的样本中进行预测,而这种性能不太可能在样本外继续下去。
Occam剃刀原理指出,如果“对某一事件存在两种解释,通常需要最少猜测的解释是正确的”。
在数据科学的背景下,这意味着模型越复杂,解释数据的可能性就越小,或者在实际中,如果你试图对数据集建模,那么首先从最简单的模型开始,只有在简单的模型被证明不合适时,才考虑更复杂的模型。
对于回归问题,通常最简单的模型是线性回归模型。然而,在许多情况下,违反一个或多个严格的线性回归假设会使使用此模型不合适。
在本文中,我们为线性回归假设提供了一些解决方案,这些假设允许您继续使用这种高度通用且易于理解的模型(或相关模型,如glms或时间序列模型),然后再继续使用资源匮乏的黑盒技术,如神经网络。
线性回归模型可能不是很酷,但它们有可靠的跟踪记录,作为数据科学家,这才是真正重要的。
原文链接:https://medium.com/analytics-vidhya/the-pitfalls-of-linear-regression-and-how-to-avoid-them-b93626e1a020
前文回顾:如何规避线性回归的陷阱(上)
解决方案3:使用变量变换或广义线性模型来处理非正态性和异方差性
线性回归假设输出变量来自正态分布。也就是说,它是对称的,连续的,并且定义在整个数轴上。
实际上,违反后两个特征并不是什么大事。例如,在上面给出的身高与体重的例子中,尽管人类的体重通常只适合一个相对狭窄的范围,不能为负,但我们仍然可以对数据进行线性回归,而不必太在意。
然而,如果我们的数据是倾斜的,那么如果我们不纠正它,那就可能导致其他违反我们的线性回归假设的行为。
例如,考虑一个输出变量Y值为正偏态的数据集(gamma_data),如下图所示:
# Create gamma dataset
np.random.seed(1)
x1 = np.random.uniform(-1, 1, 200)
x2 = np.random.uniform(-1, 1, 200)
mu = np.exp(1 + x1 + 2*x2 + np.random.randn())
y = np.random.gamma(shape = 2, scale = mu/2, size = 200)
gamma_data = pd.DataFrame({'X1':x1, 'X2':x2, 'Y':y})
# Plot data
plt.hist(gamma_data['Y'], bins=30)
plt.ylabel('Count')
plt.xlabel('Y')
plt.show()

在不转换输出变量的情况下,将线性回归模型拟合到此数据集,然后根据输出变量的拟合值绘制残差,得到以下残差图:
# Fit linear regression
non_norm_model = smf.ols(formula='Y ~ X1 + X2',
data=gamma_data).fit()
# Calculate residuals
resid = gamma_data['Y'] - non_norm_model.predict(gamma_data[['X1', 'X2']])
# Plot residuals
plt.scatter(non_norm_model.predict(gamma_data[['X1', 'X2']]), resid, alpha=0.5)
plt.xlabel('fitted')
plt.ylabel('residual')
plt.show()

这个散点图上的点从左到右的扩散增加,这是异方差性的明显标志(即违反了同方差性假设)。
为了解决这个问题,我们可以在拟合模型之前转换输出变量,使其对称,例如,取其对数或平方根,如下所示:
# Transform Y by taking the log of it
gamma_data.loc[:, 'log_y'] = gamma_data['Y'].apply(lambda x:
np.log(x))
# Refit linear regression to transformed data
non_norm_model2 = smf.ols(formula='log_y ~ X1 + X2',
data=gamma_data).fit()
# Calculate residuals
resid = gamma_data['log_y'] -
non_norm_model2.predict(gamma_data[['X1', 'X2']])
# Plot residuals
plt.scatter(non_norm_model2.predict(gamma_data[['X1', 'X2']]), resid, alpha=0.5)
plt.xlabel('fitted')
plt.ylabel('residual')

这个模型的残差现在显示出恒定的扩展,表明同质性。
或者,我们可以拟合专门为非正态数据设计的模型,,例如一个广义线性模型(GLM)。我在我的曾经的一篇文章中详细讨论了GLMs。
对于正偏态数据,gamma GLM通常是最佳选择。
# Fit GLM to data
gamma_model = sm.GLM(gamma_data['Y'],
sm.add_constant(gamma_data[['X1', 'X2']]),
family=sm.families.Gamma(sm.genmod.families.links.log)).fit()
# Calculate residuals
resid = gamma_model.resid_deviance
# Plot residuals
plt.scatter(gamma_model.predict(sm.add_constant(gamma_data[['X1', 'X2']]),), resid, alpha=0.5)
plt.xlabel('fitted')
plt.ylabel('residual')
plt.show()

将gamma GLM与我们的数据进行日志连接,也解决了之前发现的异方差问题。
解决方案4:使用时间序列模型处理自相关
如果您正在处理定期收集的数据,即时间序列数据(例如,天气或金融数据),那么您的数据很可能是自相关的。自相关意味着了解输出变量的一个观察值可以为您提供前一个或下一个观察值的指示。
例如,在天气数据的背景下,如果你知道你所在城市今天的最高温度,那么你就会大致知道同一地点明天的最高温度(因为温度通常每天变化不大)。
检测数据中是否存在自相关的最简单方法是根据时间绘制输出变量。
以来自Kaggle的标准普尔500数据集为例。如果我们只关注一只股票(股票交易代码为“AAL”),并在数据集的持续时间内绘制收盘价:
# Read in dataset
sandp_data = pd.read_csv('all_stocks_5yr.csv')
# Only keep data for AAL
sandp_data = sandp_data[sandp_data['Name'] == 'AAL']
# Transform date to datetime format
sandp_data['date'] = pd.to_datetime(sandp_data['date'])
# Sort data by date
sandp_data.sort_values(by = ['date'], inplace = True)
# Plot data
plt.plot(sandp_data['date'], sandp_data['close'])
plt.show()

从图中我们可以清楚地看到,数据中存在自相关,这是标准的线性回归模型所不能处理的。
如果我们尝试用线性回归模型来拟合这些数据,使用年和月作为我们的输入变量,我们将得到如下所示的红线,这条红线对我们的数据的拟合不太理想:
# Create year and month variables
sandp_data['Year'] = sandp_data['date'].map(lambda x: x.year)
sandp_data['Month'] = sandp_data['date'].map(lambda x: x.month)
# Fit linear regression to data
sandp_model = smf.ols(formula='close ~ Year + C(Month)',
data=sandp_data).fit()# Plot data with regression line overlay
plt.plot(sandp_data['date'], sandp_data['close'])
plt.plot(sandp_data['date'], sandp_model.predict(sandp_data[['Year', 'Month']]), color = 'red')
plt.show()

为了在这个数据集中实现自相关,我们需要使用一个专门为处理时间序列而设计的模型,比如ARIMA模型。
给定时间t, Y(t)时刻的输出变量,ARIMA(p, d, q)模型首先取输出变量d连续几次的连续观测值之间的差,生成一个转换后的输出变量Y(t)。这样做是为了从数据中删除任何长期趋势,例如上图中显示的增长趋势。
例如,如果d=1,y(t)=y(t)-y(t-1),如果d=2,y(t)=z(t)-z(t-1),其中z(t)=y(t)-y(t-1),依此类推。
一旦我们取了数据的d差,然后我们将得到的转换输出变量建模为y(t)的p立即先验观测值和q立即先验模型残值(即y(t)的实际值和预测值之间的差)的线性组合。
关于如何为参数p、d和q设置合适的值,有很多理论,这超出了本文的讨论范围。
为了这个例子,我们假设d=1,p=5和q=0。也就是说,在差分一次之后,为了考虑到我们数据中的总体增长趋势,可以将差分的输出值建模为前五个(差分的)输出值的线性组合。
此模型可以使用python statsmodels包中的tsa.arima函数进行拟合,并生成以下拟合模型:
# Index dataset by date
sandp_data2 = sandp_data.set_index('date')
# Fit ARIMA model to the data
ts_model = sm.tsa.ARIMA(sandp_data2['close'], (5, 1, 0)).fit()
# Plot actual vs fitted values
ts_model.plot_predict(dynamic=False)

这个模型非常好地跟踪了我们的数据,由于预测线和实际线的跟踪非常紧密,几乎不可能区分两者。
另外,应该注意到,这种强大的性能部分是由于我们在用于拟合数据的样本中进行预测,而这种性能不太可能在样本外继续下去。
Occam剃刀原理指出,如果“对某一事件存在两种解释,通常需要最少猜测的解释是正确的”。
在数据科学的背景下,这意味着模型越复杂,解释数据的可能性就越小,或者在实际中,如果你试图对数据集建模,那么首先从最简单的模型开始,只有在简单的模型被证明不合适时,才考虑更复杂的模型。
对于回归问题,通常最简单的模型是线性回归模型。然而,在许多情况下,违反一个或多个严格的线性回归假设会使使用此模型不合适。
在本文中,我们为线性回归假设提供了一些解决方案,这些假设允许您继续使用这种高度通用且易于理解的模型(或相关模型,如glms或时间序列模型),然后再继续使用资源匮乏的黑盒技术,如神经网络。
线性回归模型可能不是很酷,但它们有可靠的跟踪记录,作为数据科学家,这才是真正重要的。
原文链接:https://medium.com/analytics-vidhya/the-pitfalls-of-linear-regression-and-how-to-avoid-them-b93626e1a020

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
上一篇
如何规避线性回归的陷阱(上)
下一篇
Python可视化解析MCMC
热门企业
热门职位
写评论取消
回复取消






























