图卷积网络图深度学习(上)
2019年10月26日 由 sunlei 发表
343760
0
基于图的机器学习是一项困难的任务,因为图的结构非常复杂,而且信息量也很大。本文是关于如何利用图卷积网络(GCNs)对图进行深度学习的系列文章中的第一篇。GCNs是一种功能强大的神经网络,旨在直接处理图并利用图的结构信息。该系列文章包括:
1、图卷积网络的高级介绍
2、基于谱图卷积的半监督学习
在本文中,我将介绍GCNs,并使用编码示例说明信息如何通过GCN的隐藏层传播。我们将看到GCN如何聚合来自前一层的信息,以及这种机制如何生成图中节点的有用特性表示。
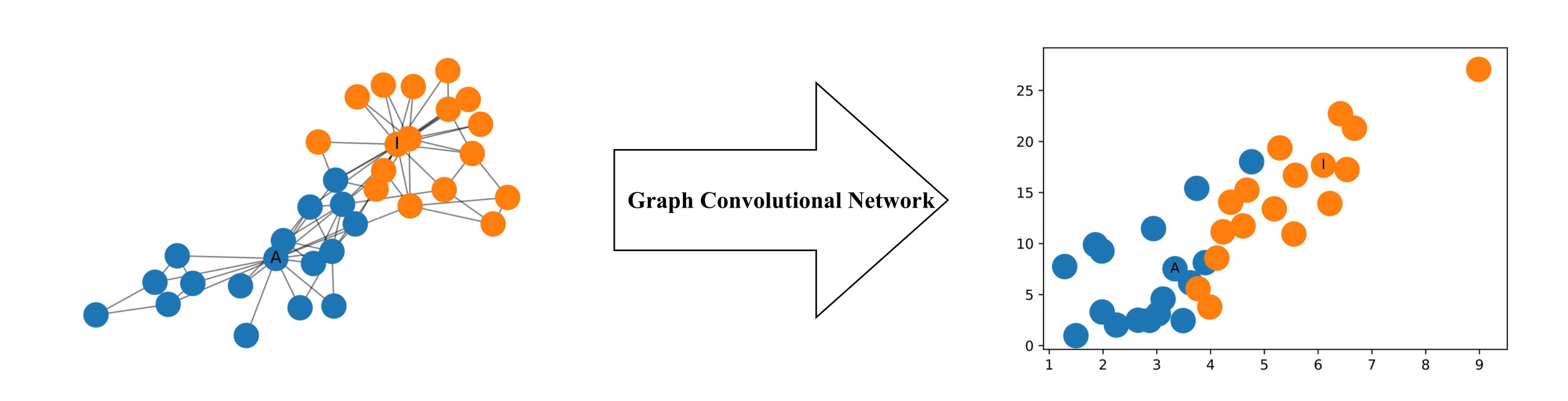
GCNs是一种非常强大的用于图形机器学习的神经网络体系结构。事实上,它们非常强大,即使是随机启动的2层GCN也可以生成网络中节点的有用特征表示。下图展示了由这样一个GCN生成的网络中每个节点的二维表示。请注意,即使没有任何训练,网络中节点的相对接近性也保留在二维表示中。
一个隐藏层的GCN因此可以写成Hⁱ = f(Hⁱ⁻¹, A)) 其中 H⁰ = X 和f是一个传播[1]。每一层Hⁱ对应于一个N×Fⁱ特性矩阵,其中每一行是一个节点的特征表示。在每一层,使用传播规则f将这些特征聚合起来形成下一层的特征。这样,在每一层上,特征变得越来越抽象。在这个框架中,GCN的变体只在传播规则f[1]的选择上有所不同。
最简单的传播规则之一是[1]:
f(Hⁱ, A) = σ(AHⁱWⁱ)
Wⁱ第i层的权重矩阵,σ是一个非线性激活函数,如ReLU函数。权重矩阵维度Fⁱ×Fⁱ⁺¹;换句话说,权重矩阵的第二维的大小决定了下一层的特征数。如果您熟悉卷积神经网络,那么这个操作类似于过滤操作,因为这些权重在图中的节点之间共享。
让我们在最简单的层次上研究传播规则。让
也就是说,f(X, A) = AX。这个传播规则可能太简单了,但是我们将在稍后添加缺少的部分。顺便提一下,AX现在相当于多层感知器的输入层。
作为一个简单的例子,我们将使用下图:
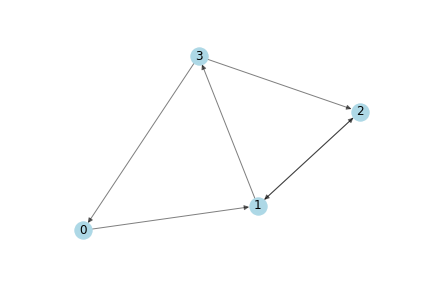
下面是它的numpy邻接矩阵表示。
接下来,我们需要功能!我们根据节点的索引为每个节点生成2个整数特征。这样便于以后手动确认矩阵计算。
好吧!我们现在有一个图,它的邻接矩阵A和一组输入特征X。让我们看看当我们应用传播规则时会发生什么:
发生了什么事?每个节点(每一行)的表示现在是其邻居特性的总和!换句话说,图卷积层将每个节点表示为其邻域的集合。我鼓励你自己检查一下计算结果。注意,在这种情况下,如果存在一条从v到n的边,则节点n是节点v的邻居。
你可能已经发现了问题:
节点的聚合表示不包括其自身的功能!该表示是邻居节点特征的聚合,因此只有具有自循环的节点才会在聚合中包含自己的特征。[1]
具有大角度的节点在其特征表示中将具有大值,而具有小角度的节点将具有小值。这可能导致梯度消失或爆炸[1,2],但对于通常用于训练此类网络且对每个输入特征的比例(或值的范围)敏感的随机梯度下降算法也是有问题的。
下面,我将分别讨论这些问题。
为了解决第一个问题,可以简单地向每个节点添加一个self-loop[1,2]。在实践中,这是通过在应用传播规则之前将恒等矩阵I添加到邻接矩阵A来实现的。
由于节点现在是其自身的邻居,因此在总结其邻居的特征时会包含该节点的自身特征!今天就先更新到这里,剩余的部分明天继续。
原文链接:https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780
1、图卷积网络的高级介绍
2、基于谱图卷积的半监督学习
在本文中,我将介绍GCNs,并使用编码示例说明信息如何通过GCN的隐藏层传播。我们将看到GCN如何聚合来自前一层的信息,以及这种机制如何生成图中节点的有用特性表示。
什么是图卷积网络?
GCNs是一种非常强大的用于图形机器学习的神经网络体系结构。事实上,它们非常强大,即使是随机启动的2层GCN也可以生成网络中节点的有用特征表示。下图展示了由这样一个GCN生成的网络中每个节点的二维表示。请注意,即使没有任何训练,网络中节点的相对接近性也保留在二维表示中。

- 更正式地说,图卷积网络(GCN)是一种对图进行操作的神经网络。给定一个图G = (V, E), GCN作为输入
- 一个输入特征矩阵N×F⁰特性矩阵,X,其中N是节点的数量和F⁰输入特征为每个节点的数量,和图结构的N×N矩阵表示,如[1]的邻接矩阵A[1]
一个隐藏层的GCN因此可以写成Hⁱ = f(Hⁱ⁻¹, A)) 其中 H⁰ = X 和f是一个传播[1]。每一层Hⁱ对应于一个N×Fⁱ特性矩阵,其中每一行是一个节点的特征表示。在每一层,使用传播规则f将这些特征聚合起来形成下一层的特征。这样,在每一层上,特征变得越来越抽象。在这个框架中,GCN的变体只在传播规则f[1]的选择上有所不同。
一个简单的传播规则
最简单的传播规则之一是[1]:
f(Hⁱ, A) = σ(AHⁱWⁱ)
Wⁱ第i层的权重矩阵,σ是一个非线性激活函数,如ReLU函数。权重矩阵维度Fⁱ×Fⁱ⁺¹;换句话说,权重矩阵的第二维的大小决定了下一层的特征数。如果您熟悉卷积神经网络,那么这个操作类似于过滤操作,因为这些权重在图中的节点之间共享。
简化
让我们在最简单的层次上研究传播规则。让
- i = 1, s.t. f是输入特征矩阵的函数,
- σ是恒等函数
- 选择权重t. AH⁰W⁰ =AXW⁰ = AX.
也就是说,f(X, A) = AX。这个传播规则可能太简单了,但是我们将在稍后添加缺少的部分。顺便提一下,AX现在相当于多层感知器的输入层。
一个简单的图形示例
作为一个简单的例子,我们将使用下图:

下面是它的numpy邻接矩阵表示。
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
接下来,我们需要功能!我们根据节点的索引为每个节点生成2个整数特征。这样便于以后手动确认矩阵计算。
In [3]: X = np.matrix([
[i, -i]
for i in range(A.shape[0])
], dtype=float)
XOut[3]: matrix([
[ 0., 0.],
[ 1., -1.],
[ 2., -2.],
[ 3., -3.]
])
应用传播规则
好吧!我们现在有一个图,它的邻接矩阵A和一组输入特征X。让我们看看当我们应用传播规则时会发生什么:
In [6]: A * X
Out[6]: matrix([
[ 1., -1.],
[ 5., -5.],
[ 1., -1.],
[ 2., -2.]]
发生了什么事?每个节点(每一行)的表示现在是其邻居特性的总和!换句话说,图卷积层将每个节点表示为其邻域的集合。我鼓励你自己检查一下计算结果。注意,在这种情况下,如果存在一条从v到n的边,则节点n是节点v的邻居。
哦!问题就在眼前!
你可能已经发现了问题:
节点的聚合表示不包括其自身的功能!该表示是邻居节点特征的聚合,因此只有具有自循环的节点才会在聚合中包含自己的特征。[1]
具有大角度的节点在其特征表示中将具有大值,而具有小角度的节点将具有小值。这可能导致梯度消失或爆炸[1,2],但对于通常用于训练此类网络且对每个输入特征的比例(或值的范围)敏感的随机梯度下降算法也是有问题的。
下面,我将分别讨论这些问题。
添加自循环
为了解决第一个问题,可以简单地向每个节点添加一个self-loop[1,2]。在实践中,这是通过在应用传播规则之前将恒等矩阵I添加到邻接矩阵A来实现的。
In [4]: I = np.matrix(np.eye(A.shape[0]))
I
Out[4]: matrix([
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]
])
In [8]: A_hat = A + I
A_hat * X
Out[8]: matrix([
[ 1., -1.],
[ 6., -6.],
[ 3., -3.],
[ 5., -5.]])
由于节点现在是其自身的邻居,因此在总结其邻居的特征时会包含该节点的自身特征!今天就先更新到这里,剩余的部分明天继续。
原文链接:https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
上一篇
Python可视化解析MCMC
下一篇
图卷积网络图深度学习(下)
热门企业
热门职位
写评论取消
回复取消






























