深度学习不只是“Import Tensorflow”(下)
2019年11月24日 由 sunlei 发表
495145
0
上一部分我们通过努力得到了一个不错的基本神经元,今天我们将会得到一个不同的线性模型!
前文回顾:深度学习不只是“Import Tensorflow”(上)
线性回归模型最小化了输入实际输出与模型预测输出之间的误差。类似地,理想的神经网络试图做到这一点。
神经元与线性回归模型的不同之处在于神经元可以接受几个加权的输入,其中输入的数量用字母i表示。
数学上是这样的:
换言之,任何神经元的输出vₖ仅仅是xᵢ×wᵢ的所有i值加上bₖ的总和。
但是想象一下我们有17个输入……用手把它们全部写出来不是很乏味吗?
这就是为什么我们将函数压缩为一个简单而优雅的方程:
为了澄清,下标ₖ表示节点的当前层,从输入层开始。
这样不是更好看吗?从视觉上看,我们的新节点是这样的:
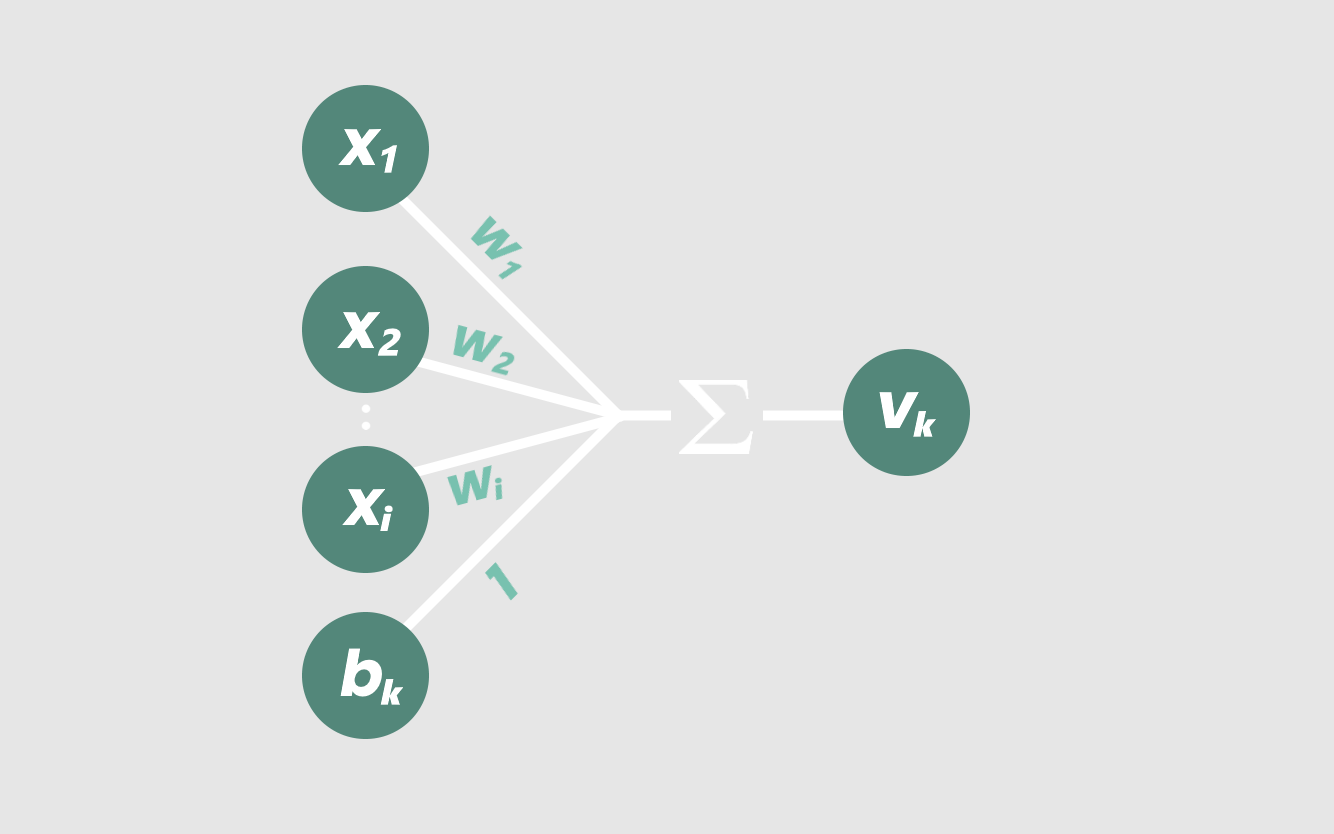
当我们增加输入的数量时,我们的方程开始在越来越高的维度上建模线性关系。例如,一个具有三个加权输入的节点
就会得到三维的等值线:平面。
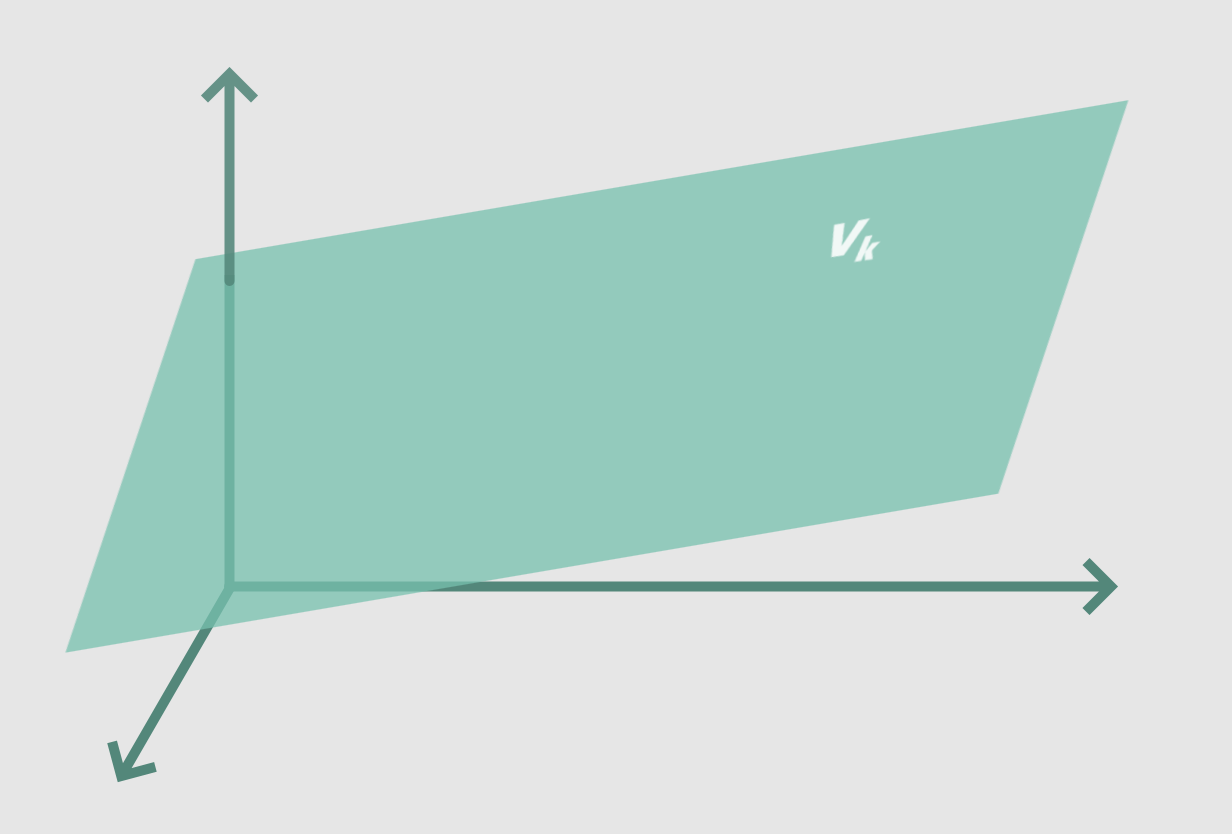
如果我们向节点添加更多的输入,我们将增加由节点方程建模的维度数。它最终将建立一个i维超平面的模型,这相当于i维空间中的一条直线。
(如果你不能想象,不要担心,因为我也不能)。
到目前为止,我们所概述的函数仅适用于神经网络一层中的单个节点。每个节点的输出vₖ,成为下一层中每个节点的输入。
然后这个过程在神经网络的每一层中的每一个节点上重复!我知道,在这样高维度的复杂度下,你的思维有点困难。不幸的是,至少目前我们只限于三维大脑。但那是另一个故事了。
记住,如果我们采用当前的分层神经网络,随机设置所有的权值和偏差,那么在输出节点处得到的权值函数仍然是直线的。
不管我们如何组合权重和和,我们总会得到一个线性模型……这就是目前为止数学的计算方法。
虽然建立线性关系模型可能很有趣,但这并不是非常有用。我们希望我们的神经网络能够解释复杂的非线性关系。
因此,我们将在每个节点上修改线性方程,为我们的网络增加一些非线性,我们称之为“激活函数”。
把它想象成一个“激活”我们的神经网络的函数,因为它的目的是使我们的网络从建模线性i维超平面到建模非线性i维函数。一个流行的激活函数是logistic曲线,也被称为sigmoid函数:
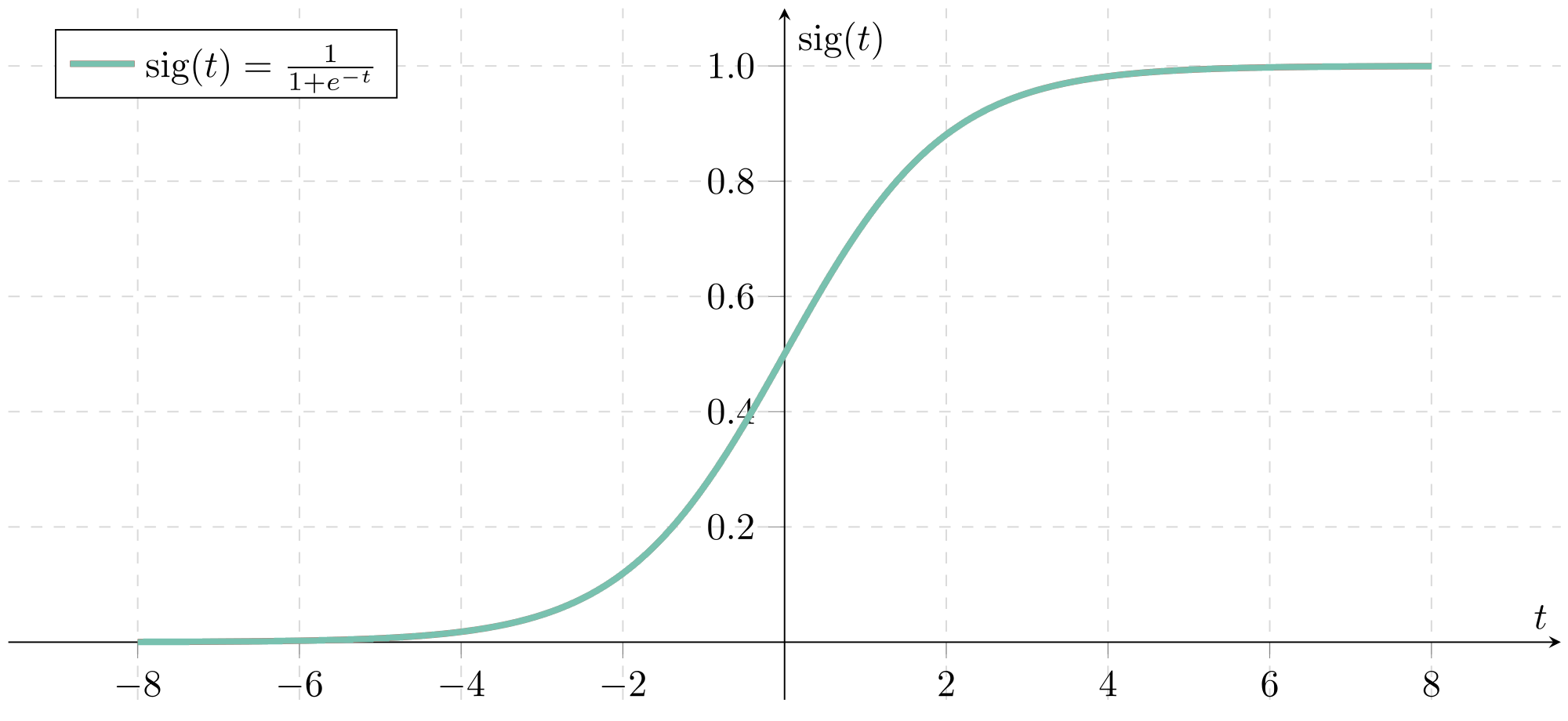
这个函数“压制”了我们的加权和,因此不管它们的值有多高或多低,它们最终总是在0和1之间。将我们在每个节点上的现有方程通过sigmoid函数后,我们修改后的方程为:
or
将此组件添加到我们的关系图中,现在我们有:
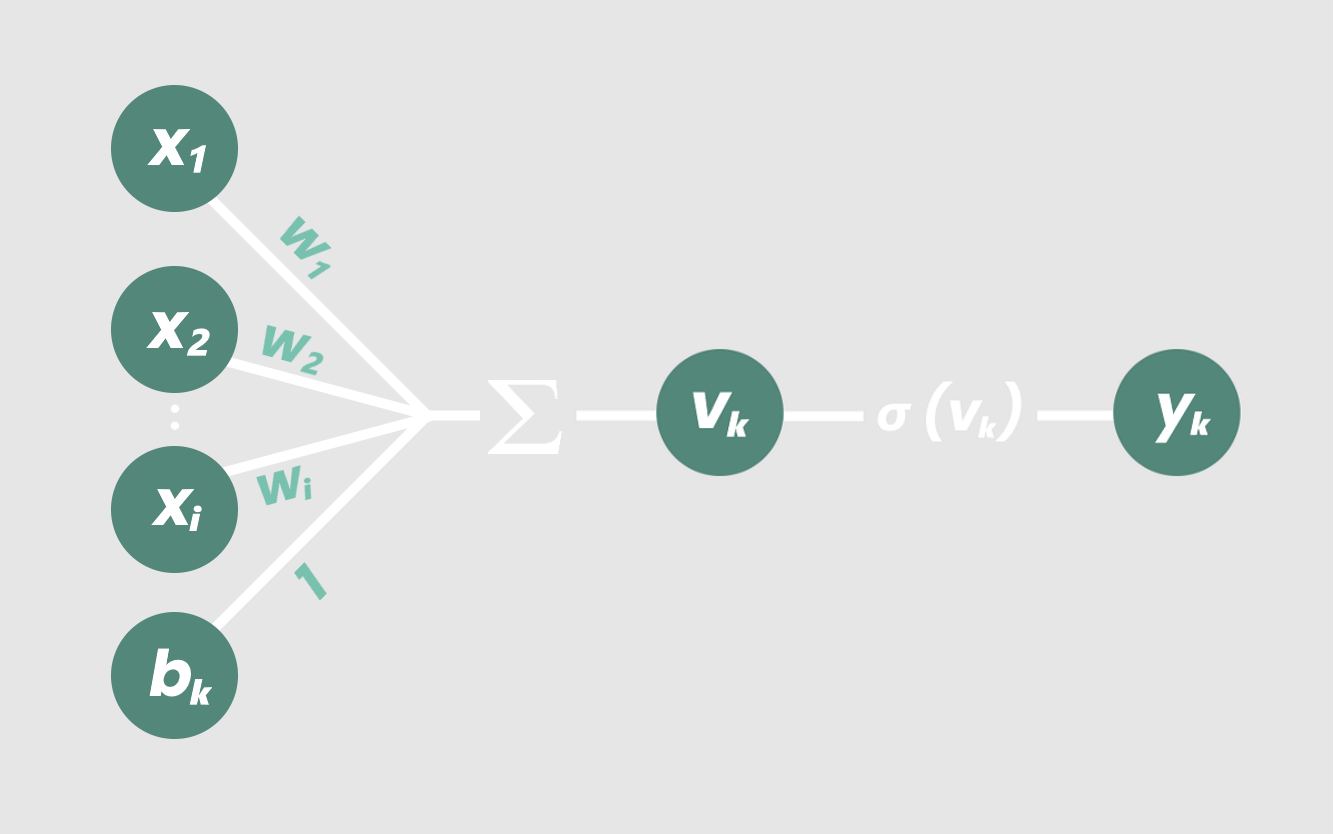
现在,我们的节点实际上已经完成了!
sigmoid函数允许我们的节点考虑多个输入之间的交互效果和非线性关系。当与网络中所有其他节点连接时,我们的神经网络获得了建模复杂非线性i维关系的能力。
一个神经网络模型之间的关系,只有三个输入可能最终会像这样:
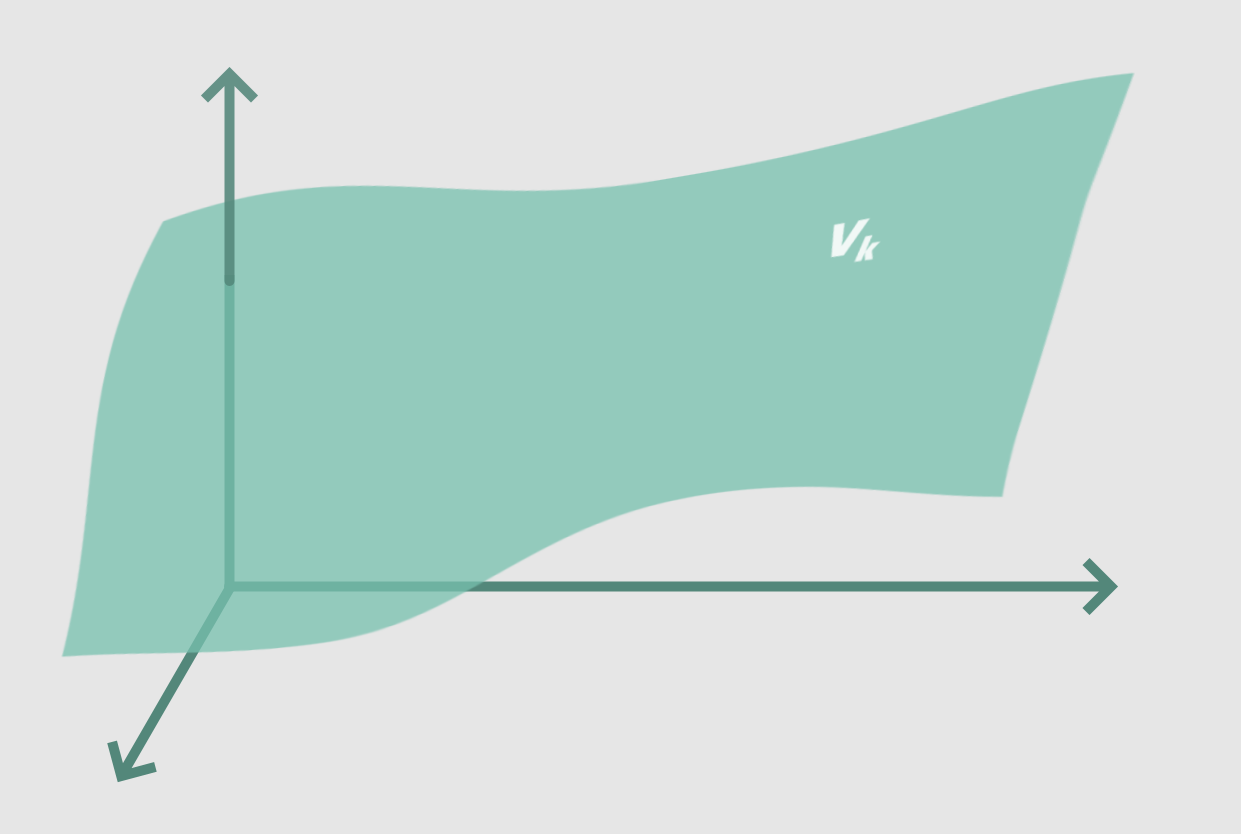
但是,像上面显示的非线性平面这样简单的东西,可以由人类来计算。我们真的不需要一个神经网络来模拟三维空间的功能。
但是当我们开始处理越来越多的变量并进入越来越高的维度时,神经网络变得非常有用。我的意思是,我们怎么会想出一个能精确映射上千个变量的模型呢?
答案是——我们没有。这就是神经网络的作用!
让我重申:
当加权输入被加在一起并在每个节点上通过一个激活函数时,神经网络获得了建模复杂非线性i维关系的能力。
这就是为什么神经网络如此有用。
由于我们可以修改每个节点的权值和偏差,因此我们的神经网络现在在理论上应该能够学习和建模任意数量变量之间的任何关系。
考虑到这一切,我们开始在每个节点上用随机的一组权重和偏差来训练我们的神经网络。
当我们向网络提供大量包含输入和正确输出的数据和训练示例时,网络尝试将输入映射到相应的输出。
输出层中最“活跃”的节点(换句话说,它返回的值比其他输出节点的加权和要高)是神经网络对给定输入集的“正确答案”的选择。
显然,由于我们从每个节点的随机权重和偏差开始,网络的预测从一开始就不准确。这就是我们需要训练网络的原因。
我们向网络展示我们的训练示例的正确答案,我们基本上告诉网络,看看它的预测与每次正确答案的接近程度。我们通过使用损失函数计算输出中的误差:
我们的目标是最小化误差以提高网络的准确性。将这个过程形象化的一个简单方法是将图形误差想象成一个向上开口的抛物线函数,其中底部的波谷代表最小的误差。
我们使用一种叫做梯度下降的方法来最小化我们的点在这个损失函数上的导数。这是一种有趣的说法,如果我们要画一条与点相切的直线,我们希望它的斜率尽可能小。
想想看,抛物线的切线斜率为0的唯一点是最底端的点,损失最小!
知道点对损失函数的导数是非常有用的因为它变得越小,误差就越小。
因此,梯度下降函数通过将神经网络的误差点向下移动到损失函数的局部最小值来帮助我们最小化损失。
在实践中,我们的损失函数不会是一个双变量抛物线,因为大多数神经网络不止有两个输入,因此也不止有两个变量。
相反,损失函数将类似于多维空间中的山和谷。因此,梯度下降函数通过最小化损失函数上的点的“梯度”或多变量导数来减少误差。
因此,与其在抛物线上降低我们的损失,不如把梯度下降的过程想象成把一个球滚下山,这个球代表了我们神经网络的误差量。
[caption id="attachment_47182" align="aligncenter" width="1200"]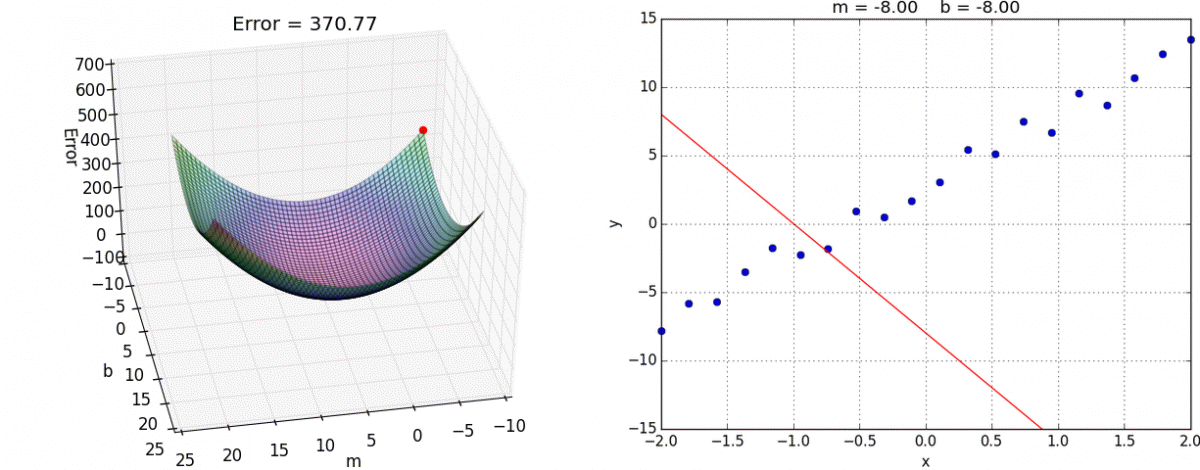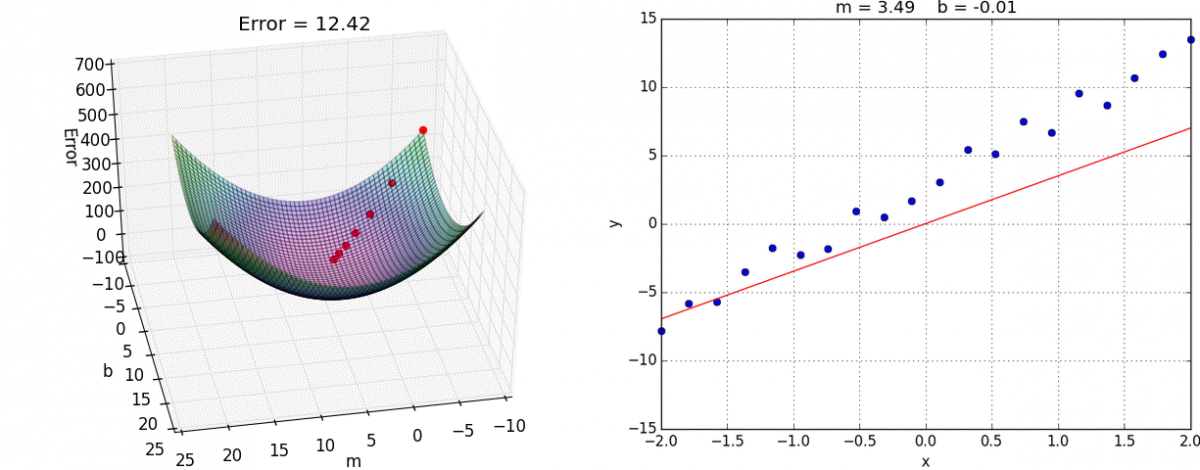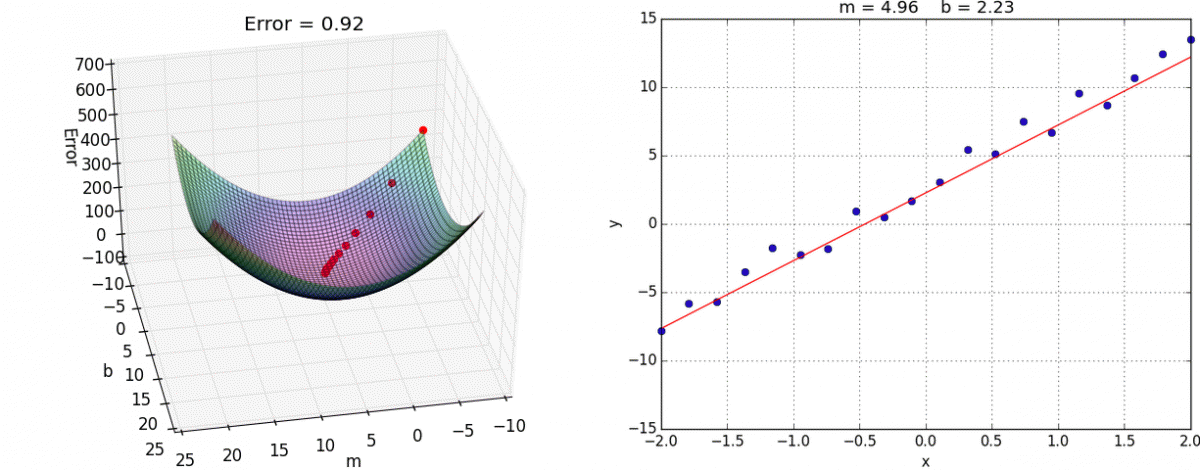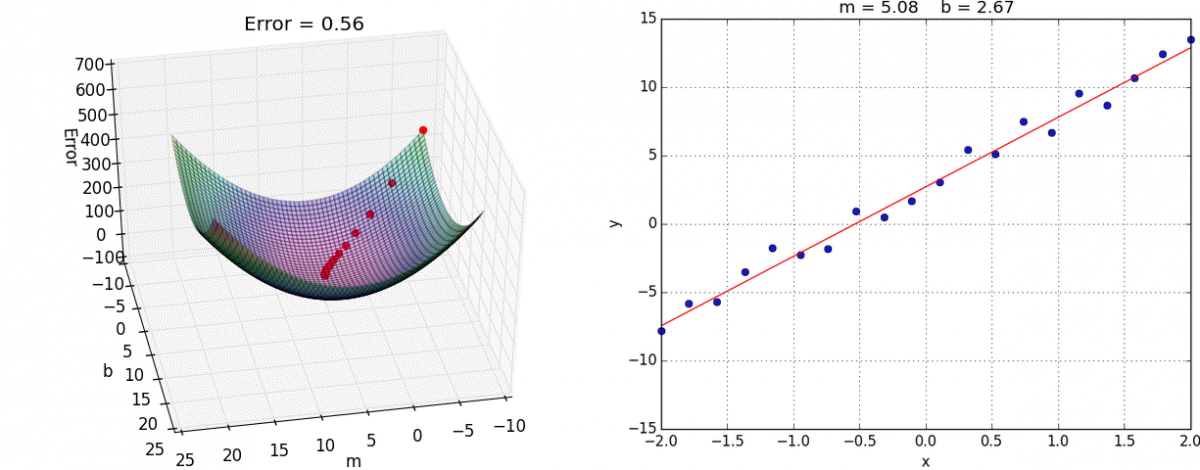 我们在这里使用线性回归模型来保持可视化的简单性。观察模型的准确性如何提高(右),因为它的点在损失函数(左)“滚下山”。[/caption]
我们在这里使用线性回归模型来保持可视化的简单性。观察模型的准确性如何提高(右),因为它的点在损失函数(左)“滚下山”。[/caption]
简而言之,梯度下降法使网络能够计算出给定一组输入时,它的输出是需要更大的正值还是负值,以便在进行预测时提高网络的整体准确性。
一旦通过损失函数计算出误差,网络中的权值和偏差就会被修正以使误差最小化。这是通过一种叫做反向传播的方法实现的:
其中W(k+1)表示新的权值,W(k)表示当前权值。
反向传播函数将错误从输出层向后传播到网络中的每一层。它本质上允许我们修改神经网络中节点之间的每一个权重的值,使一些节点变得比其他节点更“活跃”。
[caption id="attachment_47183" align="aligncenter" width="480"]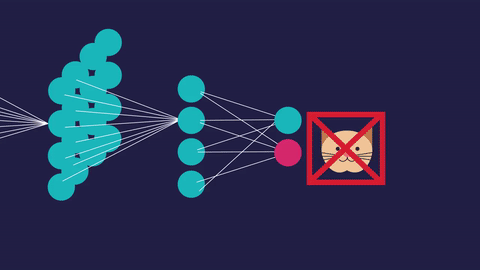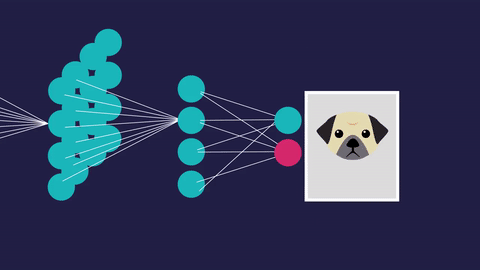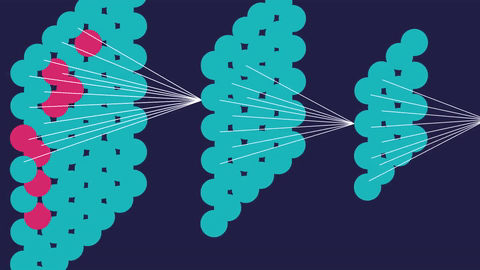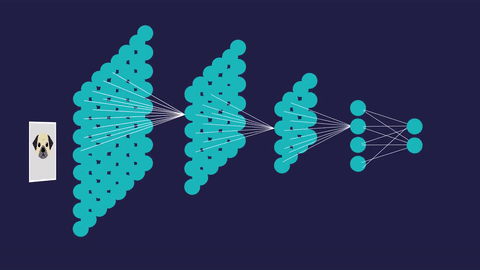 可视化反向传播。图像来源于虚构到事实。[/caption]
可视化反向传播。图像来源于虚构到事实。[/caption]
这些修改的目的是最小化神经网络的损失或误差。经过无数次的反复训练,损失最小化,我们的神经网络在工作中变得越来越精确,无论是识别手写数字还是推荐你下一个YouTube视频。
你绝对是个传奇。我没有耐心读完所有的东西(考虑到是我写的,这很有趣)。你真棒!
更重要的是,现在除了导入TensorFlow之外,您对神经网络如何工作有了更直观的理解。
我希望您学到了一些有价值的东西,我们下一篇文章再见!
前文回顾:深度学习不只是“Import Tensorflow”(上)
但是如果我们增加更多的投入呢?
线性回归模型最小化了输入实际输出与模型预测输出之间的误差。类似地,理想的神经网络试图做到这一点。
神经元与线性回归模型的不同之处在于神经元可以接受几个加权的输入,其中输入的数量用字母i表示。
数学上是这样的:
vₖ = x₁ × w₁ + x₂ × w₂ . . . + xᵢ × wᵢ + bₖ.
换言之,任何神经元的输出vₖ仅仅是xᵢ×wᵢ的所有i值加上bₖ的总和。
但是想象一下我们有17个输入……用手把它们全部写出来不是很乏味吗?
这就是为什么我们将函数压缩为一个简单而优雅的方程:
vₖ = ∑ ( xᵢ × wᵢ ) + bₖ
为了澄清,下标ₖ表示节点的当前层,从输入层开始。
这样不是更好看吗?从视觉上看,我们的新节点是这样的:

当我们增加输入的数量时,我们的方程开始在越来越高的维度上建模线性关系。例如,一个具有三个加权输入的节点
vₖ = x₁ × w₁ + x₂ × w₂ + x₃ × w₃ + b₁
就会得到三维的等值线:平面。

如果我们向节点添加更多的输入,我们将增加由节点方程建模的维度数。它最终将建立一个i维超平面的模型,这相当于i维空间中的一条直线。
(如果你不能想象,不要担心,因为我也不能)。
到目前为止,我们所概述的函数仅适用于神经网络一层中的单个节点。每个节点的输出vₖ,成为下一层中每个节点的输入。
然后这个过程在神经网络的每一层中的每一个节点上重复!我知道,在这样高维度的复杂度下,你的思维有点困难。不幸的是,至少目前我们只限于三维大脑。但那是另一个故事了。
非线性关系
记住,如果我们采用当前的分层神经网络,随机设置所有的权值和偏差,那么在输出节点处得到的权值函数仍然是直线的。
不管我们如何组合权重和和,我们总会得到一个线性模型……这就是目前为止数学的计算方法。
虽然建立线性关系模型可能很有趣,但这并不是非常有用。我们希望我们的神经网络能够解释复杂的非线性关系。
因此,我们将在每个节点上修改线性方程,为我们的网络增加一些非线性,我们称之为“激活函数”。
把它想象成一个“激活”我们的神经网络的函数,因为它的目的是使我们的网络从建模线性i维超平面到建模非线性i维函数。一个流行的激活函数是logistic曲线,也被称为sigmoid函数:

这个函数“压制”了我们的加权和,因此不管它们的值有多高或多低,它们最终总是在0和1之间。将我们在每个节点上的现有方程通过sigmoid函数后,我们修改后的方程为:
yₖ = σ ( vₖ )
or
yₖ = σ ( ∑ ( xᵢ × wᵢ ) + bₖ )
将此组件添加到我们的关系图中,现在我们有:

现在,我们的节点实际上已经完成了!
sigmoid函数允许我们的节点考虑多个输入之间的交互效果和非线性关系。当与网络中所有其他节点连接时,我们的神经网络获得了建模复杂非线性i维关系的能力。
一个神经网络模型之间的关系,只有三个输入可能最终会像这样:

但是,像上面显示的非线性平面这样简单的东西,可以由人类来计算。我们真的不需要一个神经网络来模拟三维空间的功能。
但是当我们开始处理越来越多的变量并进入越来越高的维度时,神经网络变得非常有用。我的意思是,我们怎么会想出一个能精确映射上千个变量的模型呢?
答案是——我们没有。这就是神经网络的作用!
让我重申:
当加权输入被加在一起并在每个节点上通过一个激活函数时,神经网络获得了建模复杂非线性i维关系的能力。
这就是为什么神经网络如此有用。
由于我们可以修改每个节点的权值和偏差,因此我们的神经网络现在在理论上应该能够学习和建模任意数量变量之间的任何关系。
直到现在我们才开始训练我们的网络!️
考虑到这一切,我们开始在每个节点上用随机的一组权重和偏差来训练我们的神经网络。
当我们向网络提供大量包含输入和正确输出的数据和训练示例时,网络尝试将输入映射到相应的输出。
输出层中最“活跃”的节点(换句话说,它返回的值比其他输出节点的加权和要高)是神经网络对给定输入集的“正确答案”的选择。
该死,这么多错误!
显然,由于我们从每个节点的随机权重和偏差开始,网络的预测从一开始就不准确。这就是我们需要训练网络的原因。
我们向网络展示我们的训练示例的正确答案,我们基本上告诉网络,看看它的预测与每次正确答案的接近程度。我们通过使用损失函数计算输出中的误差:
Error = ½ × (Actual output — Predicted Output)²
我们的目标是最小化误差以提高网络的准确性。将这个过程形象化的一个简单方法是将图形误差想象成一个向上开口的抛物线函数,其中底部的波谷代表最小的误差。
我们使用一种叫做梯度下降的方法来最小化我们的点在这个损失函数上的导数。这是一种有趣的说法,如果我们要画一条与点相切的直线,我们希望它的斜率尽可能小。
想想看,抛物线的切线斜率为0的唯一点是最底端的点,损失最小!
知道点对损失函数的导数是非常有用的因为它变得越小,误差就越小。
因此,梯度下降函数通过将神经网络的误差点向下移动到损失函数的局部最小值来帮助我们最小化损失。
在实践中,我们的损失函数不会是一个双变量抛物线,因为大多数神经网络不止有两个输入,因此也不止有两个变量。
相反,损失函数将类似于多维空间中的山和谷。因此,梯度下降函数通过最小化损失函数上的点的“梯度”或多变量导数来减少误差。
因此,与其在抛物线上降低我们的损失,不如把梯度下降的过程想象成把一个球滚下山,这个球代表了我们神经网络的误差量。
[caption id="attachment_47182" align="aligncenter" width="1200"]
 我们在这里使用线性回归模型来保持可视化的简单性。观察模型的准确性如何提高(右),因为它的点在损失函数(左)“滚下山”。[/caption]
我们在这里使用线性回归模型来保持可视化的简单性。观察模型的准确性如何提高(右),因为它的点在损失函数(左)“滚下山”。[/caption]简而言之,梯度下降法使网络能够计算出给定一组输入时,它的输出是需要更大的正值还是负值,以便在进行预测时提高网络的整体准确性。
该死的,纠正他们的错误!
一旦通过损失函数计算出误差,网络中的权值和偏差就会被修正以使误差最小化。这是通过一种叫做反向传播的方法实现的:
W(k+1) = W(k) — (Learning Rate) × (Gradient Descent Applied to Error)
其中W(k+1)表示新的权值,W(k)表示当前权值。
反向传播函数将错误从输出层向后传播到网络中的每一层。它本质上允许我们修改神经网络中节点之间的每一个权重的值,使一些节点变得比其他节点更“活跃”。
[caption id="attachment_47183" align="aligncenter" width="480"]
 可视化反向传播。图像来源于虚构到事实。[/caption]
可视化反向传播。图像来源于虚构到事实。[/caption]这些修改的目的是最小化神经网络的损失或误差。经过无数次的反复训练,损失最小化,我们的神经网络在工作中变得越来越精确,无论是识别手写数字还是推荐你下一个YouTube视频。
关键要点
- 神经网络学习输入变量和输出变量之间的关系。
- 给定足够的数据进行训练,神经网络学习从x到y的精确映射。
- 神经网络由输入层、隐藏层和输出层组成。
- 单个节点的函数可以与线性回归进行比较,其中每个节点都有一组权重和偏差。
- 神经元与线性回归模型的不同之处在于,一个节点可以接受几个加权的输入,并且一层的每个节点都向下一层的节点提供信息。这一特性使得神经网络能够模拟数十个、数百个或数千个变量之间极其复杂的关系。
- 我们使用激活函数来解释变量之间关系的非线性。
- 梯度下降用于识别和最小化神经网络中的损失,其工作原理类似于滚下丘陵和山谷的球。
- 一旦确定了损失,通过反向传播使损失最小化;输出层的错误通过微积分中的链式法则向后传播,从而调整每一层的权重和偏差。
恭喜你!
你绝对是个传奇。我没有耐心读完所有的东西(考虑到是我写的,这很有趣)。你真棒!
更重要的是,现在除了导入TensorFlow之外,您对神经网络如何工作有了更直观的理解。
我希望您学到了一些有价值的东西,我们下一篇文章再见!

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























