如何处理缺失值
2019年12月07日 由 sunlei 发表
227015
0
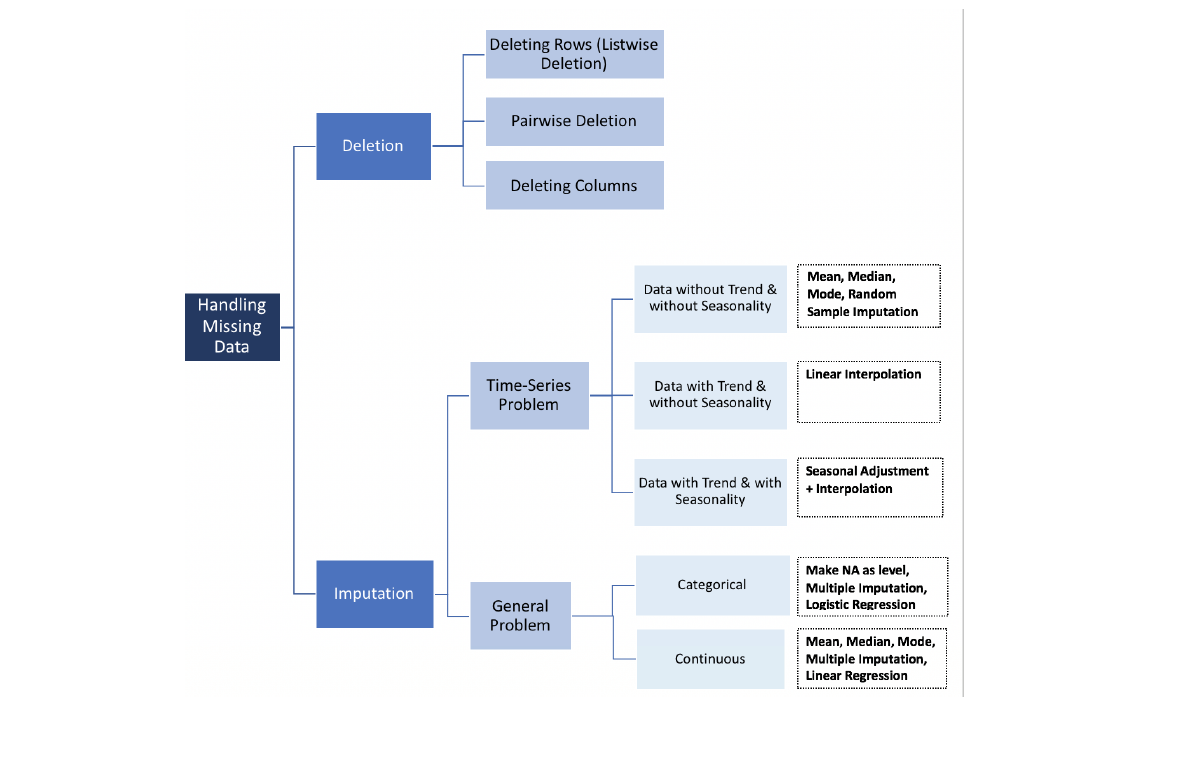
我在数据清理/探索性分析中遇到的最常见问题之一是处理缺失的值。首先,要明白没有好的方法来处理丢失的数据。根据问题的类型,我遇到过不同的数据归集解决方案-时间序列分析,ML,回归等,很难提供一个通用的解决方案。在篇文章中,我试图总结最常用的方法,并试图找到一个结构化的解决方案。
在使用数据归集方法之前,我们必须先了解数据丢失的原因。
1、随机缺失(MAR):随机缺失意味着数据点缺失的倾向与缺失的数据无关,而是与一些观察到的数据相关
2、完全随机缺失(MCAR):某个值缺失的事实与它的假设值以及其他变量的值无关
3、非随机缺失(MNAR):两个可能的原因是,缺失值取决于假设的值(例如,高薪人群通常不想在调查中透露他们的收入)或缺失值依赖于其他变量的值(例如假设女性一般不愿透露他们的年龄!此处年龄变量缺失值受性别变量影响)
在前两种情况下,根据数据的出现情况删除缺失值的数据是安全的,而在第三种情况下,删除缺失值的观察值会在模型中产生偏差。所以在移除观测结果之前,我们必须非常小心。请注意,归集并不一定会给出更好的结果。
Listwise
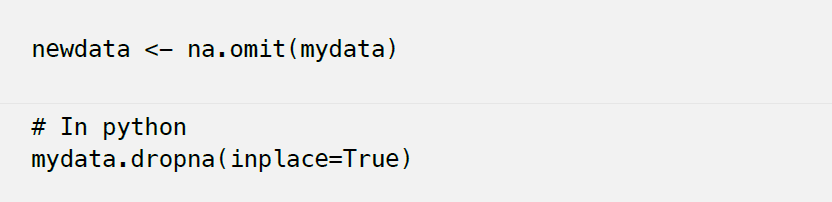
listwise deletion(complete case analysis)【列表删除(完全案例分析)】删除一个或多个缺失值的观察的所有数据。特别是如果缺少的数据仅限于少量的观察,您可以选择从分析中消除这些情况。然而,在大多数情况下,使用列表删除通常是不利的。这是因为MCAR(完全随机缺失)的假设通常很少得到支持。因此,列表删除方法产生有偏差的参数和估计。
成对
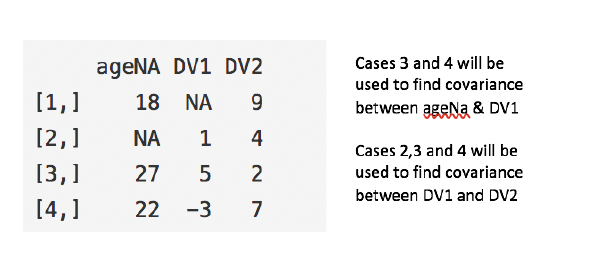
成对删除分析所有感兴趣的变量存在的情况,从而最大限度地通过分析的基础上获得的所有数据。这项技术的一个优点是它增加了你的分析能力,但它有很多缺点。它假设丢失的数据是MCAR。如果你删除成对的数据,那么你将得到不同数量的观测数据,这些数据将对模型的不同部分产生影响,这将使解释变得困难。

删除变量
在我看来,保留数据总比丢弃数据好。有时,如果数据丢失超过60%的观察结果,但只有当该变量不重要时,才可以删除变量。尽管如此,与删除变量相比,归集始终是首选。

前向观测(LOCF)和后向观测(NOCB)
这是一种分析纵向重复测量数据的常用统计方法,其中一些后续观测数据可能会丢失。纵向数据在不同的时间点跟踪相同的样本。这两种方法都会在分析中引入偏差,并且在数据有明显趋势时表现不佳
线性插值
该方法适用于具有一定趋势的时间序列,但不适用于季节数据
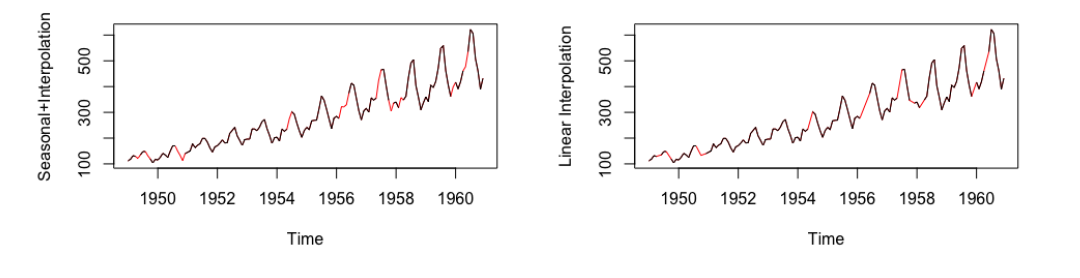
[caption id="attachment_47734" align="aligncenter" width="1041"]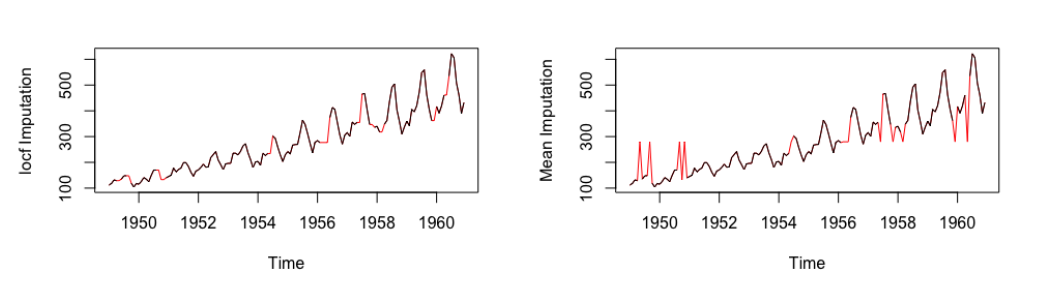 数据:Tsairgap表单库(输入),红色插值数据[/caption]
数据:Tsairgap表单库(输入),红色插值数据[/caption]

平均值、中值和模式
计算总体均值、中值或模式是一种非常基本的归集方法,它是唯一不利用时间序列特征或变量之间关系的被测函数。它很快,但有明显的缺点。一个缺点是平均估算减少了数据集中的方差。


线性回归
首先,用一个相关矩阵来识别缺少值的变量的几个预测器。在回归方程中选取最佳的预测因子作为自变量。缺少数据的变量用作因变量。使用具有预测变量完整数据的情况来生成回归方程;然后使用该方程来预测不完整情况下的缺失值。在迭代过程中,插入缺失变量的值,然后使用所有情况预测因变量。重复这些步骤,直到每个步骤的预测值之间几乎没有差别,即它们是收敛的,它“理论上”为丢失的值提供了很好的估计。然而,这种模式有几个缺点,往往大于优点。首先,因为替换的值是从其他变量中预测出来的,它们往往“非常吻合”,所以标准误差被缩小了。当回归方程中使用的变量可能不存在线性关系时,还必须假设它们之间存在线性关系。
多重替代法
1、归责: 将不完整数据集的缺失项插补M次(M=3)。请注意,估算值来自分布。模拟随机绘图不包括模型参数的不确定性。更好的方法是使用马尔可夫链蒙特卡罗((MCMC)模拟。这个步骤产生m个完整的数据集。
2、分析:分析m个完整的数据集。
3、池:将m分析结果集成到最终结果中
[caption id="attachment_47738" align="aligncenter" width="782"]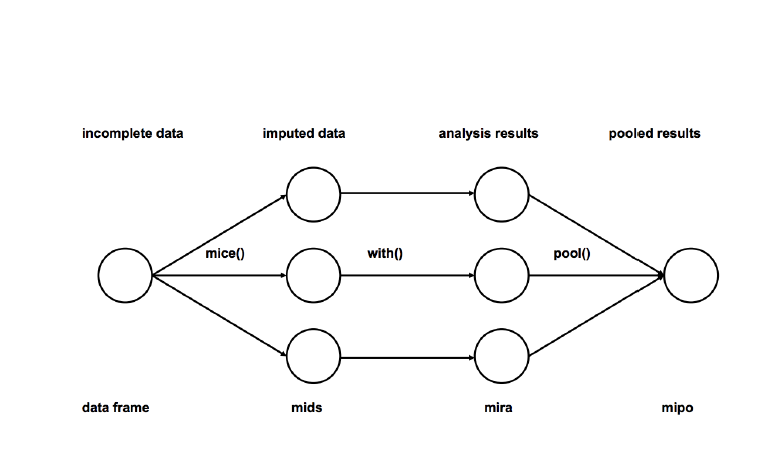 资料来源:http://www.stefvanbuuren.nl//publications/mice%20in%20R%20-%20draft.pdf[/caption]
资料来源:http://www.stefvanbuuren.nl//publications/mice%20in%20R%20-%20draft.pdf[/caption]

这是目前最受欢迎的归责方法,原因如下:
-使用方便
-无偏差(如果归责模型正确)
范畴变量的归算
1、模式归算是一种方法,但它必然会引入偏差
2、缺失的值可以单独作为一个类别处理。我们可以为缺失的值创建另一个类别,并将它们用作不同的级别。这是最简单的方法。
3、预测模型:在这里,我们创建一个预测模型来估计将替代缺失数据的值。在本例中,我们将数据集分为两组:一组没有缺失变量值(training),另一组缺失值(test)。我们可以使用逻辑回归和方差分析等方法进行预测
4、多重替代法
还有其他的机器学习技术,如XGBoost和随机森林的数据输入,但我们将讨论KNN的广泛应用。该方法根据距离测度选取k个邻域,并以其平均值作为估算值。该方法需要选择最近邻的数目和距离度量。KNN既可以预测离散属性(k个近邻中出现频率最高的值),也可以预测连续属性(k个近邻中出现频率最高的值)。
距离度量根据数据类型而变化:
KNN算法最吸引人的特性之一是它易于理解和实现。KNN的非参数特性使它在某些数据可能非常“不寻常”的情况下具有优势。
KNN算法的一个明显缺点是,在分析大型数据集时非常耗时,因为它在整个数据集中搜索类似的实例。此外,由于最近邻和最近邻之间的差异很小,在高维数据条件下,KNN的精度会严重下降。

在以上所讨论的方法中,多重归责法和KNN法被广泛使用,而多重归责法一般比较简单。
参考文献:
原文链接:https://towardsdatascience.com/how-to-handle-missing-data-8646b18db0d4
归集与删除数据
在使用数据归集方法之前,我们必须先了解数据丢失的原因。
1、随机缺失(MAR):随机缺失意味着数据点缺失的倾向与缺失的数据无关,而是与一些观察到的数据相关
2、完全随机缺失(MCAR):某个值缺失的事实与它的假设值以及其他变量的值无关
3、非随机缺失(MNAR):两个可能的原因是,缺失值取决于假设的值(例如,高薪人群通常不想在调查中透露他们的收入)或缺失值依赖于其他变量的值(例如假设女性一般不愿透露他们的年龄!此处年龄变量缺失值受性别变量影响)
在前两种情况下,根据数据的出现情况删除缺失值的数据是安全的,而在第三种情况下,删除缺失值的观察值会在模型中产生偏差。所以在移除观测结果之前,我们必须非常小心。请注意,归集并不一定会给出更好的结果。

删除
Listwise
listwise deletion(complete case analysis)【列表删除(完全案例分析)】删除一个或多个缺失值的观察的所有数据。特别是如果缺少的数据仅限于少量的观察,您可以选择从分析中消除这些情况。然而,在大多数情况下,使用列表删除通常是不利的。这是因为MCAR(完全随机缺失)的假设通常很少得到支持。因此,列表删除方法产生有偏差的参数和估计。

成对
成对删除分析所有感兴趣的变量存在的情况,从而最大限度地通过分析的基础上获得的所有数据。这项技术的一个优点是它增加了你的分析能力,但它有很多缺点。它假设丢失的数据是MCAR。如果你删除成对的数据,那么你将得到不同数量的观测数据,这些数据将对模型的不同部分产生影响,这将使解释变得困难。


删除变量
在我看来,保留数据总比丢弃数据好。有时,如果数据丢失超过60%的观察结果,但只有当该变量不重要时,才可以删除变量。尽管如此,与删除变量相比,归集始终是首选。

时间序列特定方法
前向观测(LOCF)和后向观测(NOCB)
这是一种分析纵向重复测量数据的常用统计方法,其中一些后续观测数据可能会丢失。纵向数据在不同的时间点跟踪相同的样本。这两种方法都会在分析中引入偏差,并且在数据有明显趋势时表现不佳
线性插值
该方法适用于具有一定趋势的时间序列,但不适用于季节数据

[caption id="attachment_47734" align="aligncenter" width="1041"]
 数据:Tsairgap表单库(输入),红色插值数据[/caption]
数据:Tsairgap表单库(输入),红色插值数据[/caption]
平均值、中值和模式
计算总体均值、中值或模式是一种非常基本的归集方法,它是唯一不利用时间序列特征或变量之间关系的被测函数。它很快,但有明显的缺点。一个缺点是平均估算减少了数据集中的方差。


线性回归
首先,用一个相关矩阵来识别缺少值的变量的几个预测器。在回归方程中选取最佳的预测因子作为自变量。缺少数据的变量用作因变量。使用具有预测变量完整数据的情况来生成回归方程;然后使用该方程来预测不完整情况下的缺失值。在迭代过程中,插入缺失变量的值,然后使用所有情况预测因变量。重复这些步骤,直到每个步骤的预测值之间几乎没有差别,即它们是收敛的,它“理论上”为丢失的值提供了很好的估计。然而,这种模式有几个缺点,往往大于优点。首先,因为替换的值是从其他变量中预测出来的,它们往往“非常吻合”,所以标准误差被缩小了。当回归方程中使用的变量可能不存在线性关系时,还必须假设它们之间存在线性关系。
多重替代法
1、归责: 将不完整数据集的缺失项插补M次(M=3)。请注意,估算值来自分布。模拟随机绘图不包括模型参数的不确定性。更好的方法是使用马尔可夫链蒙特卡罗((MCMC)模拟。这个步骤产生m个完整的数据集。
2、分析:分析m个完整的数据集。
3、池:将m分析结果集成到最终结果中
[caption id="attachment_47738" align="aligncenter" width="782"]
 资料来源:http://www.stefvanbuuren.nl//publications/mice%20in%20R%20-%20draft.pdf[/caption]
资料来源:http://www.stefvanbuuren.nl//publications/mice%20in%20R%20-%20draft.pdf[/caption]
这是目前最受欢迎的归责方法,原因如下:
-使用方便
-无偏差(如果归责模型正确)
范畴变量的归算
1、模式归算是一种方法,但它必然会引入偏差
2、缺失的值可以单独作为一个类别处理。我们可以为缺失的值创建另一个类别,并将它们用作不同的级别。这是最简单的方法。
3、预测模型:在这里,我们创建一个预测模型来估计将替代缺失数据的值。在本例中,我们将数据集分为两组:一组没有缺失变量值(training),另一组缺失值(test)。我们可以使用逻辑回归和方差分析等方法进行预测
4、多重替代法
KNN邻近算法
还有其他的机器学习技术,如XGBoost和随机森林的数据输入,但我们将讨论KNN的广泛应用。该方法根据距离测度选取k个邻域,并以其平均值作为估算值。该方法需要选择最近邻的数目和距离度量。KNN既可以预测离散属性(k个近邻中出现频率最高的值),也可以预测连续属性(k个近邻中出现频率最高的值)。
距离度量根据数据类型而变化:
- 连续数据:连续数据常用的距离度量有欧几里德、曼哈顿和余弦
- 分类数据:本例中一般使用汉明距离。它获取所有的分类属性,如果两个点之间的值不相同,则分别计算一个。然后,汉明距离等于值不同的属性的数量。
KNN算法最吸引人的特性之一是它易于理解和实现。KNN的非参数特性使它在某些数据可能非常“不寻常”的情况下具有优势。
KNN算法的一个明显缺点是,在分析大型数据集时非常耗时,因为它在整个数据集中搜索类似的实例。此外,由于最近邻和最近邻之间的差异很小,在高维数据条件下,KNN的精度会严重下降。

在以上所讨论的方法中,多重归责法和KNN法被广泛使用,而多重归责法一般比较简单。
参考文献:
- https://www.bu.edu/sph/les/2014/05/Marina-tech-report.pdf
- https://arxiv.org/pdf/1710.01011.pdf
- https://machinelearningmastery.com/k-nearest-neighbors-formachine-learning/
- https://kevinzakka.github.io/2016/07/13/k-nearest-neighbor/
- Time-Series Lecture at University of San Francisco by Nathaniel Stevens
原文链接:https://towardsdatascience.com/how-to-handle-missing-data-8646b18db0d4

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
股市预测初步实践与体会
热门企业
热门职位
写评论取消
回复取消






























