二、涉及到的一些数学概念

前文回顾：梯度下降背后的数学原理几何？（上）

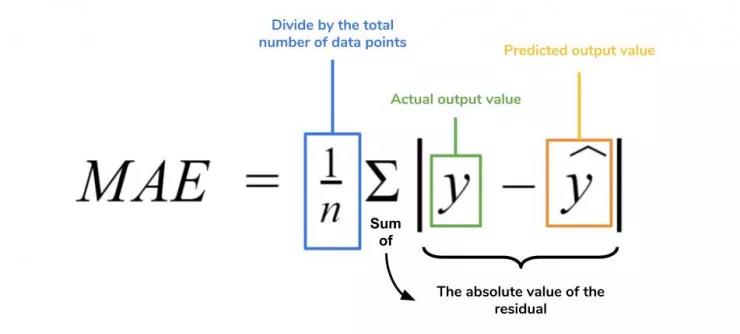
5、平均绝对误差

平均绝对误差测量的是一组预测样本中平均误差的大小，而无需评估其方向或矢量，可以通过以下公式进行建模。

6、均方误差

均方误差可找到预测值与实际值之间平均差的平方。除了最后取值为平方而不是绝对值这一点以外，均方误差与平均绝对误差 MAE 的原理基本一致。其对于部分误差值的度量标准不再是坐标系内点之间的距离，而是找到由测量点之间的距离产生的形状（通常为正方形）区域。

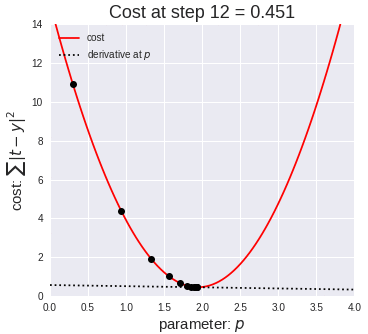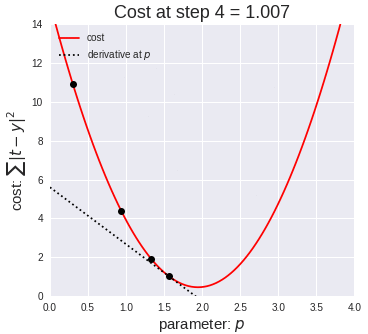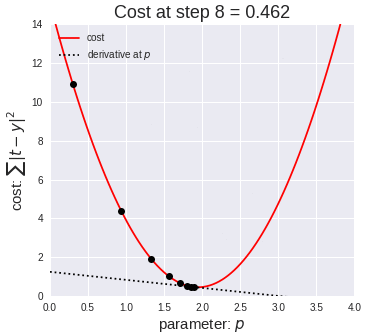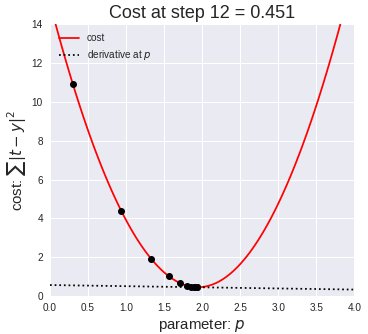
7、梯度下降（再次介绍）

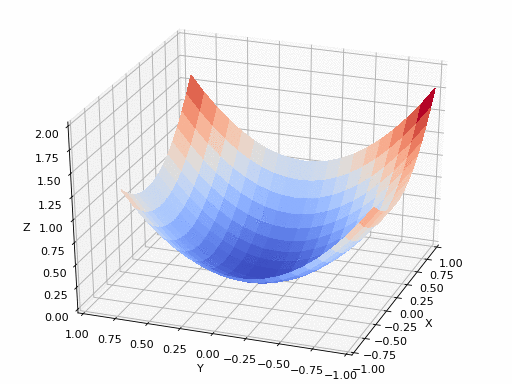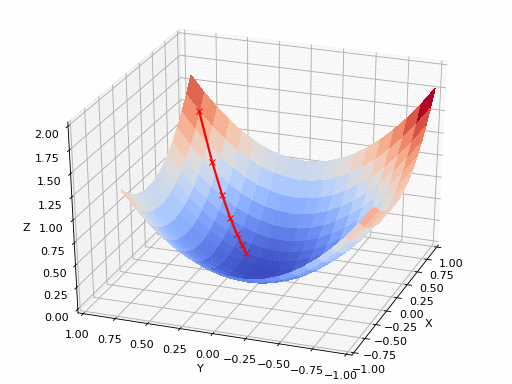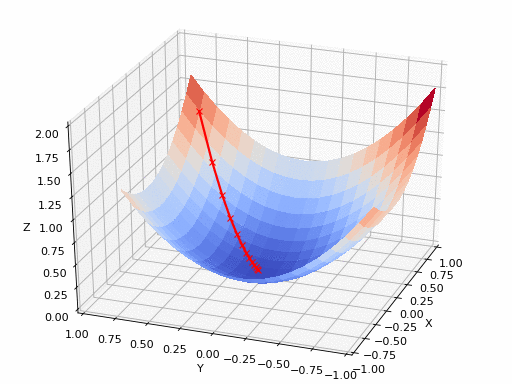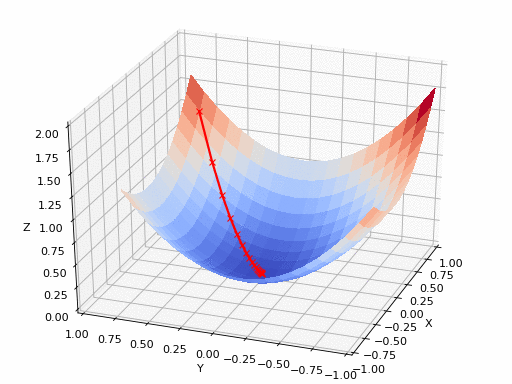
让我们看这样一个类比，以进一步了解梯度下降的直观原理！



想象一下，你站在珠穆朗玛峰峰顶上，现在要完成通往山底的任务，这听起来相当简单且直观对吧？
然而，（现在有一个你需要考虑的细节信息是——你完全是一个盲人）这里出现了一则你需要重新考虑的小信息——你是盲人。
这无疑使得任务变得更加艰巨，但目标也并非完全不可能实现。在你开始朝着更大倾斜度的方向移动前，你需要迈出一小步一小步。在你抵达山底之前，此方法需要进行无数次迭代以最终达到目的地。
这从本质上模仿了梯度下降的理念，在梯度下降中，模型通过后向传播以最终到达山的最低点。
山脉类似于在空间中绘制的数据图，行走的步长类似于学习率，感受地形陡峭程度就类似于算法计算数据集参数的梯度。
若假设正确，选择的方向会降低成本函数。山的底部代表了机器的权重的最佳值（成本函数已经被最小化）。

8、线性回归

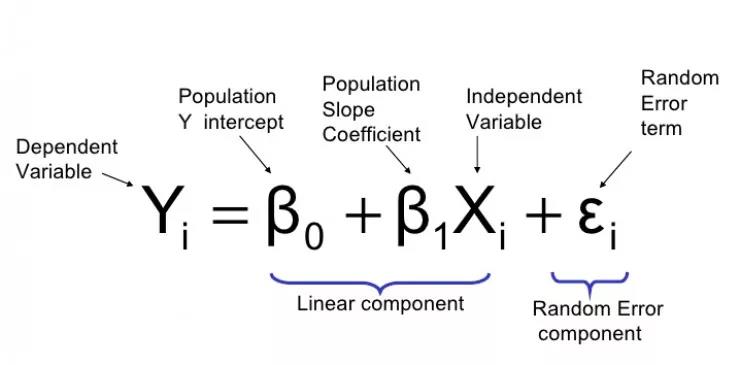
对于那些不熟悉的变量，在所有统计模型学科中常常使用回归分析来研究多变量函数之间的关系以进行预测分析。
代表期望值和实验值之间误差的线称为回归线，每个残差值都可以通过与其方差与最佳拟合线连接的垂直线段描绘出来。

下面的公式将 x 表示为输入的训练数据（参数为单变量或单输入变量），假设进行了监督学习，则 y 表示数据的标签。

让我们通过以下示例对此做进一步了解。
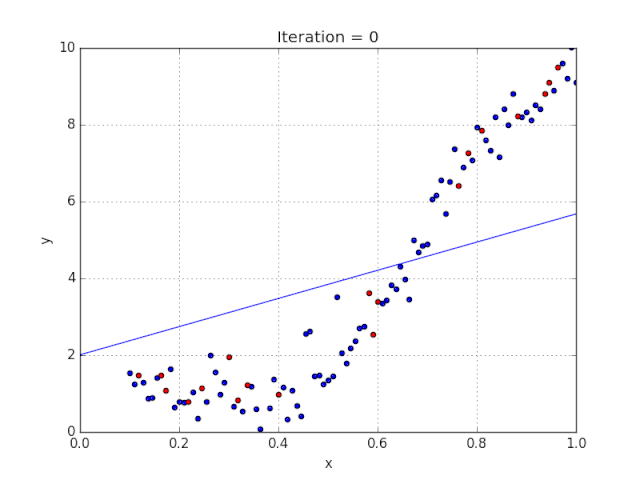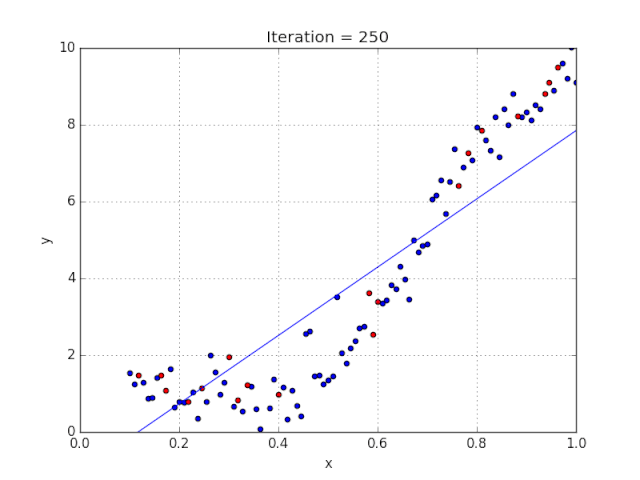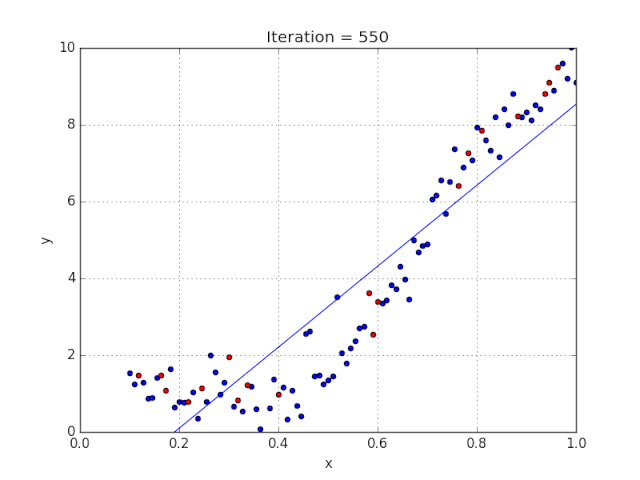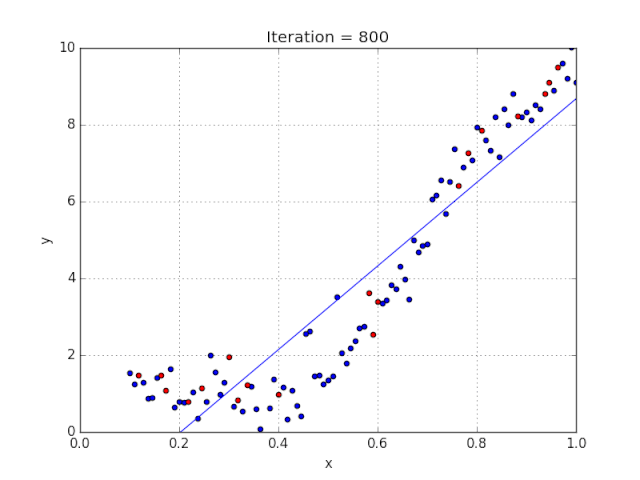
Elon 在 salesx 担任兼职市场总监，他收集了过去一年的促销工作促销活动的付款额与销售额的数据，给未来销售和促销提供一些指导性建议。
Elon认为该数据应该是线性的，所以用散点图的方式来呈现这些信息，横纵坐标分别为新客户数量和花费的成本。Elon构造了回归线，其目的是为了更好地理解和预测salesx将通过新的营销理念获得多少客户。

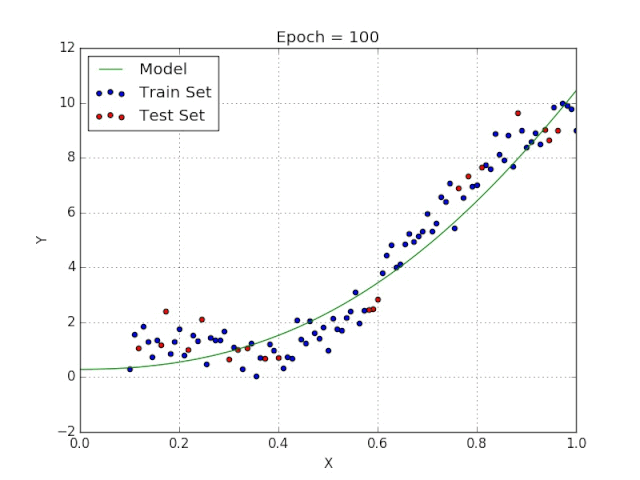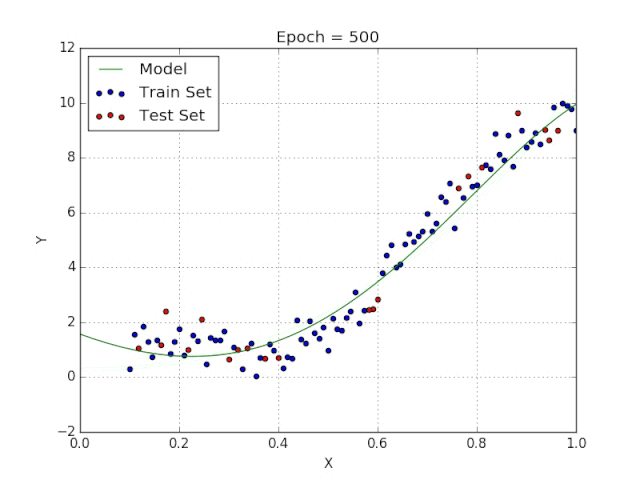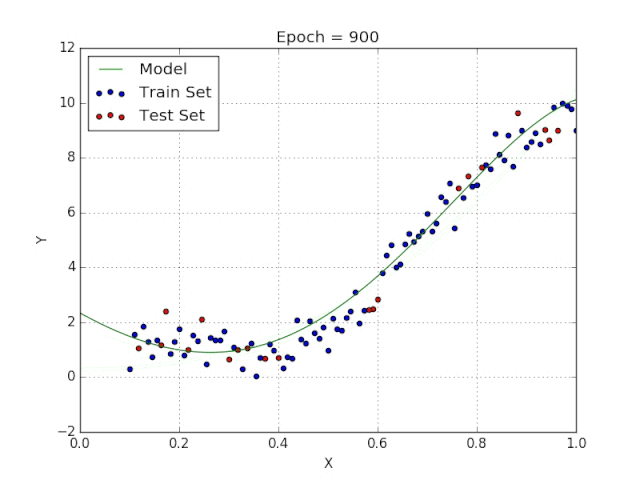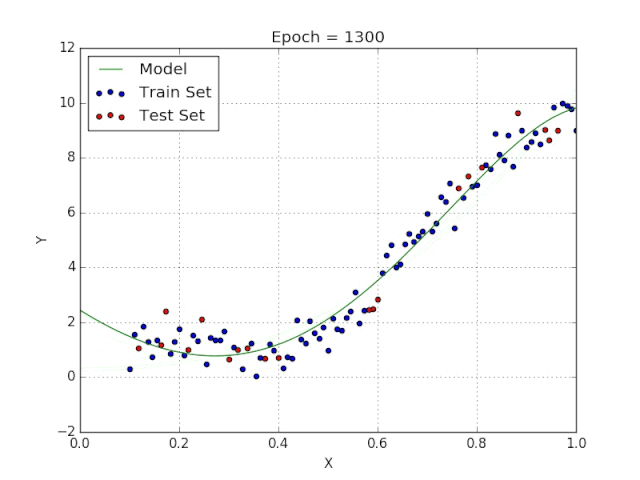
9、多项式回归

线性回归可以很好地显示数据集中两个相关变量中存在的结构和趋势。但是，考虑到线性函数的行为，而由于在非线性关系中依然可以清楚地表现出一定的相关性，它们无法将非线性的回归关系进行准确反映。
多项式回归能够对 n 次方函数之间的关系进行建模，并且可以以低于线性回归的误差函数值拟合某些数据集。
尽管多项式回归可以更好地拟合函数的曲率，并且可以最准确地表示两个变量之间的关系，但它们对异常值极为敏感，那些异常值很容易造成数据偏离。





原文链接：https://medium.com/datadriveninvestor/the-math-and-intuition-behind-gradient-descent-13c45f367a11