如何利用图卷积网络对图进行深度学习(下)
2020年01月27日 由 sunlei 发表
704357
0
前文回顾:如何利用图卷积网络对图进行深度学习(上)
我们现在结合了自循环和规范化技巧。此外,我们将重新引入我们先前丢弃的权重和激活函数,以简化讨论。
首先要做的是计算权重。注意,这里D_hat是A_hat = A + I的次数矩阵,即,具有强制自循环的A的度矩阵。
如果我们想降低输出特征表示的维数,我们可以减小权重矩阵W的大小:
我们选择保留特征表示的维数,并应用ReLU激活函数。
瞧!一个完整的隐含层与邻接矩阵,输入特征,权值和激活功能!
现在,最后,我们可以将图卷积网络应用于实图。我将向您展示如何生成我们在文章早期看到的功能表示。
Zachary空手道俱乐部
Zachary空手道俱乐部是一个常用的社交网络,其中的节点代表空手道俱乐部的成员,并边缘他们的相互关系。在空手道俱乐部学习时,管理者和教练发生了冲突,导致俱乐部一分为二。下图显示了网络的图形表示,节点根据俱乐部的哪个部分进行标记。管理员和讲师分别标有“A”和“I”。
[caption id="attachment_49996" align="aligncenter" width="1200"] Zachary空手道俱乐部[/caption]
Zachary空手道俱乐部[/caption]
现在让我们建立图卷积网络。我们实际上不会训练网络,只是随机初始化它,以生成我们在本文开头看到的特性表示。我们将使用networkx,它有一个容易获得的俱乐部的图形表示,并计算A_hat和D_hat矩阵。
接下来,我们将随机初始化权值。
堆叠GCN层。这里我们只使用身份矩阵作为特征表示,即每个节点被表示为一个热编码的分类变量。
我们提取特征表示。
瞧!将Zachary空手道俱乐部的社区很好地分隔开的特征表示。我们还没开始训练呢!
[caption id="attachment_49997" align="aligncenter" width="1200"]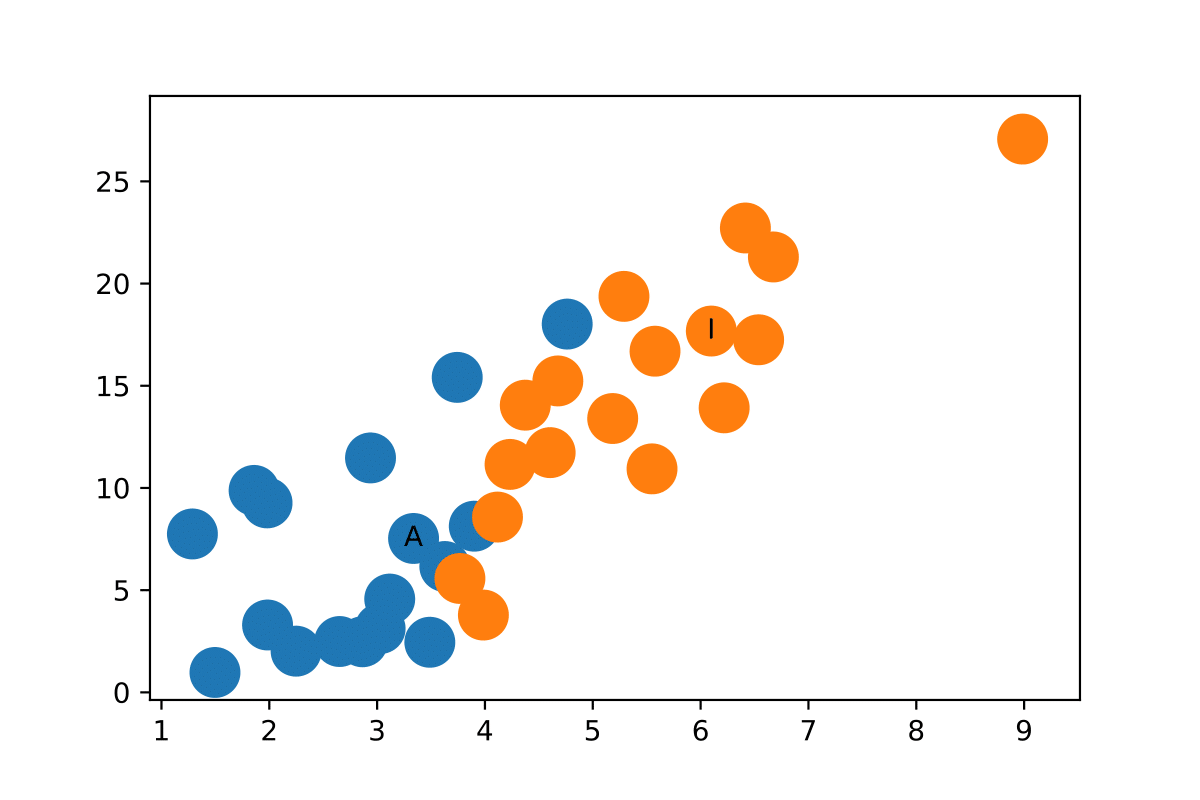 Zachary空手道俱乐部节点的特征表示[/caption]
Zachary空手道俱乐部节点的特征表示[/caption]
我应该注意的是,对于这个例子,随机初始化的权重很可能在X或Y轴上给出0个值作为Relu函数的结果,因此需要几个随机初始化来产生上面的图。
在这篇文章中,我对图卷积网络做了一个高级的介绍,并说明了GCN中每一层节点的特征表示是如何基于其邻域的集合的。我们看到了如何使用numpy来构建这些网络,以及它们是多么强大:即使是随机初始化的GCNs也可以在Zachary的空手道俱乐部中社区分离。
参考文献
[1] Thomas Kipf关于图形卷积网络的博客文章。
[2] 论文Thomas-Kipf和Max-Welling将图卷积网络称为半监督分类。
原文链接:https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780
把所有的东西放在一起
我们现在结合了自循环和规范化技巧。此外,我们将重新引入我们先前丢弃的权重和激活函数,以简化讨论。
把权重加回来
首先要做的是计算权重。注意,这里D_hat是A_hat = A + I的次数矩阵,即,具有强制自循环的A的度矩阵。
In [45]: W = np.matrix([
[1, -1],
[-1, 1]
])
D_hat**-1 * A_hat * X * W
Out[45]: matrix([
[ 1., -1.],
[ 4., -4.],
[ 2., -2.],
[ 5., -5.]
])
如果我们想降低输出特征表示的维数,我们可以减小权重矩阵W的大小:
In [46]: W = np.matrix([
[1],
[-1]
])
D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
[4.],
[2.],
[5.]]
)
添加激活函数
我们选择保留特征表示的维数,并应用ReLU激活函数。
In [51]: W = np.matrix([
[1, -1],
[-1, 1]
])
relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]])
瞧!一个完整的隐含层与邻接矩阵,输入特征,权值和激活功能!
回到现实
现在,最后,我们可以将图卷积网络应用于实图。我将向您展示如何生成我们在文章早期看到的功能表示。
Zachary空手道俱乐部
Zachary空手道俱乐部是一个常用的社交网络,其中的节点代表空手道俱乐部的成员,并边缘他们的相互关系。在空手道俱乐部学习时,管理者和教练发生了冲突,导致俱乐部一分为二。下图显示了网络的图形表示,节点根据俱乐部的哪个部分进行标记。管理员和讲师分别标有“A”和“I”。
[caption id="attachment_49996" align="aligncenter" width="1200"]
 Zachary空手道俱乐部[/caption]
Zachary空手道俱乐部[/caption]建立GCN
现在让我们建立图卷积网络。我们实际上不会训练网络,只是随机初始化它,以生成我们在本文开头看到的特性表示。我们将使用networkx,它有一个容易获得的俱乐部的图形表示,并计算A_hat和D_hat矩阵。
from networkx import karate_club_graph, to_numpy_matrix
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))
接下来,我们将随机初始化权值。
W_1 = np.random.normal(
loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
loc=0, size=(W_1.shape[1], 2))
堆叠GCN层。这里我们只使用身份矩阵作为特征表示,即每个节点被表示为一个热编码的分类变量。
def gcn_layer(A_hat, D_hat, X, W):
return relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2
我们提取特征表示。
feature_representations = {
node: np.array(output)[node]
for node in zkc.nodes()}瞧!将Zachary空手道俱乐部的社区很好地分隔开的特征表示。我们还没开始训练呢!
[caption id="attachment_49997" align="aligncenter" width="1200"]
 Zachary空手道俱乐部节点的特征表示[/caption]
Zachary空手道俱乐部节点的特征表示[/caption]我应该注意的是,对于这个例子,随机初始化的权重很可能在X或Y轴上给出0个值作为Relu函数的结果,因此需要几个随机初始化来产生上面的图。
结论
在这篇文章中,我对图卷积网络做了一个高级的介绍,并说明了GCN中每一层节点的特征表示是如何基于其邻域的集合的。我们看到了如何使用numpy来构建这些网络,以及它们是多么强大:即使是随机初始化的GCNs也可以在Zachary的空手道俱乐部中社区分离。
参考文献
[1] Thomas Kipf关于图形卷积网络的博客文章。
[2] 论文Thomas-Kipf和Max-Welling将图卷积网络称为半监督分类。
原文链接:https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
迎接数据加密的新变化
热门企业
热门职位
写评论取消
回复取消






























