介绍

加深对深度学习模型和损失函数背后的数学理解的最佳方法，也是提高PyTorch技能的好方法之一，就是习惯自己实现深度学习论文。

书籍和博客文章可以帮助你开始编码并学习机器学习/深度学习的基础知识。然而，在学习了其中几本书并熟练掌握领域中的常规任务后，你很快就会意识到在学习旅程中你是孤军奋战的，而且你会发现大多数在线资源都很无聊且过于浅显。然而，如果你能够随着新的深度学习论文的发布而学习并理解其中所需的数学部分，并且你是一个能够将它们实现为高效代码的有能力的编码者，那么你将能够不断跟上该领域的最新动态并学习新的思想。

对比损失实现

我将使用一个例子来介绍我的例程和我在深度学习论文中实现数学的步骤：SimCLR论文中的对比损失。

这是损失的数学公式：



仅仅是这个公式的外观就可能让人望而生畏！你可能会认为在GitHub上一定有很多现成的PyTorch实现，是的，网上有几十种实现方法。然而，我认为这是练习这项技能的一个很好的例子，可以作为一个很好的起点。

用代码实现数学的步骤

我将论文中的数学实现为高效的PyTorch代码的例程如下：

1. 理解数学，用简单的术语解释

2. 使用简单的Python“for”循环实现初始版本，目前没有花哨的矩阵乘法

3. 将你的代码转换为高效的矩阵友好型PyTorch代码

好的，让我们直接进入第一步。

第一步：理解数学并用简单的术语解释它

我假设你们有基本的线性代数知识并且熟悉数学符号。

在上面的段落中，公式增加了更多的上下文，在SimCLR学习策略中，你从N个图像开始，并将每个图像转换2次，以获得这些图像的增强视图(现在是2*N个图像)。然后，你将这2 * N张图像通过一个模型来得到每一张图像的嵌入向量。现在，你想要使同一图像的两个增广视图(一个正对)的嵌入向量在嵌入空间中更接近(并对所有其他正对做同样的事情)。测量两个向量相似度的一种方法是使用余弦相似度，其定义为sim(u, v)。

简单来说，公式所描述的是，对于我们批处理中的每个项目，即图像的一个增强视图的嵌入，(记住：批处理包含不同图像的增强视图的所有嵌入→如果开始w/ N图像，批处理的大小为2*N)，我们首先找到该图像的另一个增强视图的嵌入，使其成为正对。然后，我们计算这两个嵌入的余弦相似度并对其求幂(公式的分子)。然后，我们开始计算第一个嵌入向量构建的所有其他对的余弦相似度的指数(除了与自身的对，这是1[k!=i]在公式中表示)，我们把它们加起来形成分母。我们现在可以把分子除以分母然后取自然对数，然后把符号翻转过来！现在，我们损失了批次中的第一个项目。我们只需要对批处理中的所有其他项重复相同的过程，然后取平均值，以便能够调用PyTorch的.backward()方法来计算梯度。

步骤2：使用简单的Python代码和“for”循环来实现它

import torch

import torch.nn.functional as F



# contains A1 and B1 embeddings

aug_views_1 = torch.tensor([[0.5, 0.1, -0.9],

                           [-0.1, 0.2, -0.5]])



# contains A2 and B2 embeddings

aug_views_2 = torch.tensor([[0.2, 0.15, -0.8],

                           [-0.5, 0.3, -0.01]])



projections = torch.cat([aug_views_1, aug_views_2], dim=0)

projections = F.normalize(projections, dim=-1)



# this keeps the relation of the augmented views using

# indexes in the concatenated projection tensor.

pos_pairs = {0: 2, 1: 3, 2: 0, 3: 1} # means: vector in index 0 and index 2 are a positive pair, and so on.

temperature = 0.05



losses = []

for i, vector in enumerate(projections):

    denom = []

    pos_pair_vector = projections[pos_pairs[i]]

    sim = vector @ pos_pair_vector.T / temperature

    non_i_idxs = [k for k in range(len(projections)) if k != i]



    for k in non_i_idxs:

        denom_sim = vector @ projections[k].T / temperature

        denom.append(denom_sim)



loss = -torch.log(sim.exp() / torch.tensor(denom).exp().sum())

losses.append(loss)



print(torch.tensor(losses).mean())

让我们看一下代码。假设我们有两个图像：A和B。变量aug_views_1保存这两个图像(A1和B1)的一个增强视图的嵌入(每个大小为3)，与aug_views_2 (A2和B2)相同；因此，两个矩阵的第一项都与图像A相关，两个矩阵的第二项都与图像B相关。我们将两个矩阵连接到投影矩阵中(其中有4个向量：A1, B1, A2, B2)。

为了保持投影矩阵中向量的关系，我们定义了pos_pairs字典来存储连接矩阵中相关的两项元素。

正如你在接下来的代码中看到的，我在for循环中遍历投影矩阵中的项，我用字典找到它的相关向量，然后我计算余弦相似度。你可能想知道为什么不除以向量的大小，正如余弦相似度公式所建议的那样。关键是在开始循环之前，使用F.normalize 函数，我将投影矩阵中的所有向量标准化使其大小为1。所以不需要除以计算余弦相似度的直线的长度。

在构建我们的分子之后，我将找到批处理中向量的所有其他索引(除了相同的索引i)，以计算构成分母的余弦相似度。最后，我通过分子除以分母，应用log函数，翻转符号来计算损失。确保使用代码来理解每行中发生的事情。

步骤3：将其转换为高效的矩阵友好型PyTorch代码

以前的python实现的问题是，它太慢了，无法在我们的训练管道中使用；我们需要摆脱缓慢的“for”循环，并将其转换为矩阵乘法和数组操作，以利用并行化能力。

import torch

import torch.nn.functional as F



batch_1 = torch.tensor([[0.5, 0.1, -0.9],

                       [-0.1, 0.2, -0.5]])



# giving arbitrary class indexes to the A1 and B1 images

labels_1 = torch.tensor([0, 1])



batch_2 = torch.tensor([[0.2, 0.15, -0.8],

                       [-0.5, 0.3, -0.01]])



# giving the same arbitrary class indexes to the A2 and B2 images

labels_2 = torch.tensor([0, 1])

temperature = 0.05



projections = torch.cat([batch_1, batch_2], dim=0)

labels = torch.cat([labels_1, labels_2], dim=0)



projections = F.normalize(projections, dim=-1)



sim_matrix = projections @ projections.T / temperature

sim_matrix = torch.exp(sim_matrix)



# creating a mask for the positive pairs in our similarity matrix

mask = torch.eq(labels.unsqueeze(1), labels.unsqueeze(0))

mask = mask.float() - torch.eye(labels.shape[0])



numerator = (sim_matrix * mask).sum(dim=-1)

denominator = sim_matrix.sum(dim=-1) - sim_matrix.diag()

loss = -torch.log(numerator / denominator)



print(loss.mean())

让我们看看这段代码片段中发生了什么。这一次，我引入了labels_1和labels_2张量来编码这些图像所属的任意类，因为我们需要一种方法来编码A1, A2和B1, B2图像之间的关系。无论你选择标签0和1还是选择标签5和8，都没有关系。

在连接嵌入和标签之后，我们首先创建一个包含所有可能对的余弦相似度的sim_matrix。



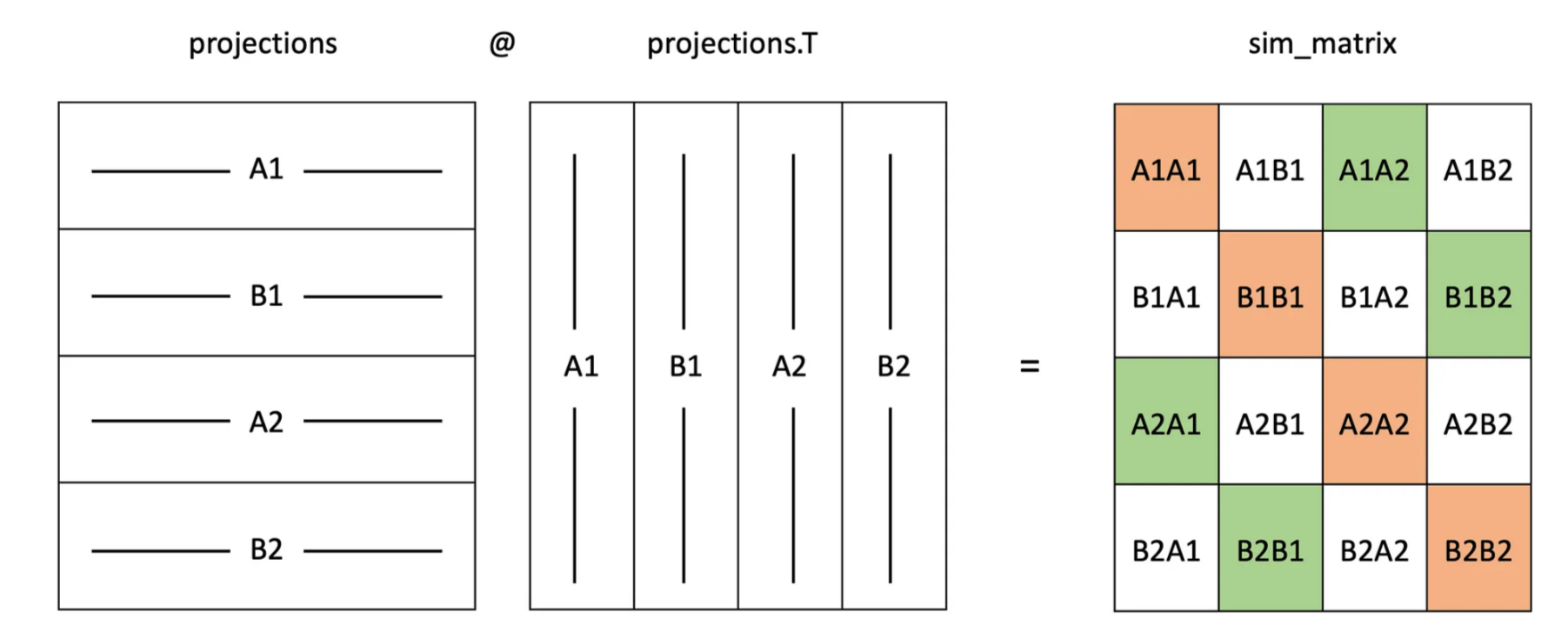
上面的可视化是你所需要的，来理解代码是如何工作的，以及为什么我们在那里做这些步骤。考虑sim_matrix的第一行，我们可以计算批次中第一项(A1)的损失如下：我们需要将A1A2(取幂)除以A1B1、A1A2、A1B2(每个先取幂)的和，并将结果保存在存储所有损失的张量的第一项中。因此，我们需要首先制作一个蒙版来找到上面可视化中的绿色单元格。定义变量mask的两行代码就是这样做的。分子是通过将我们的sim_matrix乘以我们刚刚创建的掩码来计算的，然后将每行的项相加(掩码后，每行中只有一个非零项；即绿色单元格)。为了计算分母，我们需要对每一行求和，忽略对角线上的橙色单元格。为此，我们将使用PyTorch张量的.diag()方法。其余的不言自明!

使用人工智能助手(ChatGPT, Copilot等)来执行公式

我们有很好的工具来帮助我们理解和实现深度学习论文中的数学。例如，你可以要求ChatGPT(或其他类似的工具)在PyTorch中实现代码，然后给出论文中的公式。根据我的经验，如果你能够以某种方式实现python -for-loop的实现步骤，那么ChatGPT可能是最有帮助的，并且可以在较少的跟踪和错误中提供最佳的最终答案。将这个简单的实现交给ChatGPT，并要求它将其转换为仅使用矩阵乘法和张量操作的高效PyTorch代码；你会对答案感到惊讶的。

 

来源：https://medium.com/towards-data-science/implementing-math-in-deep-learning-papers-into-efficient-pytorch-code-simclr-contrastive-loss-be94e1f63473