介绍

在本文中，我们将学习如何使用简单而现代的C++来编码的深度学习算法，如卷积、反向传播、激活函数、优化器、深度神经网络等。

卷积

卷积是信号处理领域的老朋友。最初，它的定义如下:



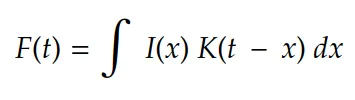
在机器学习术语中：

1. I(…)通常被称为输入

2. K(…)为核

3. F(…)作为I(x)给定K的特征映射。

考虑多维离散域，我们可以将积分转化为如下的求和：



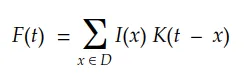
最后，对于二维数字图像，我们可以将其改写为：



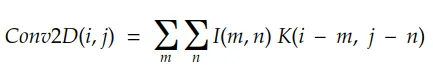
下面的例子是理解卷积的一个更简单的方法：



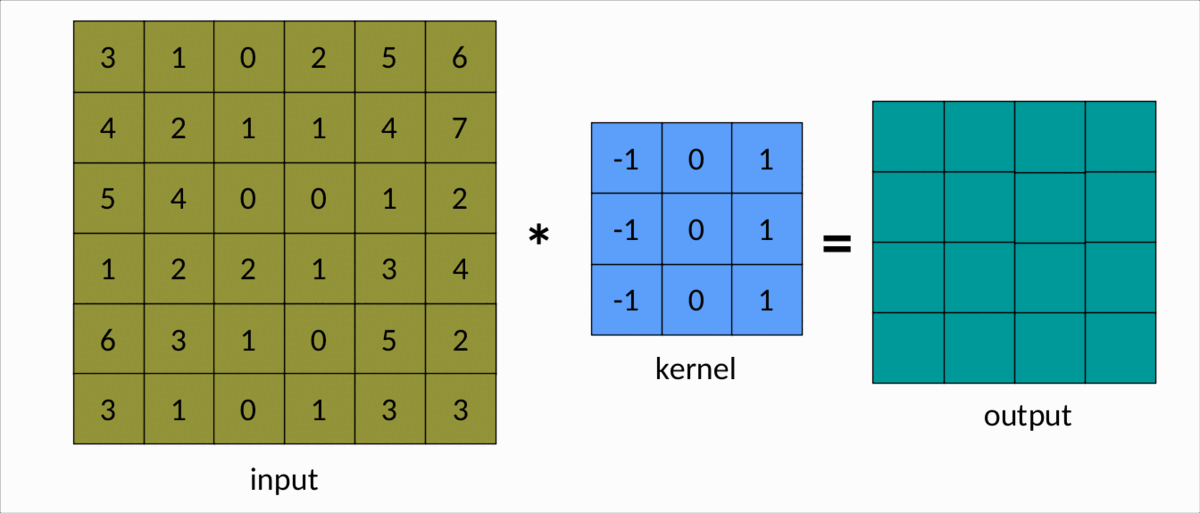
我们可以很容易地看到，卷积核在输入矩阵上滑动，生成另一个矩阵作为输出。这是卷积的简单情况，称为有效卷积。在这种情况下，输出矩阵的维度Output由以下公式决定：

dim(Output) = (m-k+1, n-k+1)

解析：

1. m和n分别是输入矩阵的行数和列数

2. k是平方核的大小。

使用循环编码2D卷积

实现卷积最直观的方法是使用循环：

auto Convolution2D = [](const Matrix &input, const Matrix &kernel)

{

    const int kernel_rows = kernel.rows();

    const int kernel_cols = kernel.cols();

    const int rows = (input.rows() - kernel_rows) + 1;

    const int cols = (input.cols() - kernel_cols) + 1;



    Matrix result = Matrix::Zero(rows, cols);



    for (int i = 0; i < rows; ++i) 

    {

        for (int j = 0; j < cols; ++j) 

        {

             double sum = input.block(i, j, kernel_rows, kernel_cols).cwiseProduct(kernel).sum();

             result(i, j) = sum;

        }

    }



    return result;

};

我们在列和行上滑动内核，对每一步应用内积。现在，我们可以这样简单地使用它：

#include 

#include 



using Matrix = Eigen::MatrixXd;



auto Convolution2D = ...;



int main(int, char **) 

{

    Matrix kernel(3, 3);

    kernel << 

       -1, 0, 1,

       -1, 0, 1,

       -1, 0, 1;



    std::cout << "Kernel:\n" << kernel << "\n\n";



    Matrix input(6, 6);

    input << 3, 1, 0, 2, 5, 6,

        4, 2, 1, 1, 4, 7,

        5, 4, 0, 0, 1, 2,

        1, 2, 2, 1, 3, 4,

        6, 3, 1, 0, 5, 2,

        3, 1, 0, 1, 3, 3;



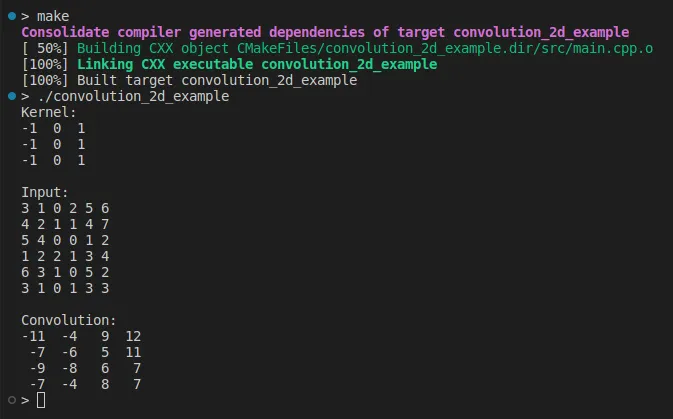
    std::cout << "Input:\n" << input << "\n\n";



    auto output = Convolution2D(input, kernel);

    std::cout << "Convolution:\n" << output << "\n";



    return 0;

}

 

填充

在上面的例子中，我们注意到输出矩阵总是小于输入矩阵。有时，这种减少是好的，有时是坏的。我们可以通过在输入矩阵周围添加填充来避免这种减少:



卷积中padding的结果如下所示：



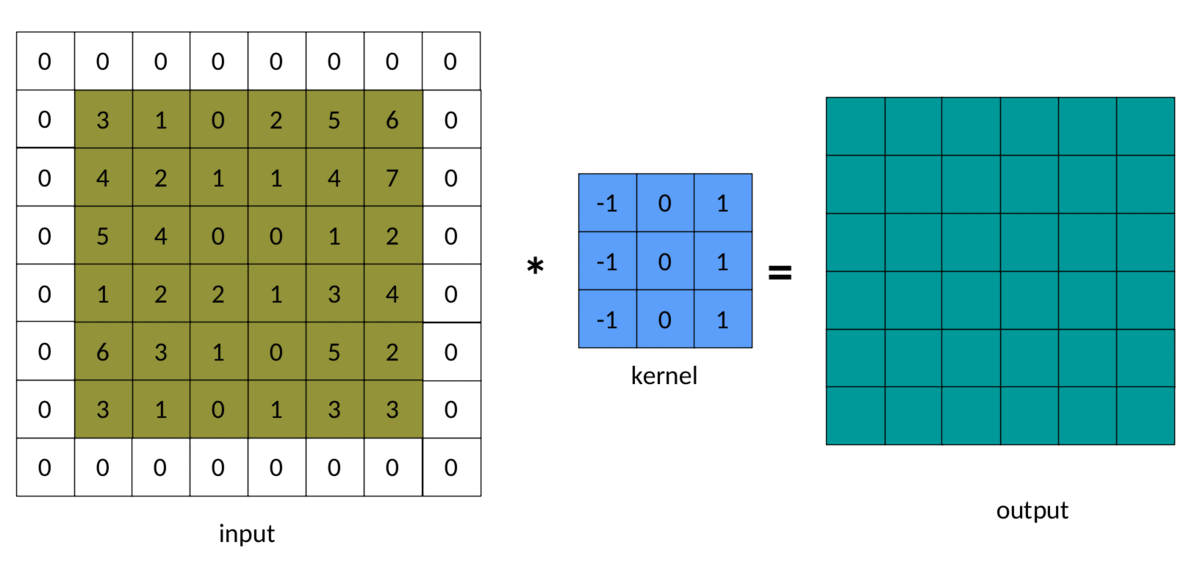
实现填充卷积的一种简单方法如下：

auto Convolution2D = [](const Matrix &input, const Matrix &kernel, int padding)

{

     int kernel_rows = kernel.rows();

     int kernel_cols = kernel.cols();

     int rows = input.rows() - kernel_rows + 2*padding + 1;

     int cols = input.cols() - kernel_cols + 2*padding + 1;



     Matrix padded = Matrix::Zero(input.rows() + 2*padding, input.cols() + 2*padding);

     padded.block(padding, padding, input.rows(), input.cols()) = input;



     Matrix result = Matrix::Zero(rows, cols);



     for(int i = 0; i < rows; ++i) 

     {

         for(int j = 0; j < cols; ++j) 

         {

             double sum = padded.block(i, j, kernel_rows, kernel_cols).cwiseProduct(kernel).sum();

             result(i, j) = sum;

         }

     }



     return result;

};

这段代码很简单，但内存使用成本高。注意，我们正在对输入矩阵进行完整的复制，以创建一个填充版本：

Matrix padded = Matrix::Zero(input.rows() + 2*padding, input.cols() + 2*padding);

padded.block(padding, padding, input.rows(), input.cols()) = input;

更好的解决方案是使用指针来控制切片和内核边界：

auto Convolution2D_v2 = [](const Matrix &input, const Matrix &kernel, int padding)

{

     const int input_rows = input.rows();

     const int input_cols = input.cols();

     const int kernel_rows = kernel.rows();

     const int kernel_cols = kernel.cols();



     if (input_rows < kernel_rows) throw std::invalid_argument("The input has less rows than the kernel");

     if (input_cols < kernel_cols) throw std::invalid_argument("The input has less columns than the kernel");

 

     const int rows = input_rows - kernel_rows + 2*padding + 1;

     const int cols = input_cols - kernel_cols + 2*padding + 1;



     Matrix result = Matrix::Zero(rows, cols);



     auto fit_dims = [&padding](int pos, int k, int length) 

     {

          int input = pos - padding;

          int kernel = 0;

          int size = k;

          if (input < 0) 

          {

              kernel = -input;

              size += input;

              input = 0;

          }

          if (input + size > length) 

          {

              size = length - input;

          }

          return std::make_tuple(input, kernel, size);

     };



     for(int i = 0; i < rows; ++i) 

     {

          const auto [input_i, kernel_i, size_i] = fit_dims(i, kernel_rows, input_rows);

          for(int j = 0; size_i > 0 && j < cols; ++j) 

          {

               const auto [input_j, kernel_j, size_j] = fit_dims(j, kernel_cols, input_cols);

               if (size_j > 0) 

               {

                    auto input_tile = input.block(input_i, input_j, size_i, size_j);

                    auto input_kernel = kernel.block(kernel_i, kernel_j, size_i, size_j);

                    result(i, j) = input_tile.cwiseProduct(input_kernel).sum();

               }

          }

     }

     return result;

};

这段新代码要好得多，因为这里我们没有分配临时内存来保存填充的输入。然而，它仍然可以改进。调用input.block(…)和kernel.block(…)也会消耗内存。

一个解决方案是使用CwiseNullaryOp block(…)替换它们。

我们可以这样运行填充卷积：

#include 



#include 

using Matrix = Eigen::MatrixXd;

auto Convolution2D = ...; // or Convolution2D_v2



int main(int, char **) 

{

    Matrix kernel(3, 3);

    kernel << 

        -1, 0, 1,

        -1, 0, 1,

        -1, 0, 1;

    std::cout << "Kernel:\n" << kernel << "\n\n";



    Matrix input(6, 6);

    input << 

        3, 1, 0, 2, 5, 6,

        4, 2, 1, 1, 4, 7,

        5, 4, 0, 0, 1, 2,

        1, 2, 2, 1, 3, 4,

        6, 3, 1, 0, 5, 2,

        3, 1, 0, 1, 3, 3;

    std::cout << "Input:\n" << input << "\n\n";



    const int padding = 1;

    auto output = Convolution2D(input, kernel, padding);

    std::cout << "Convolution:\n" << output << "\n";



    return 0;

}

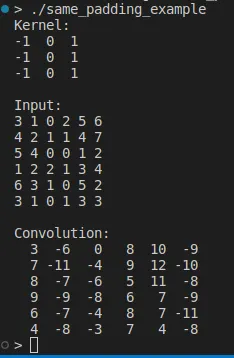
注意，现在输入和输出矩阵具有相同的维数。因此，它被称为same填充。默认填充模式，即不填充，通常称为有效填充。我们的代码允许相同的，有效的或任何非负填充。

内核

在深度学习模型中，核通常是奇数平方矩阵，如3x3、5x5、11x11等。有些核函数非常有名，比如Sobel的滤波器:



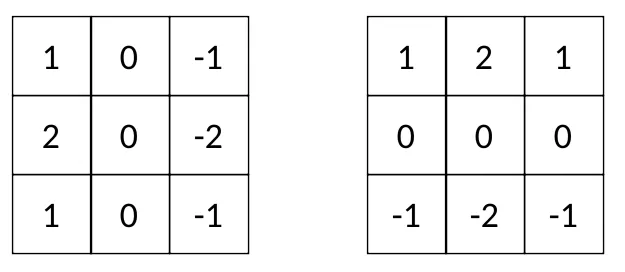
更容易看到每个 Sobel 过滤器对图像的影响：



Gy表示水平边缘，Gx表示垂直边缘。因此， Sobel 核Gx和Gy通常被称为“边缘检测器”。

边缘是图像的基本特征，如纹理、亮度、颜色等。现代计算机视觉的关键是使用算法直接从数据中自动找到Sobel滤波器等核。或者，使用更好的术语，通过迭代训练过程拟合核。

结论

在本文中，我们编写了一个2D卷积，并使用Sobel滤波器作为将这个卷积应用于图像的示例。卷积在深度学习中起着核心作用。它们被广泛应用于当今每个实际机器学习模型中。

参考资料

1. 《深度学习卷积算法指南》

2. 《深度学习书籍》，Goodfellow

3. 《神经网络和深度学习：教科书》，Aggarwal

4. 《计算机视觉：算法与应用》，Szeliski

5. 《信号与系统》，Roberts

 

来源：https://medium.com/towards-artificial-intelligence/deep-learning-from-scratch-in-modern-c-convolutions-5c55598473e9