机器学习中的梯度下降的简单指南
2023年08月01日 由 Susan 发表
199547
0
这篇文章是“解密人工智能”系列文章的一部分,旨在澄清围绕人工智能的术语。
深度学习模型以各种形式存在,每种形式都针对特定任务进行了定制。从密集层到卷积神经网络(CNN),循环神经网络(RNN),以及更近期的transformer,深度学习的领域是多样且引人入胜的。然而,在这种多样性背后存在着一条将这些模型联系在一起的共同线索-梯度下降的原则,即训练机器学习模型的技术。
深度学习的数学基础常常令人望而却步。Ronald T. Kneusel的《深度学习数学》,深入探讨了深度学习的数学复杂性,并通过示例、Python代码和图示来使其易于理解。
在本文中,我们将试图揭秘梯度下降,而不深入探讨数学细节。本文汲取了《深度学习数学》第11章的灵感,该章全面解释了梯度下降。对于更深入的理解,强烈推荐阅读整本书。它是对深度学习数学感兴趣的任何人的宝贵资源。
梯度下降背后的一般思想是通过迭代调整机器学习模型的参数,以最小化其错误。错误通过损失函数计算,损失函数计算模型预测值与实际值之间的差异,也被称为基准真值。换句话说,梯度下降的目标是找到损失函数的最小值。
梯度下降的基本思想是通过迭代地调整机器学习模型的参数,以最小化其错误。错误是通过损失函数计算得出的,它计算模型预测值与实际值(也称为基准真值)之间的差异。换句话说,梯度下降的目标是找到损失函数的最小值。
为了理解梯度下降的工作原理,想象一下你正盲目地尝试找到山谷中的最低点。你可以感受到脚下的坡度,并决定往哪个方向前进。你迈出一步,再次感受坡度,并调整你的方向。
这实质上就是梯度下降的工作方式。它从一个预测开始,计算错误,并根据损失函数的斜率调整模型的参数。通过重复这个过程,模型学习逼近基础数据的分布。
梯度下降中的“梯度”是指损失函数相对于模型参数的斜率。由于我们想要最小化误差,所以我们沿着斜率的相反方向前进,因此称之为“下降”。
为了理解梯度下降的工作原理,让我们考虑一个简单的一维问题。假设我们有一个具有单个参数x的机器学习模型。我们的目标是找到最小化损失函数的x的值,损失函数计算模型的预测值与实际值之间的误差。
假设数据的基础函数是f(x) = 6x^2 – 12x + 3。理论上,我们可以通过将一阶导数设置为零并解出x来找到函数的最小值。然而,在现实世界的应用中,问题往往非常复杂,我们事先不知道函数的形式,无法通过解析的方法来求解。这就是梯度下降发挥作用的地方,它帮助我们逐步找到最小值。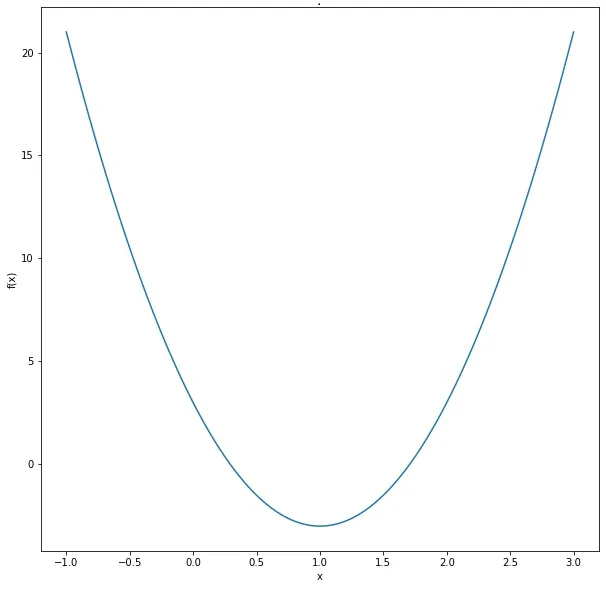
在梯度下降中,我们计算梯度,对于一维问题来说,梯度本质上是它的一阶导数。在我们的例子中,导数 d/dx = 12x – 12。然后,我们初始化 x 为一个随机值,并计算函数的输出。通过计算 x 的梯度,我们得到斜率方向。
我们将 x 按梯度的相反方向调整一个小的量。步长通常被称为学习率,这是为了避免超调而错过最小值。在数学文献和编程库中,通常会看到希腊字母 η 或 eta 作为学习率的参数。梯度下降算法的更新规则为 x <- x – η * d/dx。
假设我们将 x 初始化为 -0.9,并将学习率 eta 设置为 0.03。在第一步中,梯度将为 12 * (-0.9) – 12 = -22.8。x 的第一个更新将为 x <- -0.9 – 0.03 * (-22.8),这给出了 -0.216。现在我们离最小值 1 更近了。
接下来的更新将依次为:
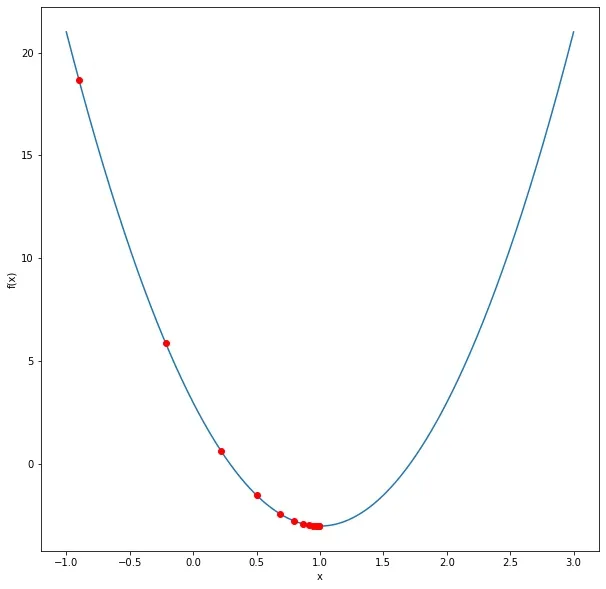
随着我们继续迭代,x 最终会接近 1。如你所见,随着我们接近最小值,变化变得更小,因为斜率变得更平缓。
在这个简单的一维示例中,这个过程似乎很直观。然而,在实际的机器学习问题中,我们通常处理高维数据和具有数癃万参数的复杂模型。尽管存在这种复杂性,但原则仍然保持不变:迭代地将参数调整到下降的方向,直到达到最小值。
这就是梯度下降的威力所在。它为训练复杂的机器学习模型提供了一种实用的可扩展方法,即使底层的数学函数过于复杂而无法解析求解。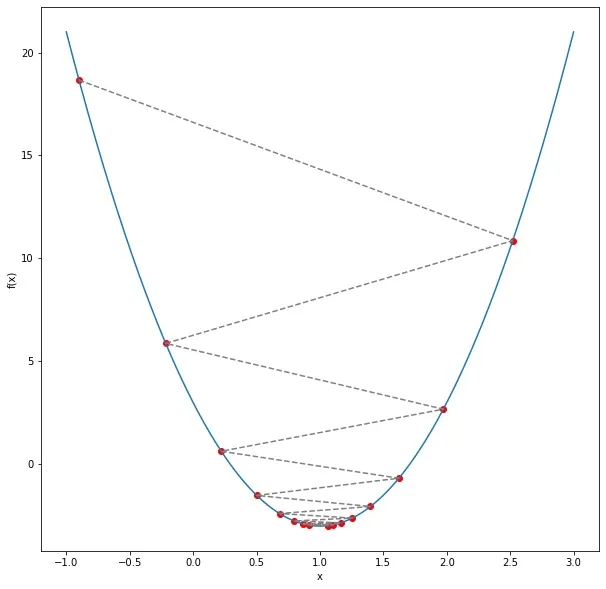
在实际应用中,机器学习模型,尤其是深度学习模型,通常具有许多维度。每个维度对应于模型用来进行预测的不同参数或特征。尽管增加了复杂性,但梯度下降的原则与上面所解释的相同。主要区别在于我们现在需要分别计算每个参数的偏导数。
考虑一个二维函数 f(x,y) = 6x^2 + 9y^2 – 12x – 14y + 3。这个函数代表了一个具有两个参数 x 和 y 的模型。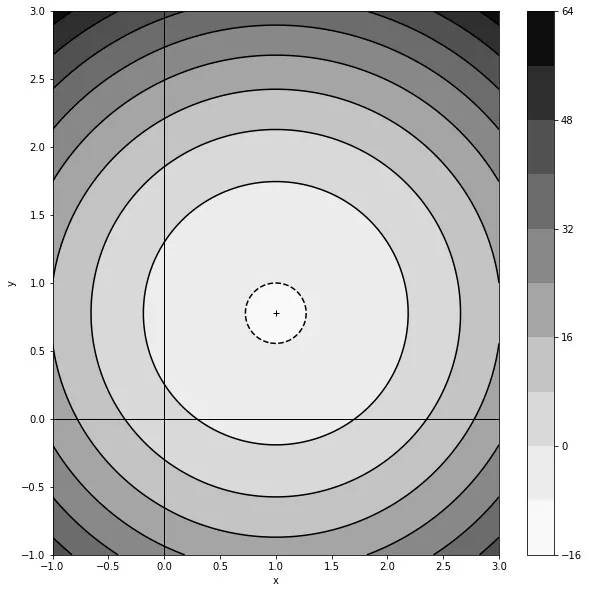
这个函数的梯度是以下偏导数的向量:
这些偏导数告诉我们函数相对于每个参数的斜率。在梯度下降的每一步中,我们需要按照以下方式更新 x 和 y:
通过这种方式,我们根据相应的偏导数调整每个参数的值,朝着能够最大程度减小函数值的方向前进。
在下面的图表中,用等高线和阴影区域表示了函数的景观,浅色区域代表最小值。我们展示了三个不同初始点的梯度下降轨迹。如您所见,无论 x 和 y 的初始值如何,它们在经过几次迭代后最终都会达到最小值。这展示了梯度下降的威力:即使在高维空间中,它也可以指导我们朝着复杂函数的最小值前进。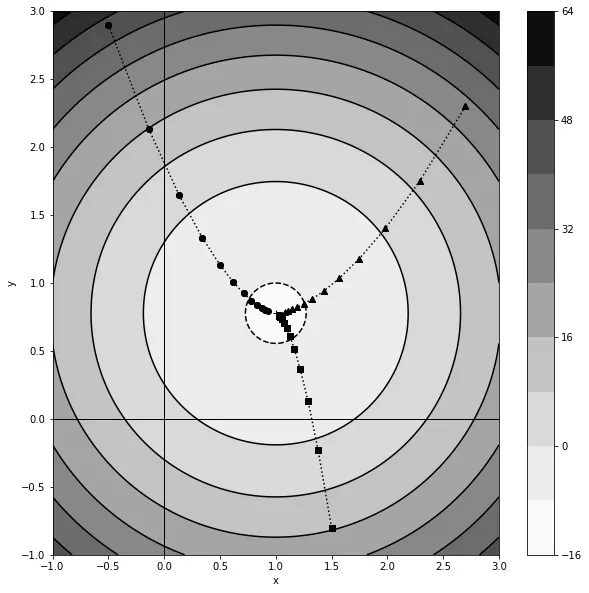
在深度学习中,由于参数的层级和相互连接的性质,获得梯度要复杂得多,并且网络中引入了非线性。这是通过一种称为反向传播的过程来实现的,它使用链式法则来计算人工神经元多个层次上的偏导数。反向传播是训练深度学习模型的关键部分,但它是一个复杂的主题,值得单独一篇文章来详细讨论。关于反向传播的全面解释,推荐阅读《深度学习数学》的第10章。
具有多个极小值的梯度下降 在大多数实际问题中,函数景观不只有一个最优极小值。相反,它有多个极小值,每个极小值代表一个潜在的解释。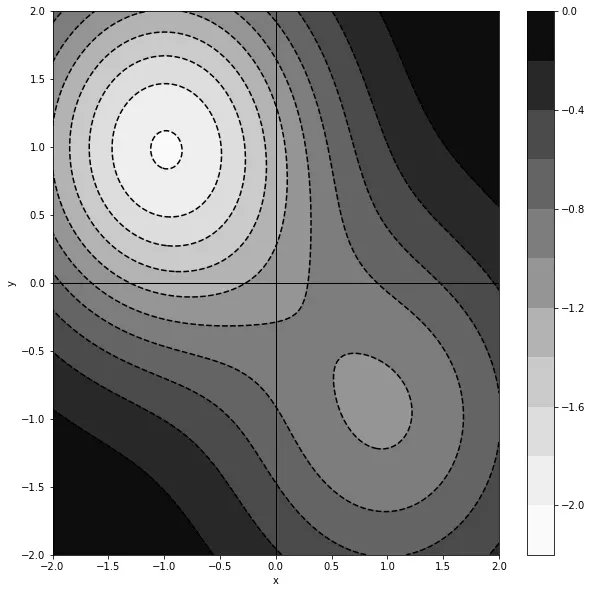
然而,通向这个最优解的路径并不总是直接的。根据参数的初始位置不同,模型可能会收敛到两个极小值之一。这是因为梯度下降法从初始点沿着最陡峭的路径向下前进,但不一定会导向全局最小值。
在理想的情况下,我们会事先了解损失函数的形式,从而能够选择一个良好的初始化点,直接引导我们到全局最小值。然而,在实际情况下,这种情况很少发生。损失函数的形式通常是未知的,因此无法预测最佳的起始点。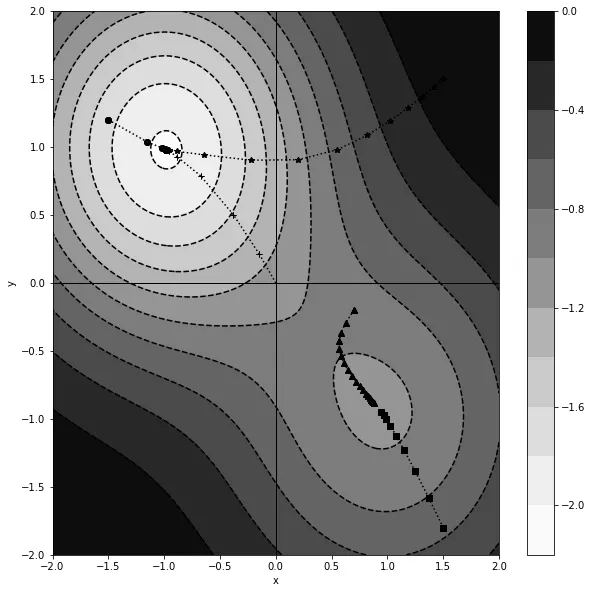
在具有数百万参数的高维问题中,通常存在许多局部最小值,它们的质量相同。这是问题高维性质的结果,增加了找到许多质量几乎相同的解的可能性。
在这种情况下,梯度下降法最终会收敛到许多同样好的局部最小值之一。
在现实世界的深度学习应用中,通常我们会首先创建一个带有标注训练样例的数据集,例如一系列带有对应标签(良性或恶性)的X光影像。
训练模型的过程涉及将每个样例通过模型,进行预测,并计算损失函数。在处理完整个训练集后,我们计算整个样本的损失(例如使用均方误差),然后使用梯度下降法调整模型的参数。当你使用整个数据集计算损失函数的梯度时,这被称为批量梯度下降法。
随着模型和数据集的扩大,执行批量梯度下降法的内存和计算成本变得禁止。这就是为什么机器学习从业者使用小批量梯度下降法。小批量梯度下降法在训练过程的每一步中,不是使用整个数据集,而是使用一部分样例。
通过选择一个随机样本,我们可以得到真实梯度的估计。小批量梯度下降法也被称为随机梯度下降法(SGD)。术语“随机”指的是使用数据集的一部分引入的随机性。
在实践中,随机梯度下降法通常优于批量梯度下降法。其原因是多个小批量引入的随机性使得模型能够更好地概括底层分布,而不是过拟合整个数据集。这种随机性有助于模型逃离浅层局部最小值,并找到更好的整体解。
对于小批量中样本数量的选择,没有固定的规则。最佳的小批量大小可能取决于各种因素,包括问题的性质、数据集的大小和模型的复杂性。通常需要通过试验不断调整,这也是机器学习从业者在调整模型以获得最佳性能时花费大量时间的超参数之一。
本文简要介绍了梯度下降法。重要的是要注意,这只是冰山一角。远远超出了我们所涵盖的内容,还有大量的知识等待我们去发现。
我们忽略了梯度下降法中的动量技术。这一技术受到物理学的启发,帮助算法更高效地在参数空间中导航。除了基本的梯度下降法,还有几种其他变种算法值得探索。这些包括RMSprop、Adagrad和Adam,每种算法都具有独特的优势和应用场景。
如果想深入了解这些主题和更多内容,可以阅读Ronald T. Kneusel的《深度学习数学》。这本全面的指南将为您打下坚实的基础,让您具备解决深度学习领域更复杂问题的知识能力。
来源:https://bdtechtalks.com/2023/07/31/what-is-gradient-descent/

深度学习模型以各种形式存在,每种形式都针对特定任务进行了定制。从密集层到卷积神经网络(CNN),循环神经网络(RNN),以及更近期的transformer,深度学习的领域是多样且引人入胜的。然而,在这种多样性背后存在着一条将这些模型联系在一起的共同线索-梯度下降的原则,即训练机器学习模型的技术。
深度学习的数学基础常常令人望而却步。Ronald T. Kneusel的《深度学习数学》,深入探讨了深度学习的数学复杂性,并通过示例、Python代码和图示来使其易于理解。
在本文中,我们将试图揭秘梯度下降,而不深入探讨数学细节。本文汲取了《深度学习数学》第11章的灵感,该章全面解释了梯度下降。对于更深入的理解,强烈推荐阅读整本书。它是对深度学习数学感兴趣的任何人的宝贵资源。
梯度下降是什么?
梯度下降背后的一般思想是通过迭代调整机器学习模型的参数,以最小化其错误。错误通过损失函数计算,损失函数计算模型预测值与实际值之间的差异,也被称为基准真值。换句话说,梯度下降的目标是找到损失函数的最小值。
梯度下降的基本思想是通过迭代地调整机器学习模型的参数,以最小化其错误。错误是通过损失函数计算得出的,它计算模型预测值与实际值(也称为基准真值)之间的差异。换句话说,梯度下降的目标是找到损失函数的最小值。
为了理解梯度下降的工作原理,想象一下你正盲目地尝试找到山谷中的最低点。你可以感受到脚下的坡度,并决定往哪个方向前进。你迈出一步,再次感受坡度,并调整你的方向。
这实质上就是梯度下降的工作方式。它从一个预测开始,计算错误,并根据损失函数的斜率调整模型的参数。通过重复这个过程,模型学习逼近基础数据的分布。
梯度下降中的“梯度”是指损失函数相对于模型参数的斜率。由于我们想要最小化误差,所以我们沿着斜率的相反方向前进,因此称之为“下降”。
一维梯度下降
为了理解梯度下降的工作原理,让我们考虑一个简单的一维问题。假设我们有一个具有单个参数x的机器学习模型。我们的目标是找到最小化损失函数的x的值,损失函数计算模型的预测值与实际值之间的误差。
假设数据的基础函数是f(x) = 6x^2 – 12x + 3。理论上,我们可以通过将一阶导数设置为零并解出x来找到函数的最小值。然而,在现实世界的应用中,问题往往非常复杂,我们事先不知道函数的形式,无法通过解析的方法来求解。这就是梯度下降发挥作用的地方,它帮助我们逐步找到最小值。

一个简单的一维函数
在梯度下降中,我们计算梯度,对于一维问题来说,梯度本质上是它的一阶导数。在我们的例子中,导数 d/dx = 12x – 12。然后,我们初始化 x 为一个随机值,并计算函数的输出。通过计算 x 的梯度,我们得到斜率方向。
我们将 x 按梯度的相反方向调整一个小的量。步长通常被称为学习率,这是为了避免超调而错过最小值。在数学文献和编程库中,通常会看到希腊字母 η 或 eta 作为学习率的参数。梯度下降算法的更新规则为 x <- x – η * d/dx。
假设我们将 x 初始化为 -0.9,并将学习率 eta 设置为 0.03。在第一步中,梯度将为 12 * (-0.9) – 12 = -22.8。x 的第一个更新将为 x <- -0.9 – 0.03 * (-22.8),这给出了 -0.216。现在我们离最小值 1 更近了。
接下来的更新将依次为:
0.2217
0.5019
0.68120.7959
0.8694

一个简单的一维函数
随着我们继续迭代,x 最终会接近 1。如你所见,随着我们接近最小值,变化变得更小,因为斜率变得更平缓。
在这个简单的一维示例中,这个过程似乎很直观。然而,在实际的机器学习问题中,我们通常处理高维数据和具有数癃万参数的复杂模型。尽管存在这种复杂性,但原则仍然保持不变:迭代地将参数调整到下降的方向,直到达到最小值。
这就是梯度下降的威力所在。它为训练复杂的机器学习模型提供了一种实用的可扩展方法,即使底层的数学函数过于复杂而无法解析求解。

多维梯度下降
在实际应用中,机器学习模型,尤其是深度学习模型,通常具有许多维度。每个维度对应于模型用来进行预测的不同参数或特征。尽管增加了复杂性,但梯度下降的原则与上面所解释的相同。主要区别在于我们现在需要分别计算每个参数的偏导数。
考虑一个二维函数 f(x,y) = 6x^2 + 9y^2 – 12x – 14y + 3。这个函数代表了一个具有两个参数 x 和 y 的模型。

具有单个最小值的简单二维函数
这个函数的梯度是以下偏导数的向量:
d/dx = 12x – 12
d/dy = 18y – 14
这些偏导数告诉我们函数相对于每个参数的斜率。在梯度下降的每一步中,我们需要按照以下方式更新 x 和 y:
x <- x – η * d/dx
y <- y – η * d/dy
通过这种方式,我们根据相应的偏导数调整每个参数的值,朝着能够最大程度减小函数值的方向前进。
在下面的图表中,用等高线和阴影区域表示了函数的景观,浅色区域代表最小值。我们展示了三个不同初始点的梯度下降轨迹。如您所见,无论 x 和 y 的初始值如何,它们在经过几次迭代后最终都会达到最小值。这展示了梯度下降的威力:即使在高维空间中,它也可以指导我们朝着复杂函数的最小值前进。

具有单个最小值的二维函数上的梯度下降。
在深度学习中,由于参数的层级和相互连接的性质,获得梯度要复杂得多,并且网络中引入了非线性。这是通过一种称为反向传播的过程来实现的,它使用链式法则来计算人工神经元多个层次上的偏导数。反向传播是训练深度学习模型的关键部分,但它是一个复杂的主题,值得单独一篇文章来详细讨论。关于反向传播的全面解释,推荐阅读《深度学习数学》的第10章。
具有多个极小值的梯度下降 在大多数实际问题中,函数景观不只有一个最优极小值。相反,它有多个极小值,每个极小值代表一个潜在的解释。

具有多个最小值的二维函数。
然而,通向这个最优解的路径并不总是直接的。根据参数的初始位置不同,模型可能会收敛到两个极小值之一。这是因为梯度下降法从初始点沿着最陡峭的路径向下前进,但不一定会导向全局最小值。
在理想的情况下,我们会事先了解损失函数的形式,从而能够选择一个良好的初始化点,直接引导我们到全局最小值。然而,在实际情况下,这种情况很少发生。损失函数的形式通常是未知的,因此无法预测最佳的起始点。

具有多个最小值的函数的梯度下降。
在具有数百万参数的高维问题中,通常存在许多局部最小值,它们的质量相同。这是问题高维性质的结果,增加了找到许多质量几乎相同的解的可能性。
在这种情况下,梯度下降法最终会收敛到许多同样好的局部最小值之一。
随机梯度下降法
在现实世界的深度学习应用中,通常我们会首先创建一个带有标注训练样例的数据集,例如一系列带有对应标签(良性或恶性)的X光影像。
训练模型的过程涉及将每个样例通过模型,进行预测,并计算损失函数。在处理完整个训练集后,我们计算整个样本的损失(例如使用均方误差),然后使用梯度下降法调整模型的参数。当你使用整个数据集计算损失函数的梯度时,这被称为批量梯度下降法。
随着模型和数据集的扩大,执行批量梯度下降法的内存和计算成本变得禁止。这就是为什么机器学习从业者使用小批量梯度下降法。小批量梯度下降法在训练过程的每一步中,不是使用整个数据集,而是使用一部分样例。
通过选择一个随机样本,我们可以得到真实梯度的估计。小批量梯度下降法也被称为随机梯度下降法(SGD)。术语“随机”指的是使用数据集的一部分引入的随机性。
在实践中,随机梯度下降法通常优于批量梯度下降法。其原因是多个小批量引入的随机性使得模型能够更好地概括底层分布,而不是过拟合整个数据集。这种随机性有助于模型逃离浅层局部最小值,并找到更好的整体解。
对于小批量中样本数量的选择,没有固定的规则。最佳的小批量大小可能取决于各种因素,包括问题的性质、数据集的大小和模型的复杂性。通常需要通过试验不断调整,这也是机器学习从业者在调整模型以获得最佳性能时花费大量时间的超参数之一。
进一步阅读
本文简要介绍了梯度下降法。重要的是要注意,这只是冰山一角。远远超出了我们所涵盖的内容,还有大量的知识等待我们去发现。
我们忽略了梯度下降法中的动量技术。这一技术受到物理学的启发,帮助算法更高效地在参数空间中导航。除了基本的梯度下降法,还有几种其他变种算法值得探索。这些包括RMSprop、Adagrad和Adam,每种算法都具有独特的优势和应用场景。
如果想深入了解这些主题和更多内容,可以阅读Ronald T. Kneusel的《深度学习数学》。这本全面的指南将为您打下坚实的基础,让您具备解决深度学习领域更复杂问题的知识能力。
来源:https://bdtechtalks.com/2023/07/31/what-is-gradient-descent/

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























