混合量子经典算法加速高维时间序列分析的动态模式分解
为了降低广泛使用的动态模式分解算法所需的计算能力,郭国平领导的中国研究小组开发了一种量子经典混合算法。他们在三种应用场景中测试了他们的算法:数据去噪、场景背景提取和流体动力学分析。他们确定它可以只使用少量样本,并且在分析高维时间序列方面具有量子优势。
他们的研究发表在《智能计算》上。
为了加速高维时间序列分析,开发并测试了量子动态模式分解算法。它通过降低对时间序列数据执行的操作的复杂性来实现指数加速。在目前的形式下,它也可以用来加速对某些其他类型数据集的分析。此外,研究人员计划为他们的算法创建新的变体,专门用于其他动态模式分解应用,如库普曼分析。
量子算法的主要限制是样本数量必须保持小,否则不会降低算法的复杂度,并失去量子优势。研究人员在设计算法时充分意识到这一点,因此规定了样本数量的上限,以确保强大的性能。
不过,合肥国家综合科学中心人工智能研究所的研究员程雪解释说:“通过数值测试,我们发现分析特定时间序列所需的样本数量低于我们推导的界限,这进一步说明了我们算法的加速性能。”
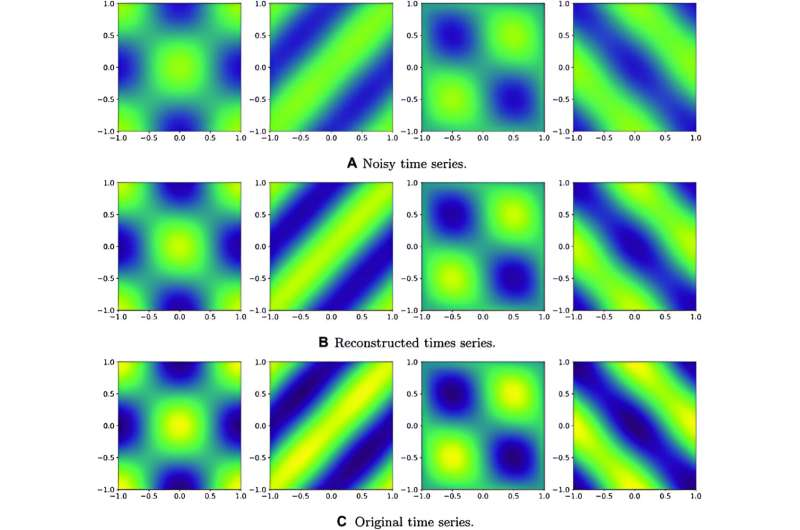
为了测试改变样本数量的效果,研究人员探索了他们的量子算法在不同领域的应用。首先,数据去噪,是一个类似于从图像中去除噪声的过程。第二,场景背景提取,是计算机视觉中常见的任务。它是一种通过比较同一场景的一系列图像来去除前景项目的图像处理方法。第三,流体动力学分析,用于预测气体或液体的运动。该算法成功地执行了这些任务。
在许多可能的应用中,流体动力学尤为重要。“动态模态分解最初用于流场数据分析,”解释说。流体动力学的研究经常产生高维的流场数据,数据维数达到数十亿量级。从这些数据中提取有意义的流场特征是一个具有挑战性的问题。”
动态模态分解算法是时间序列分析中常用的因式分解和降维方法。时间序列分析是对时间序列进行数学或统计运算以发现重要信息的过程。
时间序列是作为一组以时间间隔均匀的一系列样本收集的数据,例如一个月每个交易日结束时的股票指数值,或者一个城市一年中每天的平均温度。
由于高维时间序列在每次采样时由多段信息组成,而不是只有一条信息,因此对高维时间序列的处理和分析计算量更大。时间序列分析广泛应用于经济、金融和各种科学与工程领域。
由于量子计算机仍处于发展阶段,相对难以接近,量子算法方面的工作由“理论推导加数值模拟”组成,但他表示,量子芯片技术正在与量子算法“协同”关系中迅速发展,量子算法有望在“不久的将来”实现“革命性突破”。
量子计算机的能力来源于两个不直观的特性,即叠加和纠缠,这使得它们能够并行执行许多计算。然而,量子计算“只能加快特定问题的速度,并不能取代经典计算机。”































