这个故事探讨了自动分化，这是现代深度学习框架的一个特征，它在训练循环中自动计算参数梯度。本文结合使用Python和c++的实际示例介绍了这种技术。

路线图

1. 自动微分：是什么，动机等

2. Python中使用TensorFlow的自动微分

3. c++中的Eigen自动微分

4. 结论

自动微分

PyTorch或TensorFlow等现代框架有一个增强的功能，称为自动微分，或者简称为autodiff。顾名思义，autodiff自动计算函数的导数，减少了开发人员自己实现这些导数的责任。

autodiff的相关性是什么?

现在每个深度学习框架都使用autodiff来计算可训练参数的梯度。

在autodiff广泛使用之前，开发模型的大部分时间都花在实现计算梯度的代码上(或者实际上调试或删除梯度代码中的错误)。

因此，autodiff是深度学习普及的游戏规则改变者。它允许即使没有扎实微积分技能的开发人员也可以自信地实现复杂的机器学习算法。即使对于具有丰富微积分知识的开发人员，autodiff也很有帮助，因为它减少了出现错误或次优实现的机会。

为什么理解autodiff很重要?

在机器学习中，autodiff完全抽象了梯度计算，通常提供异常准确和快速的计算，而无需模型开发人员的任何努力。通常。但并非总是如此。

由于数字不稳定等因素，autodiff在极少数情况下可能会失败。因此，了解autodiff的工作原理可以帮助你做好准备:(i)尽可能多地使用autodiff， (ii)检测autodiff何时失败，以及(iii)在必要时修复它。

值得注意的是，在反向传播中，梯度的计算是比较关键和昂贵的部分，完全由autodiff完成。因此，理解autodiff完全是必须的。

使用TensorFlow自动微分

如果你使用Google TensorFlow，你可能从来没有想过自己派生一个层。让我们从一个简单的例子开始:

import tensorflow as tf
class CustomLayer(tf.keras.layers.Layer):
  def __init__(self, num_outputs, activation):
    super(CustomLayer, self).__init__()
    self.num_outputs = num_outputs
    self.activation = activation
  def build(self, input_shape):
    self.kernel = self.add_weight("kernel",
                                  shape=[int(input_shape[-1]),
                                         self.num_outputs])
  def call(self, inputs):
    Z = tf.matmul(inputs, self.kernel)
    Y = self.activation(Z)
    return Y

这个自定义层基本上是tf.keras.layers. dense的克隆，没有任何偏差。我们可以这样使用它:

def sin_activation(x):
    return tf.sin(x)
my_custom_layer = CustomLayer(2, sin_activation)
input = tf.constant([[-1., 0., 1.], [2., 3., 4.], [-1., -5., 2.]])
with tf.GradientTape() as tape:
    output = my_custom_layer(input)
    loss = tf.reduce_sum(output**2)
gradient = tape.gradient(loss, my_custom_layer.trainable_variables)
print("my_custom_layer.trainable_variables:\n", my_custom_layer.trainable_variables[0].numpy())
print("\ngradient:\n", gradient[0].numpy())

这段代码输出如下:

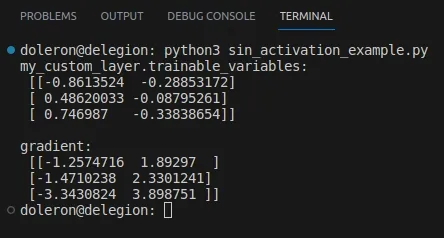
由于我们没有使用内置的激活函数(如tf.keras.activation.relu)， TensorFlow如何知道如何计算该梯度？答案很简单：使用自动微分。

autodiff是如何工作的

TensorFlow没有要求开发人员提供sin_activation的显式导数，而是使用autodiff计算梯度。但是autodiff是如何工作的呢?

也许你已经上了很长时间的微积分课，学习如何使用微分规则计算函数的导数。autodiff用同样的规则求导数吗?是的，但和你做的不一样。

autodiff的中心思想是将计算图分解为导数简单且已知的初等运算，然后递归应用链式法则计算最上面的导数。

例如，让我们看看在最后一个例子中损失是如何计算的:

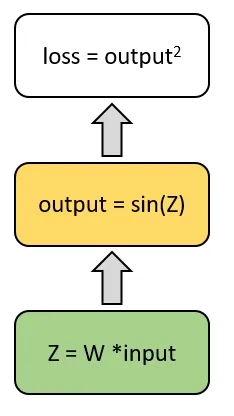
该图描述了损失值的计算流程。利用链式法则，我们可以得到损失梯度关于权值的公式:

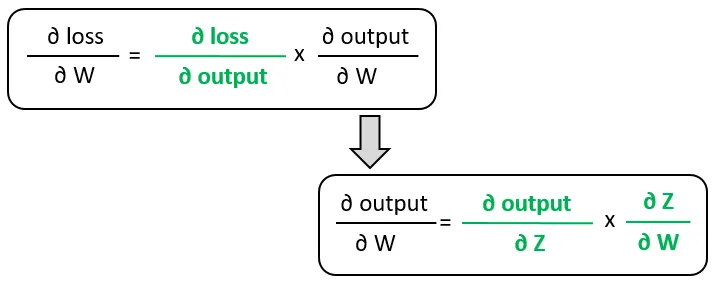
可以简化为:

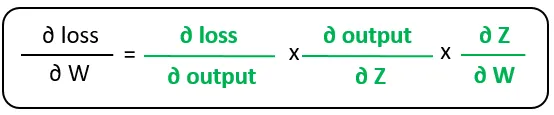
注意，最右边的偏导数是梯度计算图的叶子。它们在某种程度上是初等的，这意味着我们不能从它们推导出任何其他的导数。

现在，autodiff需要找到这些叶子梯度的值，这可以通过使用基本的微积分规则来简单地解决:

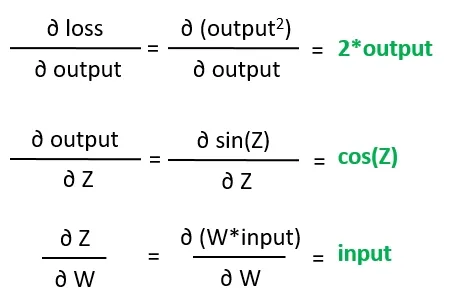
最后，通过以下计算得到损失相对于权重的梯度:

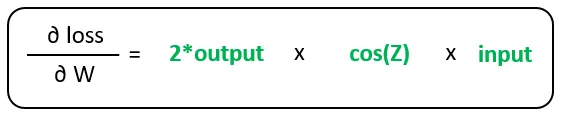
Autodiff在木材下执行此图计算，而不需要开发人员的显式干扰。

数值不稳定性开始发挥作用

正如本故事的第一部分所述，在某些情况下，由于中间梯度或叶片梯度的数值不稳定，autodiff失败。考虑下面的例子:

import tensorflow as tf
input = tf.Variable(100.0)
def function_using_autodiff(x):
    return 1./tf.exp(x)
with tf.GradientTape() as tape:
    output = function_using_autodiff(input)
gradient = tape.gradient(output, input)
print("output using autodiff: ", output.numpy())
print("gradient using autodiff: ", gradient.numpy())

该程序输出:

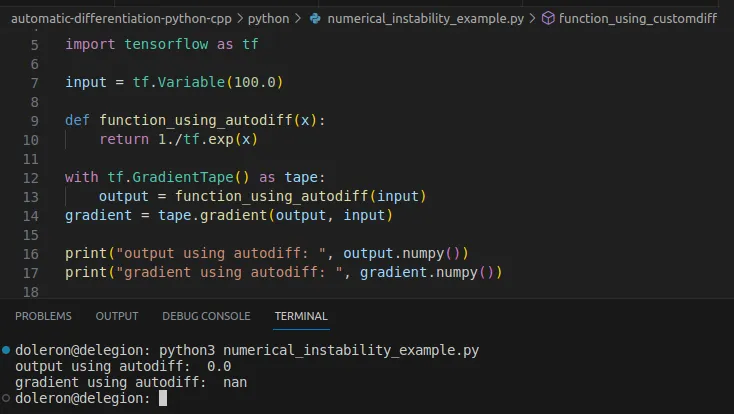
在本例中，虽然函数在x=100处被正确地求值，但autodiff提供的梯度是nan。让我们通过使用自定义渐变来解决这个问题。首先，让我们检查函数表达式:

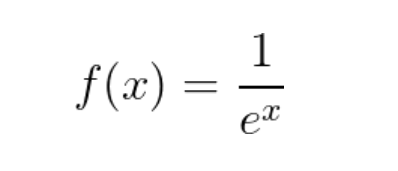
该函数的导数为:

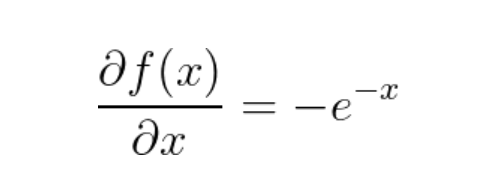
现在，我们可以实现这个导数作为自定义梯度如下:

import tensorflow as tf
@tf.custom_gradient
def function_using_customdiff(x):
    e = tf.exp(x)
    def grad(upstream):
        return upstream * -tf.exp(-x)
    return 1./tf.exp(x), grad
with tf.GradientTape() as tape:
    output = function_using_customdiff(input)
gradient = tape.gradient(output, input)
print("output using custom diff: ", output.numpy())
print("gradient using custom diff: ", gradient.numpy())

这次，对梯度进行了正确的评估:

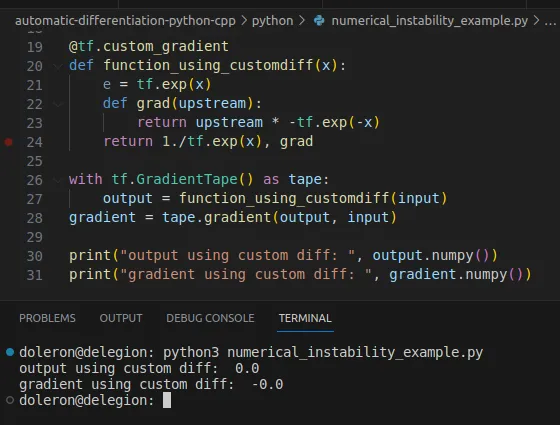
有时，数值不稳定性来自于手边函数的理论性质。例如，下面这个函数的导数：

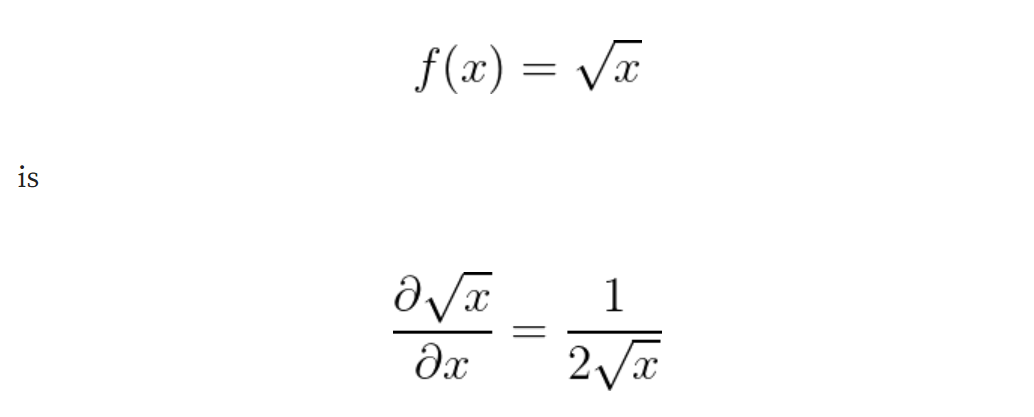
当x = 0时，它显然没有定义，即使f(0) = 0，我们还可以使用自定义梯度来为这种情况提供方便的(工程)解决方案。

现在我们了解了如何在Python/TensorFlow中使用autodiff，让我们学习如何在c++程序中使用该技术。

在c++中使用Eigen与autodiff

Eigen是迄今为止最成功的c++高性能代数库之一。

使用特征Autodiff[5]非常简单。让我们从一个简单但具有说明性的例子开始。考虑下面的函数:

template<typename T>
T my_function(const T& x)
{
    T result = T(1)/(T(1) + exp(-x));
    return result;
}

注意，我们将这个函数定义为模板函数。不深入细节，模板函数是函数的模具。不是函数，真的。这样的模板很有用，因为我们可以用不同的数据类型重用my_function。

通常，我们会使用float、double或int等类型调用函数。然而，为了使Eigen Autodiff工作，我们必须以Eigen::AutoDiffScalar的形式传递值。看看下面的例子:

#include <iostream>
#include <unsupported/Eigen/AutoDiff>
int main(int, char **)
{
    Eigen::AutoDiffScalar<Eigen::VectorXd> X;
    X.derivatives() = Eigen::VectorXd::Unit(1, 0);
    X.value() = 2.f;
    auto Y = my_function(X);
    std::cout << "Y: " << Y << "\n\n";
    std::cout << "derivatives:\n" << Y.derivatives() << "\n";
    return 0;
}

这里的第一点是头部不支持/Eigen/AutoDiff。在这个文件中，Eigen定义了类型Eigen::AutoDiffScalar，用于输入变量x。再次检查下面两行:

X.derivatives() = Eigen::VectorXd::Unit(1, 0);
X.value() = 2.f;

这些行设置X的值及其索引。因为X是这个例子中唯一的变量，所以它的索引是0。

现在，我们可以像往常一样将X传递给my_function:

auto Y = my_function(X);

Y也是一个特征::AutoDiffScalar。正如我们在代码中看到的，y的每个偏导数的值都存储在derivatives()数组中。运行这段代码会得到以下输出:

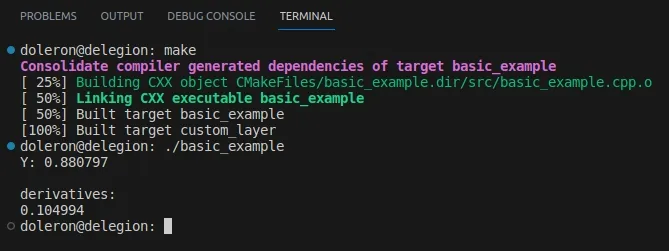
Y存储了函数的输出值和对x的导数，我们怎么知道这些值是否正确?你可能会注意到my_function实际上是sigmoid公式:

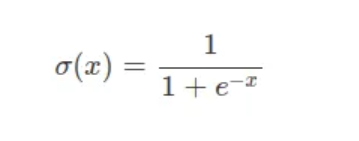
众所周知，sigmoid导数公式为:

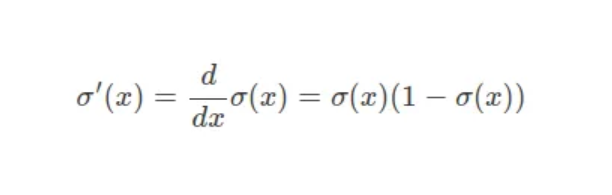
因此，一个简单的计算器可以重复检查σ(2) = 0.8808和σ '(2) = 0.10499的值。

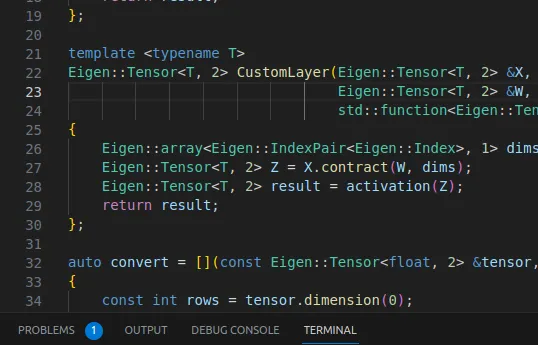
使用c++和Eigen实现CustomLayer

一旦我们知道了如何在c++中使用autodiff和Eigen，我们就可以重写CustomLayer的例子了，这次是用c++:

#include <unsupported/Eigen/CXX11/Tensor>
template <typename T>
Eigen::Tensor<T, 2> CustomLayer(Eigen::Tensor<T, 2> &X, Eigen::Tensor<T, 2> &W, std::function<Eigen::Tensor<T, 2>(Eigen::Tensor<T, 2>&)> activation)
{
    Eigen::array<Eigen::IndexPair<Eigen::Index>, 1> dims = { Eigen::IndexPair<Eigen::Index>(1, 0) };
    Eigen::Tensor<T, 2> Z = X.contract(W, dims);
    Eigen::Tensor<T, 2> result = activation(Z);
    return result;
};

在此，强调三点:

1. 我们用的是特征张量而不是特征矩阵。

2. 我们正在进行压缩。压缩是矩阵乘积的多维推广。

3. 我们正在使用一个模板函数。模板类也可以。这里的重点是将其定义为模板，就像我们在前面的示例中所做的那样。

此外，我们将激活作为std::函数传递。现在让我们来定义一下:

template <typename T>
T sine(T t) {
    return sin(t);
}
template <typename T>
Eigen::Tensor<T, 2> sin_activation(Eigen::Tensor<T, 2> & P) {
    Eigen::Tensor<T, 2> result = P.unaryExpr(std::ref(sine<T>));
    return result;
};

同样，我们使用的是模板。这里的一切都很简单。我们只是用unaryExpr用sint函数映射P。现在，我们终于可以调用CustomLayer了:

#include <unsupported/Eigen/AutoDiff>
typedef typename Eigen::AutoDiffScalar<Eigen::VectorXf> AutoDiff_T;
int main(int, char **)
{
    Eigen::Tensor<float, 2> x_in(3, 3);
    x_in.setValues({{-1., 0., 1.}, {2., 3., 4.}, {-1., -5., 2.}});
    Eigen::Tensor<float, 2> w_in(3, 2);
    w_in.setRandom();
    Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in);
    Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, 0, w_in.size());
    auto Y = CustomLayer(X, W, sin_activation<AutoDiff_T>);
    auto output = Y * Y;
    auto LOSS = ((Eigen::Tensor<AutoDiff_T, 0>)output.sum())(0);
    auto dY_dW = gradients(LOSS, W);
    std::cout << "trainable_variables:\n" << W << "\n\n";
    std::cout << "gradient:\n" << dY_dW << "\n\n";
    std::cout << "output:\n" << output << "\n\n";
    std::cout << "loss:\n" << LOSS << "\n\n";
    return 0;
}

顾名思义，convert函数将原始规范张量x_in和w_in转换为Eigen::Tensor<AutoDiff_T, 2>张量。正如我们在上一个示例中讨论的那样，Eigen::AutoDiffScalar类型是Eigen:: autodiff工作所必需的。Convert的定义如下:

auto convert = [](const Eigen::Tensor<float, 2> &tensor, int offset = 0, int size = 0)
{
    const int rows = tensor.dimension(0);
    const int cols = tensor.dimension(1);
    Eigen::Tensor<AutoDiff_T, 2> result(rows, cols);
    for (int i = 0; i < rows; ++i)
    {
        for (int j = 0; j < cols; ++j)
        {
            int index = i * cols + j;
            result(i, j).value() = tensor(i, j);
            if (size) {
                result(i, j).derivatives() = Eigen::VectorXf::Unit(size, offset + index);
            }
        }
    }
    return result;
};

注意调用convert时的两行代码:

Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in);
Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, 0, w_in.size());

结果是我们只要求w的偏导数。

在式中，Y是层的输出值和对w的偏导数，然后可以使用梯度函数来解包梯度:

auto gradients(const AutoDiff_T &LOSS, const Eigen::Tensor<AutoDiff_T, 2> &W)
{
    auto derivatives = LOSS.derivatives();
    int index = 0;
    Eigen::Tensor<float, 2> result(W.dimension(0), W.dimension(1));
    for (int i = 0; i < W.dimension(0); ++i)
    {
        for (int j = 0; j < W.dimension(1); ++j)
        {
            float val = derivatives[index];
            result(i, j) = val;
            index++;
        }
    }
    return result;
}

构建并运行它之后，这段代码输出如下所示:

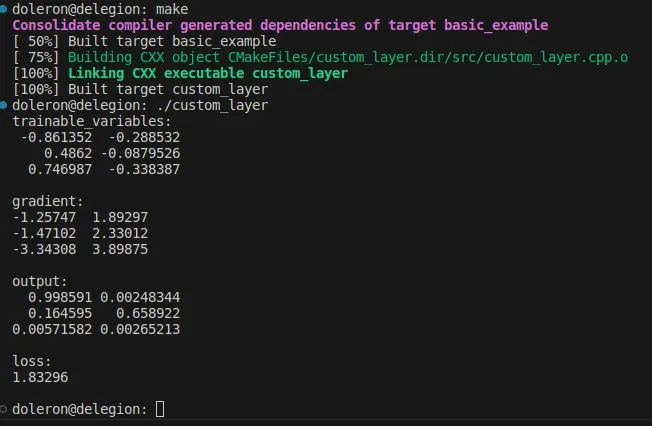
正如预期的那样，输出与Python/TensorFlow示例生成的输出相似。

求关于X的导数

在上一个例子中，我们只计算了w的梯度。如果我们也对计算X的偏导数感兴趣，我们必须实现以下改变:

int size = x_in.size() + w_in.size();
Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in, 0, size);
Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, x_in.size(), size);

这段代码基本上通知了Eigen继续跟踪X的导数。注意，要解压缩xandw，你也必须改变梯度函数:

auto gradients(const AutoDiff_T &Y, const Eigen::Tensor<AutoDiff_T, 2> &X, const Eigen::Tensor<AutoDiff_T, 2> &K)
{
    auto derivatives = Y.derivatives();
    int index = 0;
    Eigen::Tensor<float, 2> dY_dX(X.dimension(0), X.dimension(1));
    for (int i = 0; i < X.dimension(0); ++i)
    {
        for (int j = 0; j < X.dimension(1); ++j)
        {
            float val = derivatives[index];
            dY_dX(i, j) = val;
            index++;
        }
    }
    Eigen::Tensor<float, 2> dY_dK(K.dimension(0), K.dimension(1));
    for (int i = 0; i < K.dimension(0); ++i)
    {
        for (int j = 0; j < K.dimension(1); ++j)
        {
            float val = derivatives[index];
            dY_dK(i, j) = val;
            index++;
        }
    }
    return std::make_pair(dY_dX, dY_dK);
}

现在，你应该相应地调用梯度:

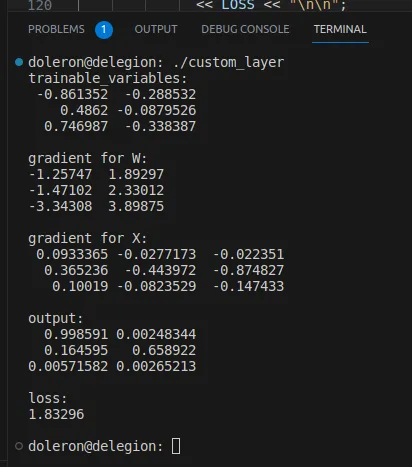
auto [dY_dX, dY_dW] = gradients(LOSS, X, W);

传递X和w后，再次运行程序会得到以下输出:

结论

本文介绍了autodiff，这是深度学习领域最前沿的学科之一。在过去二十年中，在开源包中实现这项技术的成功是人工智能发展和普及的巨大成就。