每个数据科学家都知道这一点：机器学习问题的解决的第一步是对数据进行探索。

这不仅仅是理解哪些特征能帮助你解决问题。实际上，这需要领域知识、大量的努力、大量的询问和尝试寻找答案。这是一个必要的步骤，但在我看来，是第二步。

第一步在某种程度上，取决于对数据复杂性的分析。他们是否要求你在某些事物中找到细节和模式，而这些事物在某种程度上总是相同的，或者输出完全不同？他们要求你找到0.0001和0.0002之间的距离，还是希望你找到0和10之间的距离？

1. 1/0时间序列的熵（理论）

让我们从一个非常简单的例子开始定义熵：一个只能取值为1和0的时间序列。我知道这不完全是我们通常处理的时间序列类型，但你可以想象一下，就好像你每分钟都在你的房间里抛硬币：如果是正面，你测量到1，如果是反面，你测量到0。

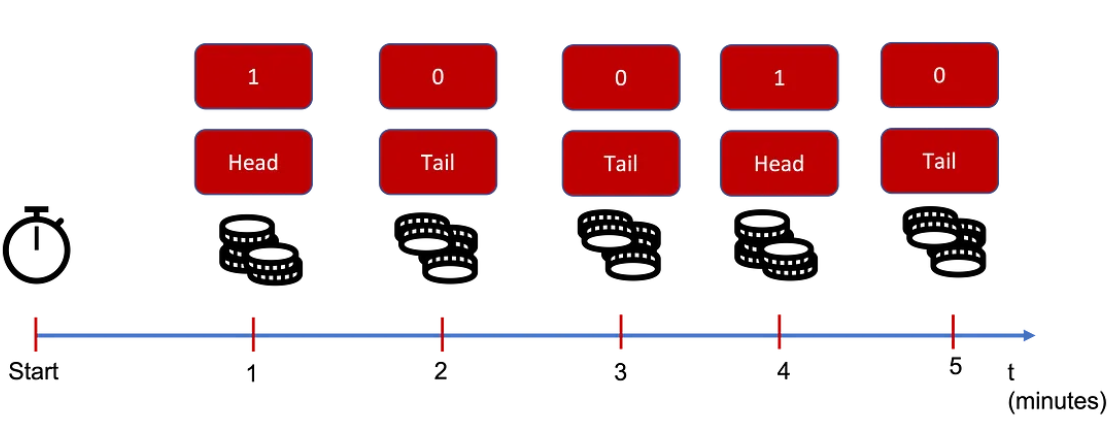
现在，如果你仔细想想，当你不能完全理解某件事时，或者当它不能给你提供大量信息时，它就会变得更“复杂”。

这是熵的方程:

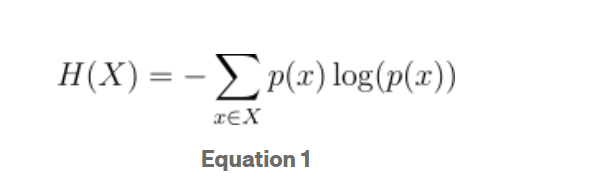
让我们来分析一下:

X是时间序列的定义域，这里X = {0,1}

p(x)是验证x中值x的概率

假设X为0(反面)的概率是0 X为1(正面)的概率是1。这甚至不是一个真正的时间序列，因为它总是1。熵的值是多少?

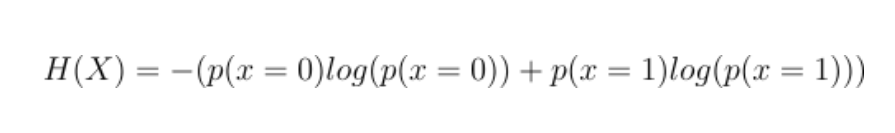
现在p(x=0)=0，所以第一个贡献是0。P (x=1)=1，但1的对数是0。这意味着第二个贡献也是0，而熵确实是0。

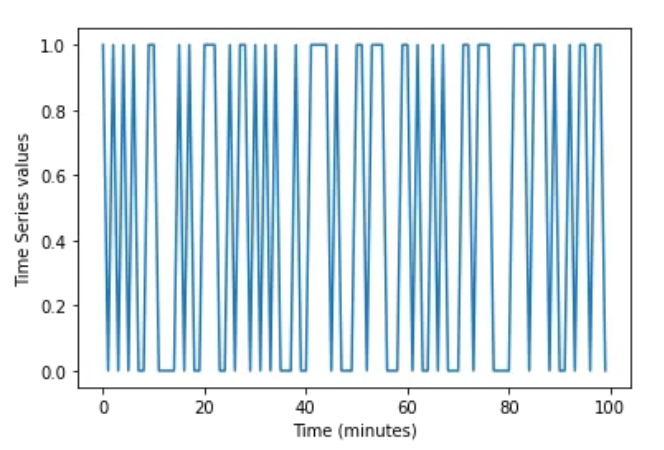
熵等于0是什么意思？时间序列一点也不复杂，因为它看起来是这样：

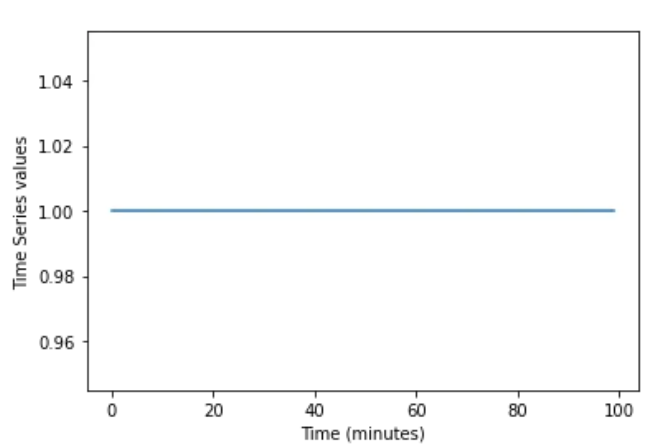
在这个时间序列中没有“复杂性”，这就是为什么它的熵是0。

再举一个同样的例子如果我们知道p(x=0)=p(x=1)=0.5，这意味着出现1和0(正面或反面)的概率是一样的

熵现在变成了:

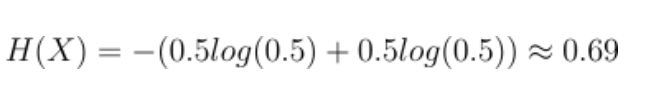
它大于0。这个值本身没有意义，但它是你可以拥有的最大值。这意味着如果你改变p(x=0)使其不等于0.5熵就会降低。

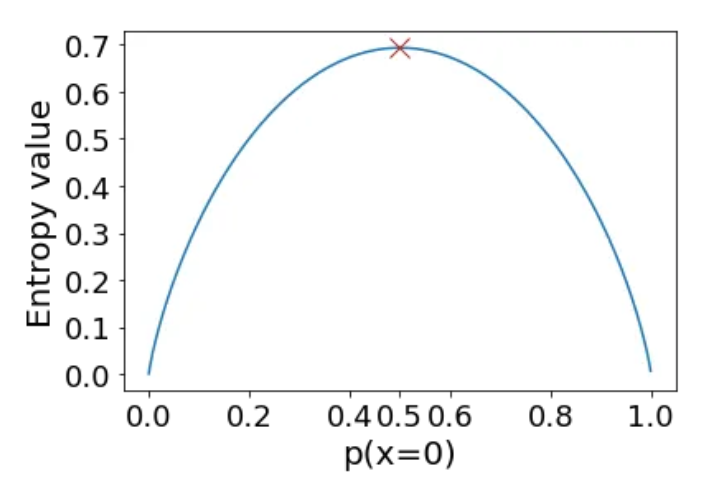
*注意，当你改变p(x=0)时，你也改变p(x=1)为p(x=1)=1-p(x=0)

当概率为0时，这意味着没有复杂性，因为我们已经知道了一切:你有一个值，只有一个值。

当概率是0.0001时，这意味着复杂性很小因为x可能等于0，但大多数情况下x等于1。

当概率为0.5时，现在的复杂性是最大的，因为你真的不知道接下来会发生什么：它可能是1或0，但概率相同。

2. 1/0时间序列的熵(练习)

在我们的代码中，我们将使用Python，我们也将使用非常基本的库:

import numpy as np
import matplotlib.pyplot as plt

让我们编写代码来找到相同的解决方案，但使用“回顾性”的概率，或者如果你愿意，使用它们的频率定义:

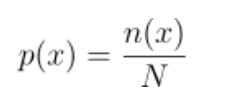
介绍下:

1. X是定义域中的一个值:在本题中，我们只有0和1，所以X要么是0要么是1

2. N (x)是x在时间序列中出现的次数

3. N是时间序列的长度

我们要求出p(x=0)和p(x=1)，然后用上面的方程1…

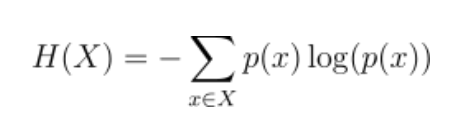
在Python中，你可以用这段非常简单的代码做到这一点:

def entropy_practice(X):
    number_of_values = list(set(X))
    N = len(X)
    p_s = 0
    for x in number_of_values:
        n_x = len(np.where(X==x)[0])
        p_x = n_x/N
        p_s = p_s + p_x*np.log(p_x)
    return -p_s

它有用吗?让我们来测试一下!

让我们生成一个100的长时间序列，其0的概率为0.5:

p_0 = 0.5
X = np.random.choice([0,1],p=[p_0,1-p_0],size=100)
print('The number of 0 in the time series is %i, out of %i'%(len(np.where(X==0)[0]),len(X)))
print('The number of 1 in the time series is %i, out of %i'%(len(np.where(X==1)[0]),len(X)))

The number of 0 in the time series is 53, out of 100
The number of 1 in the time series is 47, out of 100

这样我们有了平衡时间序列。我们设0.5作为概率并不等于50和50，这在估计概率时，会有一些误差。

计算理论熵的公式如下:

def entropy(p):
    return -(p*np.log(p)+(1-p)*np.log(1-p))

让我们看看理论和实际的熵是否匹配:

p_0 = 0.5
X = np.random.choice([0,1],p=[p_0,1-p_0],size=10000)
print('The number of 0 in the time series is %i, out of %i'%(len(np.where(X==0)[0]),len(X)))
print('The number of 1 in the time series is %i, out of %i'%(len(np.where(X==1)[0]),len(X)))
print('The theoretical entropy for p = %.1f is %.2f'%(p_0,entropy(p_0)))
print('The theoretical entropy for p = %.1f is %.2f'%(p_0,entropy_practice(X)))

The number of 0 in the time series is 5010, out of 10000
The number of 1 in the time series is 4990, out of 10000
The theoretical entropy for p = 0.5 is 0.69
The theoretical entropy for p = 0.5 is 0.69

现在让我们改变p_0，看看它们是否匹配:

real_entropies = []
pred_entropies = []
Ps= np.linspace(0.01,0.99,1000)
for p_0 in Ps:
    X = np.random.choice([0,1],p=[p_0,1-p_0],size=1000)
    real_entropies.append(entropy(p_0))
    pred_entropies.append(entropy_practice(X))
plt.plot(Ps, pred_entropies,'.',label='Predicted Entropy',color='navy')
plt.plot(Ps, real_entropies,lw=4,color='darkorange',label='Theoretical Entropy')
plt.legend(fontsize=14)

<matplotlib.legend.Legend at 0x7f31d10aa5e0>

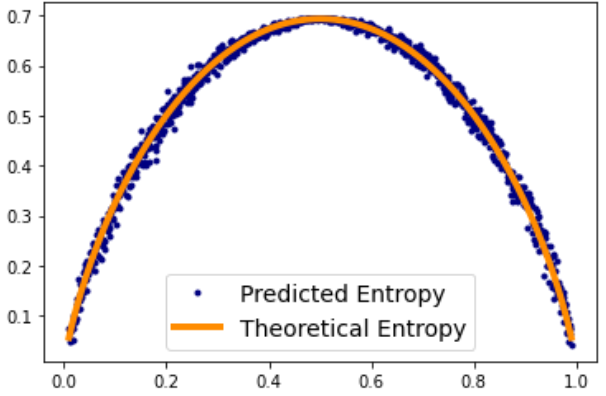
它们匹配的误差很小，对吧?

有趣的是如果我们这样做三次增加时间序列的大小，误差会越来越小

sizes = [100,1000,10000,10**5]
plt.figure(figsize=(16,4))
for i in range(len(sizes)):
    plt.subplot(1,len(sizes),i+1)
    plt.title('Time series size = %i'%(sizes[i]))
    real_entropies = []
    pred_entropies = []
    Ps= np.linspace(0.01,0.99,1000)
    for p_0 in Ps:
        X = np.random.choice([0,1],p=[p_0,1-p_0],size=sizes[i])
        real_entropies.append(entropy(p_0))
        pred_entropies.append(entropy_practice(X))
    plt.plot(Ps, pred_entropies,'.',label='Predicted Entropy',color='navy')
    plt.plot(Ps, real_entropies,lw=4,color='darkorange',label='Theoretical Entropy')
    plt.xlabel('P(X=0)',fontsize=14)
    if i==0:
        plt.ylabel('Entropy',fontsize=14)
    plt.legend(fontsize=12)

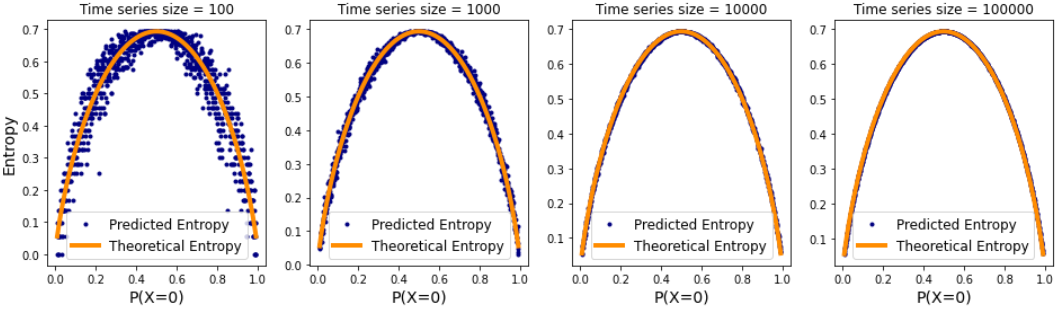
在size = 10k之后，我们的实际熵和预测熵之间的差异基本为0。

3.任意时间序列的熵

现在，如果我们仍然假设我们的时间序列具有离散值(0,1,2，…)，我们可以将熵的定义扩展到不止两个时间序列的值。

例如，让我们选择一个有三个值的情况。所以时间序列可以是0 、1或2。

我们来创建一个新的概率向量p_0,p_1, p_2。要做到这一点，我们将生成3个0到100之间的随机数，并将它们存储在一个向量中，然后将其除以总和:

p_vector = np.random.choice(100,size=3)
p_vector = p_vector/sum(p_vector)
print('The generated probability vector for a 3 case time series is p=', p_vector)

The generated probability vector for a 3 case time series is p= [0.26315789 0.42105263 0.31578947]

我们可以像以前一样应用相同的方程(和相同的代码)来找到真实的和预测的熵。

让我们将熵的定义扩展到实熵的定义中:

def entropy(p_vector):
    p_0 = p_vector[0]*np.log(p_vector[0])
    for p in p_vector[1:]:
        p_0 = p_0 + p*np.log(p)
    return -p_0

这也只适用于0/1的情况:

entropy([0.5,0.5])

0.6931471805599453

正如我们所看到的，理论和预测的熵即使在三个值的情况下也是匹配的:

p_vector = np.random.choice(100,size=3)
p_vector = p_vector/sum(p_vector)
X = np.random.choice([0,1,2],p=p_vector,size=10000)
print('The theoretical entropy for p_0 = %.2f, p_1 = %.2f,p_2 = %.2f, is %.2f'%(p_vector[0],p_vector[1],p_vector[2],entropy(p_vector)))
print('The predicted entropy for p_0 = %.2f, p_1 = %.2f,p_2 = %.2f, is %.2f'%(p_vector[0],p_vector[1],p_vector[2],entropy_practice(X)))

The theoretical entropy for p_0 = 0.55, p_1 = 0.02,p_2 = 0.43, is 0.77
The predicted entropy for p_0 = 0.55, p_1 = 0.02,p_2 = 0.43, is 0.77

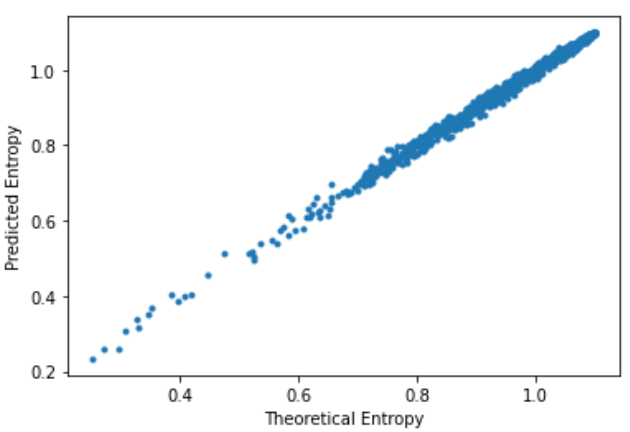
为了向你展示我并没有作弊，我们可以看到这适用于各种情况。如果我们迭代地改变p_vector（和时间序列），我们仍然可以看到真实熵和预测熵相匹配。

real_entropies = []
pred_entropies = []
for i in range(1000):
    p_vector = np.random.choice(100,size=3)
    p_vector = p_vector+1
    p_vector = p_vector/sum(p_vector)
    X = np.random.choice([0,1,2],p=p_vector,size=2000)
    real_entropies.append(entropy(p_vector))
    pred_entropies.append(entropy_practice(X))
plt.plot(real_entropies,pred_entropies,'.')
plt.xlabel('Theoretical Entropy')
plt.ylabel('Predicted Entropy')

Text(0, 0.5, 'Predicted Entropy')

4. 结果

在本文中，我们有哪些结论:

1. 在应用任何机器学习之前，分析时间序列的复杂性

2. 对时间序列的熵和无序的思想进行了反思

3. 定义了熵的数学方程，并举例说明

将其应用于0/1时间序列和0,1,2时间序列的实践中，显示了理论定义如何与我们的计算近似相匹配

现在，这种方法的问题(限制)是，有时时间序列可能太连续，这种方法无法工作。