介绍

在本文中，首先对SVM进行了简要介绍，然后介绍了如何使用量子机器学习（QML）方法针对这种技术进行处理，最后通过使用Titanic数据集的量子增强SVM（QSVM）示例来结束。

SVM和核函数

在这里，我介绍了SVM主要关注分类问题的部分，也就是支持向量分类器（Support Vector Classifier，SVC）。SVC的目标是找到一个最佳边界来将不同类别的数据分开，同时保持最佳的边界间隔。

但是这个将类别进行分隔的边界是什么？假设我们在一个二维向量空间中处理数据，并且有两个类别，如下图所示。

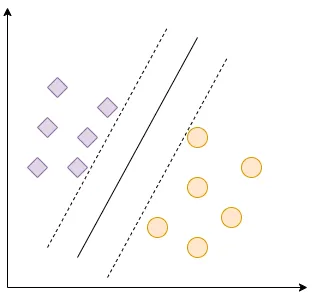
在这个例子中，我们有来自2个不同类别的数据点，我们可以轻松地画出一条分隔两者的线。我们的实线是最佳间隔分隔数据的超平面，如虚线所示。因此，支持向量机尝试找到最佳的分隔器。

如果二维数据看起来像下面的图呢？

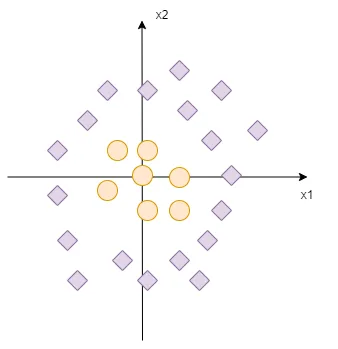
在这种情况下，我们无法正确地划分我们的数据。如果我们看这个图，我们可以画一个圆作为一个很好的分隔器。然而，这个形状既不是一条线也不是一个平面，所以SVM不能直接解决这个问题。然而，这是最酷的SVM技巧，也是高维超平面出现的部分！

如果我们将这些数据转换成更高维的向量空间呢？

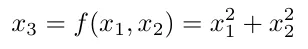
所以我们可以绘制一个平面。

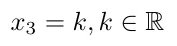
将两个类别分离得最优，如下图所示。

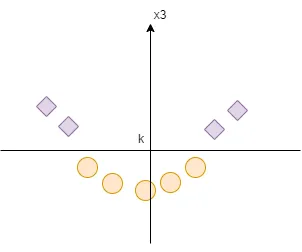
在我们的例子中，函数f是我们所称之为核函数，它将数据投影到一个更高维的空间中，这使得更容易找到一个可以正确识别不同类别数据的超平面。

量子核函数

量子核函数通常通过一个基于量子电路的相似性矩阵来定义，这个矩阵可以是可参数化的，也可以不是。Pennylane和Qiskit都有内建函数，可以创建可以在scikit-learn的SVC中使用的核函数。

量子核函数的项目有几个步骤：

将数据嵌入到量子态中

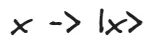
设计出可能是可参数化的或者不可参数化的量子电路。

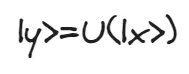
在这个阶段，强烈建议在状态之间以一定的叠加和纠缠程度下工作，以获得量子计算能够提供的最佳结果。

构建相似性矩阵

例子

在这里，我们使用Pennylane设计一个简单的量子核函数，以便与scikit-learn中的SVC一起使用，针对Titanic分类数据集进行预测，即根据年龄、性别和船舱等级等变量来预测一个人是否在Titanic悲剧中幸存下来。

在我们的例子中，我们使用以下变量：

is_child：如果一个人的年龄小于12岁（布尔值）
Pclass_1：如果一个人登上了一等舱（布尔值）
Pclass_2：如果一个人登上了二等舱（布尔值）
Sex_female：如果一个人的性别为女性（布尔值）

如你所见，这是一个非常简单的模型，其中有四个布尔变量。我们使用量子嵌入（基底嵌入）将我们的数据嵌入到量子态中，通过应用Hadamard门将叠加应用于我们的量子比特，并使用CNOT门生成纠缠。

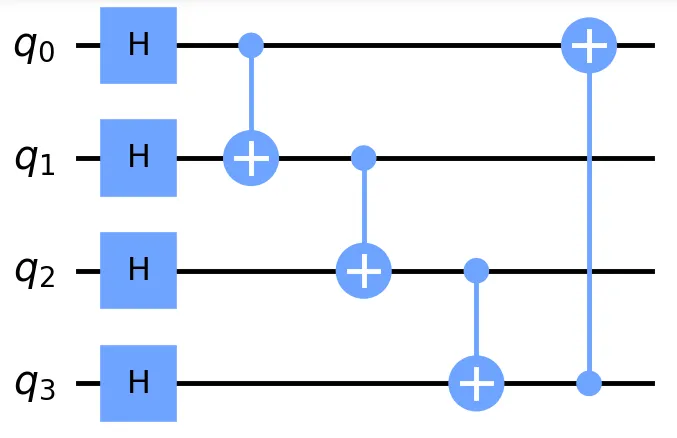
这是一个简单且不可参数化的假设，但它在我们的变量之间生成叠加态和纠缠。

这是创建核函数和支持向量机（SVM）的代码。

import pennylane as qml
from pennylane import numpy as np
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score, precision_score, recall_score
from sklearn.svm import SVC
num_qubits = 4
def layer(x):
    
    qml.BasisEmbedding(x, wires=range(num_qubits))
    
    for j, wire in enumerate(wires):
        qml.Hadamard(wires=[wire])
        if j != num_qubits-1:
            qml.CNOT(wires=[j, j+1])
        else:
            qml.CNOT(wires=[j, 0])
def ansatz(x, wires):
    layer(x)
adjoint_ansatz = qml.adjoint(ansatz)
dev = qml.device("default.qubit", wires=num_qubits, shots=None)
wires = dev.wires.tolist()
@qml.qnode(dev, interface="autograd")
def kernel_circuit(x1, x2):
    ansatz(x1, wires=wires)
    adjoint_ansatz(x2, wires=wires)
    return qml.probs(wires=wires)
def kernel(x1, x2):
    return kernel_circuit(x1, x2)[0]
df_train = pd.read_csv('train.csv')
df_train['Pclass'] = df_train['Pclass'].astype(str)
df_train = pd.concat([df_train, pd.get_dummies(df_train[['Pclass', 'Sex', 'Embarked']])], axis=1)
X_train, X_test, y_train, y_test = train_test_split(df_train.drop(columns=['Survived']), df_train['Survived'], test_size=0.10, random_state=42, stratify=df_train['Survived'])
X_train['Age'] = X_train['Age'].fillna(X_train['Age'].median())
X_test['Age'] = X_test['Age'].fillna(X_test['Age'].median())
X_train['is_child'] = X_train['Age'].map(lambda x: 1 if x < 12 else 0)
X_test['is_child'] = X_test['Age'].map(lambda x: 1 if x < 12 else 0)
cols_model = ['is_child', 'Pclass_1', 'Pclass_2', 'Sex_female']
X_train = X_train[cols_model]
X_test = X_test[cols_model]
X_train = np.array(X_train.values, requires_grad=False)
init_kernel = lambda x1, x2: kernel(x1, x2)
K = qml.kernels.square_kernel_matrix(X_train, init_kernel, assume_normalized_kernel=True)
svm = SVC(kernel=lambda X1, X2: qml.kernels.kernel_matrix(X1, X2, init_kernel)).fit(X_train, y_train)
X_test = np.array(X_test.values, requires_grad=False)
predictions = svm.predict(X_test)
accuracy_score(y_test, predictions)
precision_score(y_test, predictions)
recall_score(y_test, predictions)
f1_score(y_test, predictions, average='macro')
svm1 = SVC(gamma='auto', kernel='rbf')
svm1.fit(X_train, y_train)
y_pred = svm1.predict(X_test)
accuracy_score(y_test, y_pred)
precision_score(y_test, y_pred)
recall_score(y_test, y_pred)
f1_score(y_test, y_pred, average='macro')

结果是：

正如你所看到的，采用RBF核的SVC效果优于我们采用量子核的SVC。我们的量子方法具有良好的精确度，这意味着我们在很大程度上成功避免了误报，但我们的召回率不太好，这意味着我们存在很多错误的否定。

结论

量子核可以成为提高SVM性能的有力工具。然而，正如我们在例子中所看到的，采用简单量子核的SVM无法超越采用RBF核的SVM。量子核需要仔细设计才能与经典技术竞争。