在本文中，我们将看到如何通过使用JAX对环境进行向量化和无缝并行训练几十个智能体来扩展强化学习实验。具体而言，本文涵盖以下内容：

1. JAX基础知识和强化学习的有用功能

2. 向量化环境及其为何如此快速

3. 在JAX中实现环境、策略和Q-learning 

4. 单智能体训练

5. 如何并行训练智能体，以及它有多容易！

JAX基础知识

JAX是由Google开发的又一个Python深度学习框架，被DeepMind等公司广泛使用。

“JAX是自动微分（Autograd）和加速线性代数（XLA，一个TensorFlow编译器）的结合，用于高性能数值计算。”

与大多数Python开发者习惯的不同，JAX不采用面向对象编程（OOP）范 paradigm，而是采用函数式编程（FP）。

简而言之，它依赖于纯函数（确定性且没有副作用）和不可变数据结构（而不是就地修改数据，而是创建具有所需修改的新数据结构）作为主要构建块。结果，FP鼓励更加功能性和数学化的编程方法，非常适合数值计算和机器学习等任务。

让我们通过查看一个Q更新功能的伪代码来说明这两种范式之间的区别：

1. 面向对象的方法依赖于包含各种状态变量（如Q值）的类实例。更新函数被定义为类方法，用于更新实例。

2. 函数式编程方法依赖于纯函数。实际上，这个Q更新是确定性的，因为Q值作为参数传递。因此，对于相同的输入调用该函数将产生相同的输出，而类方法的输出可能取决于实例的内部状态。此外，数组等数据结构在全局范围内定义和修改。

因此，JAX提供了各种函数修饰符在RL环境中特别有用：

vmap（向量化映射）：允许将作用于单个样本的函数应用于批次。例如，如果env.step()是在单个环境中执行一步的函数，那么vmap(env.step)()就是在多个环境中执行一步的函数。换句话说，vmap将函数添加了一个批次维度。

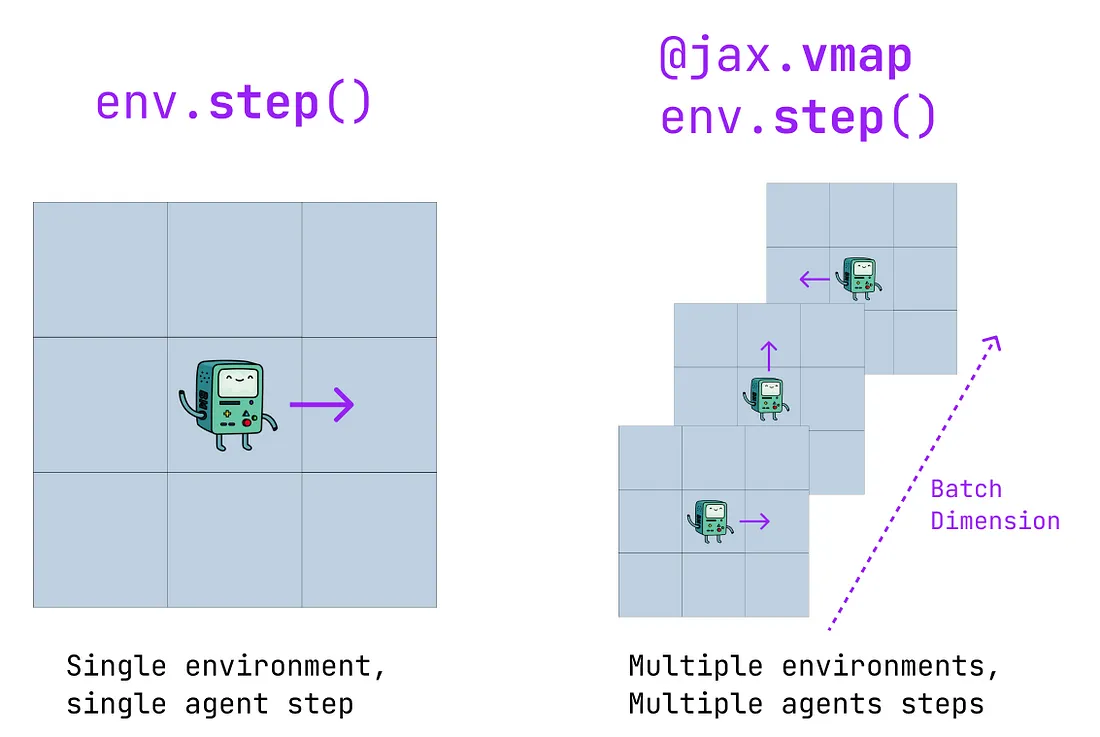
即时编译（jit）：允许JAX对JAX Python函数进行“即时编译”，从而使其与XLA兼容。使用jit编译函数可以显著提高速度（但在首次编译函数时会有一些额外开销）。

并行映射（pmap）：类似于vmap，pmap实现了简单的并行化。然而，它不是在函数上添加批处理维度，而是复制函数并在多个XLA设备上执行。注意：应用pmap时，jit也会自动应用。

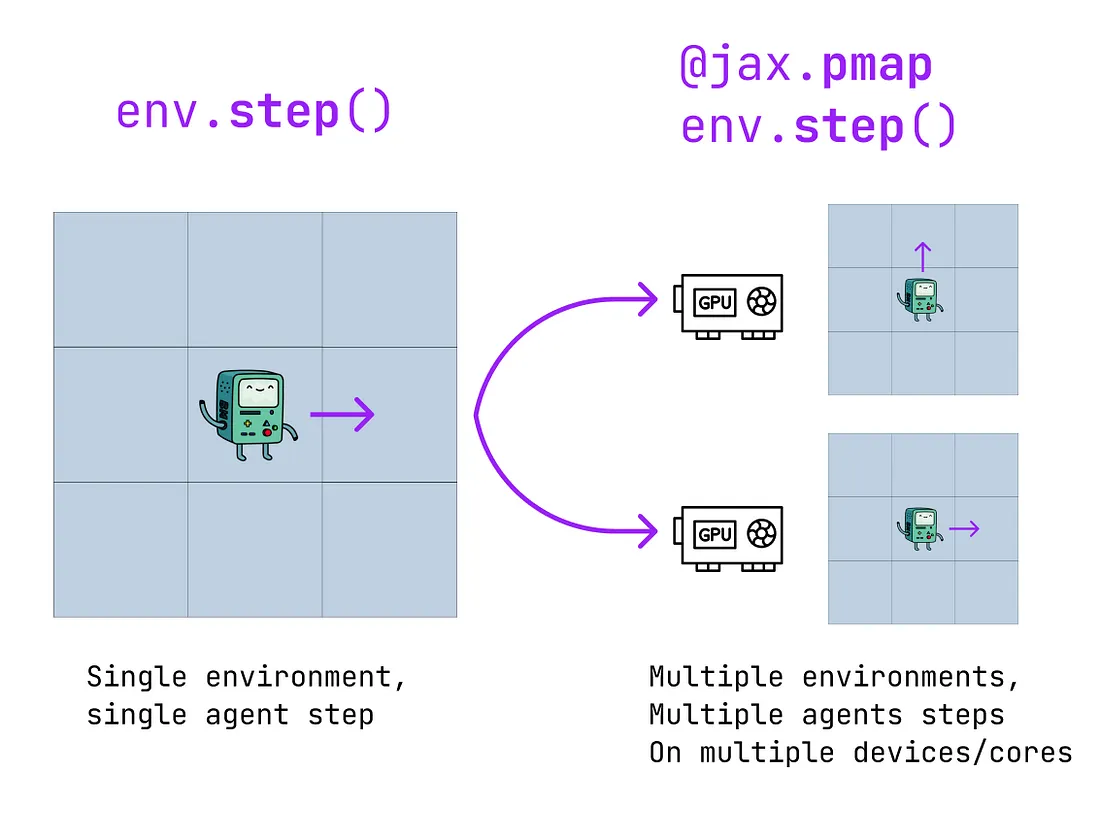
现在我们已经介绍了JAX的基本知识，接下来我们将看到如何通过矢量化环境来获得巨大的加速。

矢量化环境：

首先，什么是矢量化环境，矢量化解决了哪些问题？

在大多数情况下，RL实验被CPU-GPU数据传输放慢。深度学习RL算法（如PPO）使用神经网络来近似策略。

和深度学习中的其他情况一样，神经网络在训练和推理时使用GPU。然而，在大多数情况下，环境在CPU上运行（即使是并行使用多个环境的情况下）。

这意味着选择动作并通过策略（神经网络）从环境中接收观测和奖励的常规RL循环需要在GPU和CPU之间不断交互，这会影响性能。

此外，使用PyTorch等框架而不进行“jitting”可能会导致一些开销，因为GPU可能必须等待Python将观测和奖励从CPU发送回来。

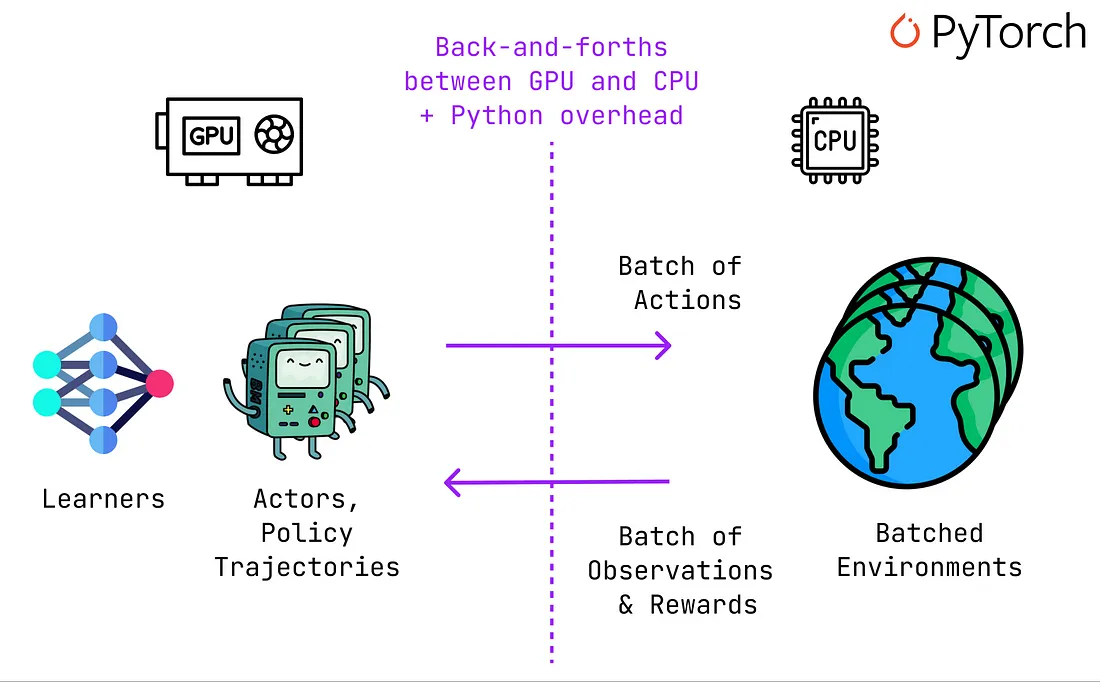
另一方面，JAX使我们能够轻松地在GPU上运行批处理环境，消除了由GPU和CPU之间的数据传输带来的不顺畅。

此外，由于jit将我们的JAX代码编译成XLA，执行过程不再（或至少是较少）受到Python低效率的影响。

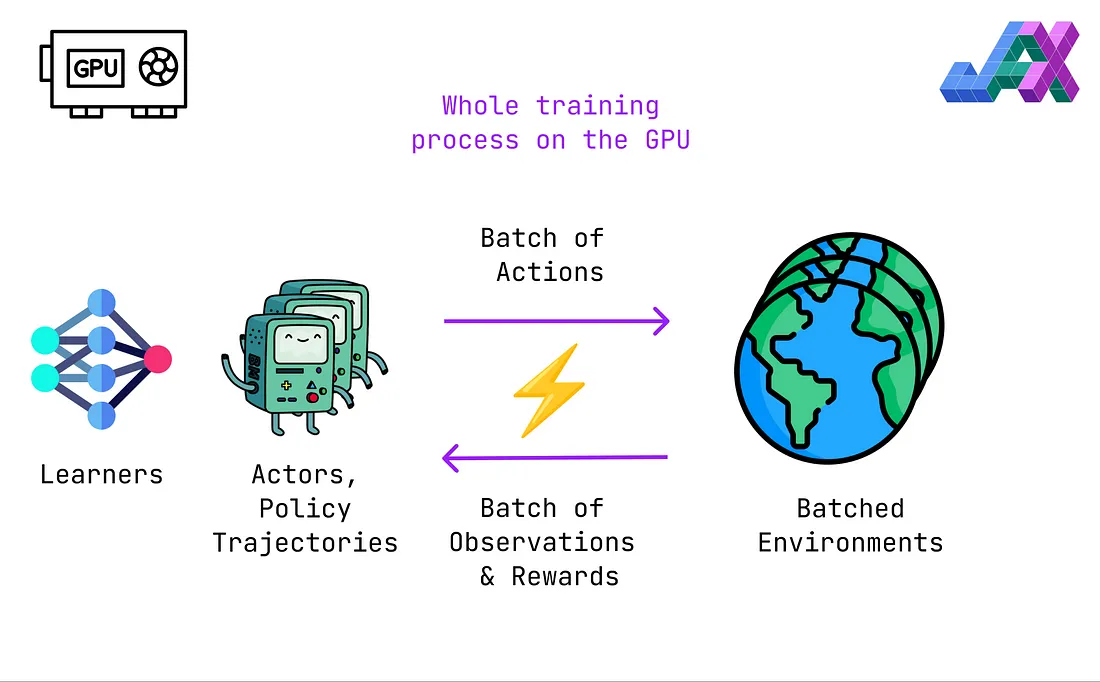
环境、代理和策略的实现：

让我们看一下我们强化学习实验的不同部分的实现。以下是我们需要的基本功能的高级概述：

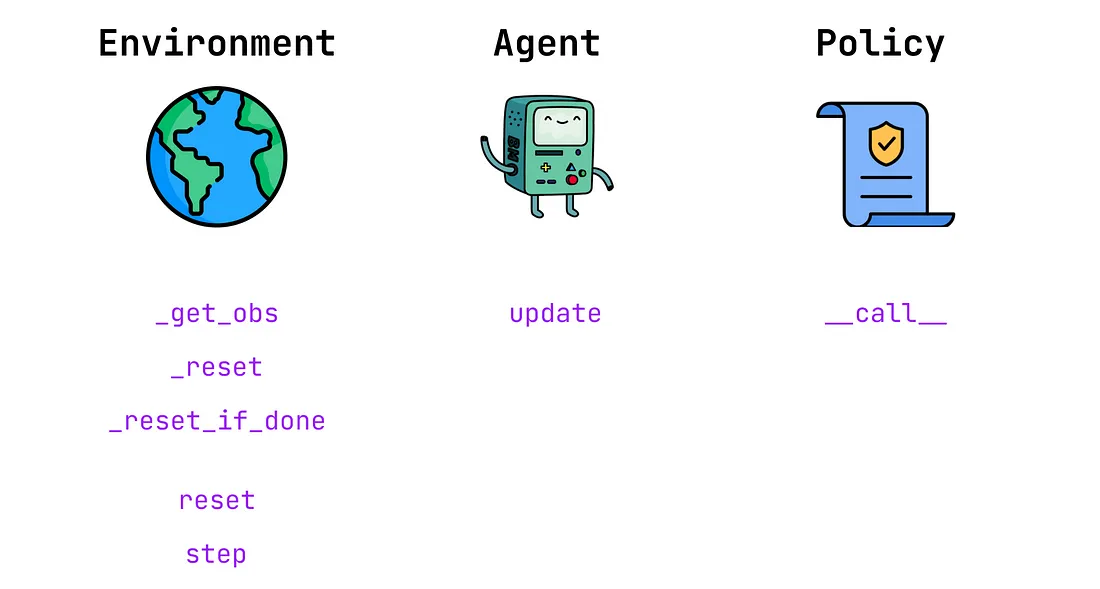
让我们从对环境及其方法的高级概述开始。这是在JAX中实施环境的一般计划。

from abc import ABC, abstractmethod
class BaseEnv(ABC):
    def __init__(self) -> None:
        pass
    # --- Private methods ---
    @abstractmethod
    def _get_obs(self, state):
        pass
    @abstractmethod
    def _reset(self, key):
        pass
    @abstractmethod
    def _reset_if_done(self, env_state, done):
        pass
    # --- Public methods ---
    @abstractmethod
    def reset(self, key):
        pass
    @abstractmethod
    def step(self, env_state, action):
        pass

让我们仔细看一下类方法（作为提醒，以“_”开头的函数是私有的，不能在类的范围之外调用）：

1. _get_obs：该方法将环境状态转换为智能体的观察。在部分可见或随机环境中，应在此处进行应用于状态的处理函数。

2. _reset：由于我们将并行运行多个智能体，所以需要一种方法在一个周期结束后对每个智能体进行个体复位。

3. _reset_if_done：该方法将在每个步骤中调用，并根据“done”标志是否设置为True来触发_reset。

4. reset：该方法在实验开始时被调用，以获得每个智能体的初始状态，以及相关的随机密钥。

5. step：给定一个状态和一个动作，环境返回一个观察（新状态），一个奖励和更新后的“done”标志。

实际上，一个通用的GridWorld环境的实现应该如下：

from functools import partial
import jax.numpy as jnp
from jax import jit, lax
from .base_env import BaseEnv
class GridWorld(BaseEnv):
    def __init__(self, initial_state, goal_state, grid_size) -> None:
        super(GridWorld, self).__init__()
        self.initial_state = initial_state
        self.goal_state = goal_state
        self.grid_size = grid_size
        self.movements = jnp.array([[0, 1], [1, 0], [0, -1], [-1, 0]])
    def _get_obs(self, state):
        return state
    def _reset(self, key):
        return self.initial_state, key
    def _reset_if_done(self, env_state, done):
        key = env_state[1]
        return lax.cond(
            done,
            self._reset,
            lambda key: env_state,
            key,
        )
    def _get_reward_done(self, new_state):
        done = jnp.all(new_state == self.goal_state)
        reward = jnp.int32(done)
        return reward, done
    @partial(jit, static_argnums=(0))
    def step(self, env_state, action):
        state, key = env_state
        action = self.movements[action]
        new_state = jnp.clip(jnp.add(state, action), jnp.array([0, 0]), self.grid_size)
        reward, done = self._get_reward_done(new_state)
        env_state = new_state, key
        env_state = self._reset_if_done(env_state, done)
        new_state = env_state[0]
        return env_state, self._get_obs(new_state), reward, done
    def reset(self, key):
        env_state = self._reset(key)
        new_state = env_state[0]
        return env_state, self._get_obs(new_state)

请注意，如前所述，所有的类方法都遵循函数式编程范式。实际上，在类实例化后，我们从不更新类实例的内部状态。此外，类属性都是常量，在实例化后不会被修改。

让我们仔细看一下：

1. init：在我们的GridWorld环境中，可用的动作是[0, 1, 2, 3]。这些动作使用self.movements转换为一个二维数组，并添加到step函数中的状态中。

2. _get_obs：我们的环境是确定性的和完全可观察的，因此代理直接接收到状态而不是经过处理的观察。

3. _reset_if_done：参数env_state对应于(state, key)元组，其中key是一个jax.random.PRNGKey。如果完成标志设置为True，这个函数简单地返回初始状态，但是在JAX jitted函数中我们无法使用传统的Python控制流。使用jax.lax.cond，我们基本上得到了一个与以下表达式等价的表达式：

def cond(condition, true_fun, false_fun, operand):
  if condition: # if done flag == True
    return true_fun(operand)  # return self._reset(key)
  else:
    return false_fun(operand) # return env_state

4. 步骤：我们将动作转换为移动，并将其添加到当前状态中（jax.numpy.clip 确保智能体保持在网格内）。然后，在检查环境是否需要重置之前，我们更新 env_state 元组。由于在训练过程中频繁使用 step 函数，使用 jitting 可以显著提高性能。@partial(jit, static_argnums=(0, )) 装饰器表示类方法的 “self” 参数应被视为静态的。换句话说，类的属性是常量，在连续调用 step 函数时不会更改。

Q-Learning代理

Q-Learning Agent 的定义由 update 函数、静态学习率和折扣因子组成。

from functools import partial
import jax.numpy as jnp
from jax import jit
from .base_agent import BaseAgent
class Q_learning(BaseAgent):
    def __init__(
        self, key, n_states, n_actions, discount, learning_rate,
    ) -> None:
        super(Q_learning, self).__init__(
            key,
            n_states,
            n_actions,
            discount,
        )
        self.learning_rate = learning_rate
    @partial(jit, static_argnums=(0,))
    def update(self, state, action, reward, done, next_state, q_values):
        update = q_values[state[0], state[1], action]
        update += self.learning_rate * (
            reward + self.discount * jnp.max(q_values[tuple(next_state)]) - update
        )
        return q_values.at[state[0], state[1], action].set(update)

再次变异更新功能时，将“self”参数作为静态参数传递。还要注意，使用set()原地修改了q_values矩阵，并且其值没有作为类属性存储。

Epsilon-贪婪策略

最后，此实验中使用的策略是标准的epsilon-贪婪策略。一个重要的细节是它使用随机的决策，这意味着如果最大的Q值不唯一，动作将从最大的Q值中均匀采样（使用argmax将总是返回第一个具有最大Q值的动作）。这在Q值被初始化为一个零矩阵的情况下尤为重要，因为动作0（向右移动）将总是被选中。

否则，该策略可以通过以下代码片段进行总结：

action = lax.cond(
            explore, # if p < epsilon
            _random_action_fn, # select a random action given the key
            _greedy_action_fn, # select the greedy action w.r.t Q-values
            operand=subkey, # use subkey as an argument for the above funcs
        )
return action, subkey

注意，在JAX中使用一个键时（例如，在这里我们抽取了一个随机浮点数并使用了random.choice），常见的做法是在之后拆分这个键。

from functools import partial
import jax.numpy as jnp
from jax import jit, lax, random
from .base_policy import BasePolicy
class EpsilonGreedy(BasePolicy):
    """
    Epsilon-Greedy policy with random tie-breaks
    """
    def __init__(self, epsilon):
        self.epsilon = epsilon
    @partial(jit, static_argnums=(0, 2))
    def call(self, key, n_actions, state, q_values):
        def _random_action_fn(subkey):
            return random.choice(subkey, jnp.arange(n_actions))
        def _greedy_action_fn(subkey):
            """
            Selects the greedy action with random tie-break
            If multiple Q-values are equal, sample uniformly from their indexes
            """
            q = q_values[state[0], state[1]]
            q_max = jnp.max(q, axis=-1)
            q_max_mask = jnp.equal(q, q_max)
            p = jnp.divide(q_max_mask, q_max_mask.sum())
            choice = random.choice(subkey, jnp.arange(n_actions), p=p)
            return jnp.int32(choice)
        explore = random.uniform(key) < self.epsilon
        key, subkey = random.split(key)
        action = lax.cond(
            explore,
            _random_action_fn,
            _greedy_action_fn,
            operand=subkey,
        )
        return action, subkey

单代理训练循环：

现在我们拥有了所有所需的组件，让我们训练一个单个的代理。

这里是一个Python训练循环，正如你所看到的，我们基本上是使用策略选择一个动作，执行环境中的一步，并更新Q值，直到一个回合结束。然后我们重复这个过程进行N个回合。正如我们一会儿会看到的，这种训练代理的方法相当低效，然而，它以一种可读的方式总结了算法的关键步骤。

def train_single_agent_n_episodes(n_episodes=10_000):    
    key = random.PRNGKey(0)
    q_values = jnp.zeros([GRID_SIZE[0], GRID_SIZE[1], N_ACTIONS], dtype=jnp.float32)
    env_state, obs = env.reset(key) 
    done = False
    for _ in tqdm(range(n_episodes)):
        done = False
        while not done:
            state, _ = env_state
            action, key = policy(key, N_ACTIONS, state, q_values)
            env_state, obs, reward, done = env.step(env_state, action)
            q_values = agent.update(state, action, reward, done, obs, q_values)

在一台单个 CPU 上，我们以每秒 881 个 episodes 和 21,680 步的速度，在 11 秒内完成了 10,000 个 episodes。

100%|██████████| 10000/10000 [00:11<00:00, 881.86it/s]
Total Number of steps: 238 488
Number of steps per second: 21 680

现在，让我们使用JAX语法复制相同的训练循环。以下是对rollout函数的高级描述。

总结一下，这个滚动函数：

1. 使用jax.numpy.zeros将观测、奖励和完成标志初始化为空数组，维度与时间步数相等。将Q-值初始化为空矩阵，形状为[timesteps+1, grid_dimension_x, grid_dimension_y, n_actions]。

2. 调用env.reset()函数获取初始状态。

3. 使用jax.lax.fori_loop()函数调用fori_body()函数N次，其中N是时间步数参数。

4. fori_body()函数的行为类似于之前的Python循环。在选择动作、执行步骤和计算Q更新之后，我们在原地更新obs、rewards、done和q_values数组（Q更新针对时间步t+1）。

@loop_tqdm(TIME_STEPS)
@jit
def fori_body(i:int, val:tuple):
    env_states, action_key, all_obs, all_rewards, all_done, all_q_values = val
    states, _ = env_states
    q_values = all_q_values[i, :, :, :]
    
    # action selection, step and q-update
    actions, action_key = policy(action_key, N_ACTIONS, states, q_values)
    env_states, obs, rewards, done = env.step(env_states, actions)
    q_values = agent.update(states, actions, rewards, done, obs, q_values)
    
    # update observations, rewards, done flag and q_values
    all_obs = all_obs.at[i].set(obs)
    all_rewards = all_rewards.at[i].set(rewards)
    all_done = all_done.at[i].set(done)
    all_q_values = all_q_values.at[i+1, :, :, :].set(q_values)
    val = (env_states, action_key, all_obs, all_rewards, all_done, all_q_values)
    return val
def rollout(key: random.PRNGKey, timesteps:int):
    # initialize obs, rewards, done and q_values with an added time index
    all_obs = jnp.zeros([timesteps, 2])
    all_rewards = jnp.zeros([timesteps], dtype=jnp.int32)
    all_done = jnp.zeros([timesteps], dtype=jnp.bool_)
    # q_values has first dimension = timesteps +1, as the update targets time step t+1
    all_q_values = jnp.zeros([timesteps+1, GRID_SIZE[0], GRID_SIZE[1], N_ACTIONS], dtype=jnp.float32)
    # random keys used for policy / action selection
    action_key = random.PRNGKey(0)
    env_states, _ = env.reset(key)
    
    val_init = (env_states, action_key, all_obs, all_rewards, all_done, all_q_values)
    val = lax.fori_loop(0, timesteps, fori_body, val_init)
    
    return val

这种额外的复杂性导致了85倍的加速，我们现在以大约每秒1.83百万步的速度训练我们的代理。请注意，这里的训练是在单个CPU上进行的，因为环境是简单的。

然而，当应用于复杂环境和从多个GPU中受益的算法时，端到端向量化效果更好（Chris Lu的文章报告了一个令人震惊的4000倍加速，用CleanRL PyTorch实现的PPO与JAX重现对比）。

100%|██████████| 1000000/1000000 [00:00<00:00, 1837563.94it/s]
Total Number of steps: 1 000 000
Number of steps per second: 1 837 563

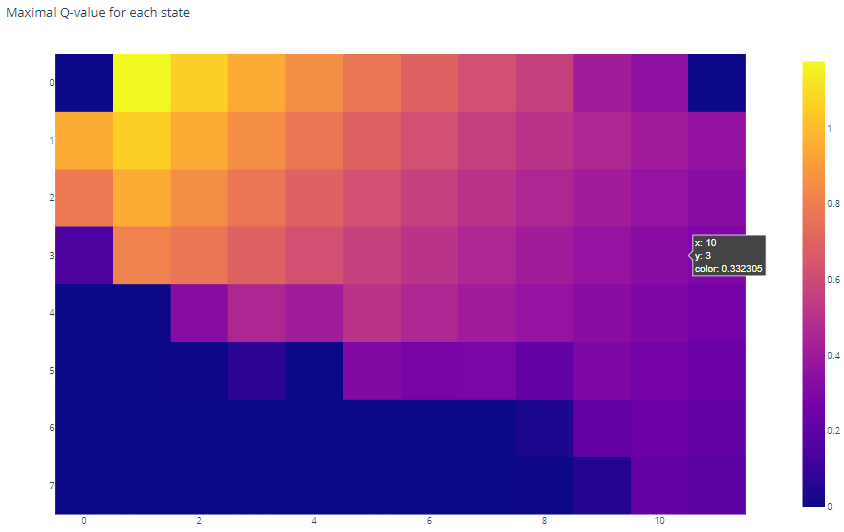
训练完我们的智能体后，我们绘制了GridWorld中每个单元格（即状态）的最大Q值，并观察到它已经有效地学会了从初始状态（右下角）到目标状态（左上角）的移动。

并行代理训练循环：

正如承诺的那样，现在我们已经编写了训练单个代理所需的函数，我们几乎没有什么工作剩下来，就可以在批处理环境中并行训练多个代理！

多亏了vmap，我们可以快速地将我们之前的函数转换为批处理数据上的工作方式。我们只需要指定预期的输入和输出形状，例如对于env.step：

1. in_axes = ((0, 0), 0)表示输入形状，由env_state元组（维度（0, 0））和观察值（维度0）组成。

2. out_axes = ((0, 0), 0, 0, 0)表示输出形状，其中输出为((env_state)，obs, reward, done)。

3. 现在，我们可以在一系列的env_states和actions上调用v_step，并接收一系列处理过的env_states、observations、rewards和done标志。

4. 请注意，我们还为了性能将所有的批处理函数进行了jit编译（可以说，对env.reset()进行jit编译是不必要的，因为它在我们的训练函数中只调用一次）。

v_reset = jit(vmap(
                env.reset,
                out_axes=((0, 0), 0),  # ((env_state), obs)
            ))
v_step = jit(vmap(
                env.step,
                in_axes=((0, 0), 0),  # ((env_state), action)
                out_axes=((0, 0), 0, 0, 0),  # ((env_state), obs, reward, done)
            ))
v_update = jit(vmap(
                agent.update,
                in_axes=(0, 0, 0, 0, 0, -1),
                # iterate through the last dimension of 
                # agent.update's output (i.e. batch dim)
                out_axes=-1,
                ))
v_policy = jit(vmap(
                policy.call,
                in_axes=(0, None, 0, -1),  # (keys, n_actions, state, q_values)
                ),
                static_argnums=(1,),
            )

我们需要进行的最后一次调整是为我们的数组添加一个批量维度，以考虑每个代理的数据。

通过这样做，我们可以得到一个允许我们并行训练多个代理的函数，与单个代理函数相比，只需要做出最小的调整。

N_ENV = 30
TIME_STEPS = 100_000
key = random.PRNGKey(SEED)
keys = random.split(key, N_ENV)
@jit
def fori_body(i:int, val:tuple):
    env_states, action_keys, all_obs, all_rewards, all_done, all_q_values = val
    states, _ = env_states
    q_values = all_q_values[i, :, :, :, :]
    actions, action_keys = v_policy(action_keys, N_ACTIONS, states, q_values)
    env_states, obs, rewards, done = v_step(env_states, actions)
    q_values = v_update(states, actions, rewards, done, obs, q_values)
    
    all_obs = all_obs.at[i].set(obs)
    all_rewards = all_rewards.at[i].set(rewards)
    all_done = all_done.at[i].set(done)
    all_q_values = all_q_values.at[i+1, :, :, :, :].set(q_values)
    val = (env_states, action_keys, all_obs, all_rewards, all_done, all_q_values)
    return val
def single_agent_rollout(keys: random.PRNGKey, timesteps: int, n_env: int):
    all_obs = jnp.zeros([timesteps, n_env, 2])
    all_rewards = jnp.zeros([timesteps, n_env], dtype=jnp.int32)
    all_done = jnp.zeros([timesteps, n_env], dtype=jnp.bool_)
    # q_values has first dimension = timesteps +1, as the update targets time step t+1
    all_q_values = jnp.zeros([timesteps+1, GRID_SIZE[0], GRID_SIZE[1], N_ACTIONS, n_env], dtype=jnp.float32)
    action_keys = random.split(random.PRNGKey(0), n_env)
    env_states, _ = v_reset(keys)
    
    val_init = (env_states, action_keys, all_obs, all_rewards, all_done, all_q_values)
    val = lax.fori_loop(0, timesteps, fori_body, val_init)
    env_states, action_keys, all_obs, all_reward, all_done, all_q_values = val
    
    return all_obs, all_reward, all_done, all_q_values
all_obs, all_reward, all_done, all_q_values = single_agent_rollout(keys, TIME_STEPS, N_ENV)

我们使用这个版本的训练函数得到了类似的表现。

100%|██████████| 100000/100000 [00:02<00:00, 49036.11it/s]
Total Number of steps: 100 000 * 30 = 3 000 000
Number of steps per second: 49 036 * 30 = 1 471 080