介绍

时间序列数据记录了随时间变化的观测结果，它是经济学、金融学、气象学等多个领域的重要组成部分。准确预测时间序列数据对决策和计划至关重要。然而，并非所有时间序列数据都是平稳的，即其统计特性会随时间变化。预测非平稳时间序列是一项具有挑战性的任务，需要特殊的技术和模型来处理数据的动态性。本文将探讨非平稳时间序列的概念，以及它所带来的挑战和用于在这种情况下进行预测的方法。

在数据的领域中，对非平稳时间序列进行预测就像是航行在一条不断变化的河流中，而适应性和精确性则是指南针和地图。

了解平稳性

在深入研究非平稳时间序列之前，理解平稳性的概念至关重要。平稳时间序列是指其统计特性随时间不变的序列。这些特性包括均值、方差和自相关性。实质上，平稳时间序列具有恒定的均值和方差，并在其观测中展示一致的模式和趋势。由于遵循稳定的统计特性，平稳数据更容易建模和预测。

非平稳时间序列的挑战

另一方面，非平稳时间序列的统计特性随时间变化。这使得与非平稳时间序列的工作和预测更具挑战性。非平稳时间序列所面临的主要挑战包括：

趋势：非平稳数据通常显示出趋势，即在一个方向上的长期系统性移动，可能是上升趋势或下降趋势。识别和消除趋势对于进行预测至关重要。

季节性：季节性是非平稳数据的另一个常见特征。它代表在固定间隔内发生的周期性波动，例如每天、每月或每年的模式。考虑到季节性对于进行准确预测至关重要。

异方差性：非平稳时间序列经常显示出随时间变化的波动级别或方差。这种异方差性可能使得难以建立假设具有恒定方差的预测模型。

非平稳时间序列的预测技术

为了应对非平稳时间序列数据带来的挑战，已经发展了各种预测技术和模型。其中一些常用的方法包括：

差分法：处理非平稳性的主要方法之一是进行差分。这涉及计算相邻观测值之间的差异，有助于稳定均值，并消除趋势和季节性。

季节分解法：时间序列的季节分解（STL）方法将时间序列分解为趋势、季节和残差组成部分。这种分解允许对每个组成部分进行建模和预测，从而更容易处理非平稳性。

指数平滑法：指数平滑方法（如Holt-Winters）对具有趋势和季节性的时间序列具有良好的预测效果。这些方法为过去的观测值分配不同的权重，给予近期数据点更大的重要性。

ARIMA模型：自回归积分滑动平均（ARIMA）模型广泛用于非平稳时间序列。ARIMA模型涉及对数据进行差分，使其变为平稳，然后使用自回归和移动平均的组件进行建模。

季节性ARIMA：对于同时具有趋势和季节性的时间序列，季节性ARIMA模型（SARIMA）通过结合季节性差分和季节性自回归与移动平均的组件来扩展ARIMA框架。

状态空间模型：状态空间模型（如卡尔曼滤波器）为建模和预测非平稳时间序列提供了灵活的框架。这些模型可以捕捉数据中的复杂动态和结构变化。

代码

预测非平稳时间序列通常涉及一系列步骤，包括数据预处理、模型选择、训练和绘制结果。以下是使用ARIMA模型对非平稳时间序列进行预测的Python代码示例，使用了一个数据集和绘图：

# Import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller
# Generate or load a non-stationary time series dataset
# For demonstration, we'll generate a simple non-stationary dataset
np.random.seed(42)
# Generate a non-stationary time series with a trend and seasonality
t = np.arange(1, 101)
seasonal_component = 10 * np.sin(0.2 * t)
trend_component = 0.5 * t
noise = np.random.normal(0, 2, 100)
data = seasonal_component + trend_component + noise
# Create a pandas DataFrame from the dataset
df = pd.DataFrame({'Data': data})
# Plot the original time series data
plt.figure(figsize=(12, 6))
plt.plot(df.index, df['Data'], label='Original Data')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Non-Stationary Time Series Data')
plt.legend()
plt.show()
# Check for stationarity using Augmented Dickey-Fuller test
def adf_test(series):
    result = adfuller(series)
    print('ADF Statistic:', result[0])
    print('p-value:', result[1])
    print('Critical Values:', result[4])
adf_test(df['Data'])
# Differencing to make the time series stationary
df['Differenced_Data'] = df['Data'] - df['Data'].shift(1)
df = df.dropna()
# Plot the differenced time series data
plt.figure(figsize=(12, 6))
plt.plot(df.index, df['Differenced_Data'], label='Differenced Data')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Stationary Time Series Data')
plt.legend()
plt.show()
# ACF and PACF plots for determining ARIMA orders
plt.figure(figsize=(12, 6))
plot_acf(df['Differenced_Data'], lags=20, ax=plt.gca())
plt.title('ACF Plot')
plt.show()
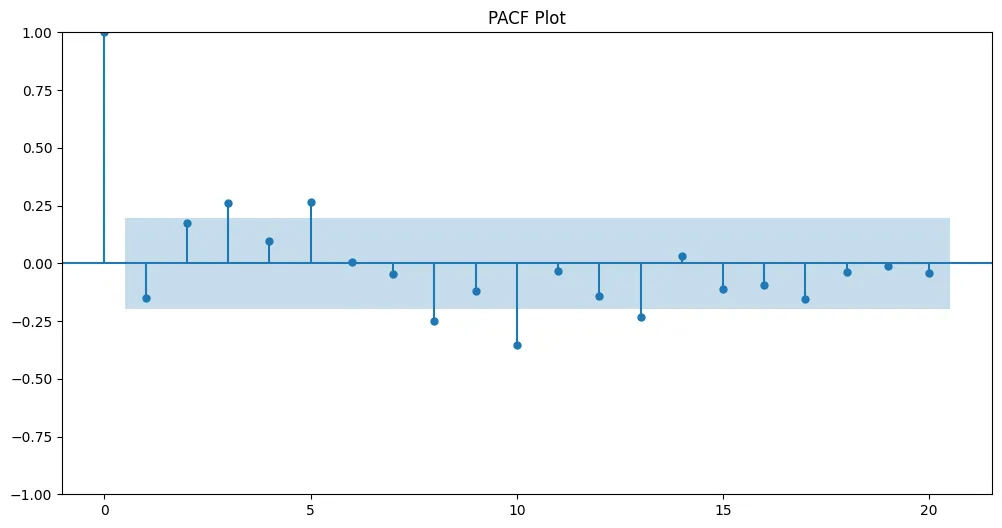
plt.figure(figsize=(12, 6))
plot_pacf(df['Differenced_Data'], lags=20, ax=plt.gca())
plt.title('PACF Plot')
plt.show()
# Split the data into training and testing sets
train_size = int(0.8 * len(df))
train, test = df['Differenced_Data'][:train_size], df['Differenced_Data'][train_size:]
# Fit an ARIMA model to the training data
model = ARIMA(train, order=(1, 1, 1))
model_fit = model.fit()
# Forecast the test data
forecast = model_fit.forecast(steps=len(test))
# Calculate prediction intervals
residuals = test - forecast
prediction_interval = 1.96 * np.std(residuals)  # 1.96 for a 95% prediction interval
# Plot the forecasts and the actual values with prediction intervals
plt.figure(figsize=(12, 6))
plt.plot(df.index[train_size:], test, label='Actual')
plt.plot(df.index[train_size:], forecast, label='Forecast', color='red')
plt.fill_between(df.index[train_size:], forecast - prediction_interval, forecast + prediction_interval, color='pink', alpha=0.3)
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('ARIMA Forecasting with Prediction Intervals')
plt.legend()
plt.show()

该代码生成了一个非平稳的时间序列，通过差分将其转化为平稳序列，使用自相关函数图和偏自相关函数图确定ARIMA模型的阶数，然后预测测试数据。结果被绘制出来以可视化预测值与实际数据之间的关系。

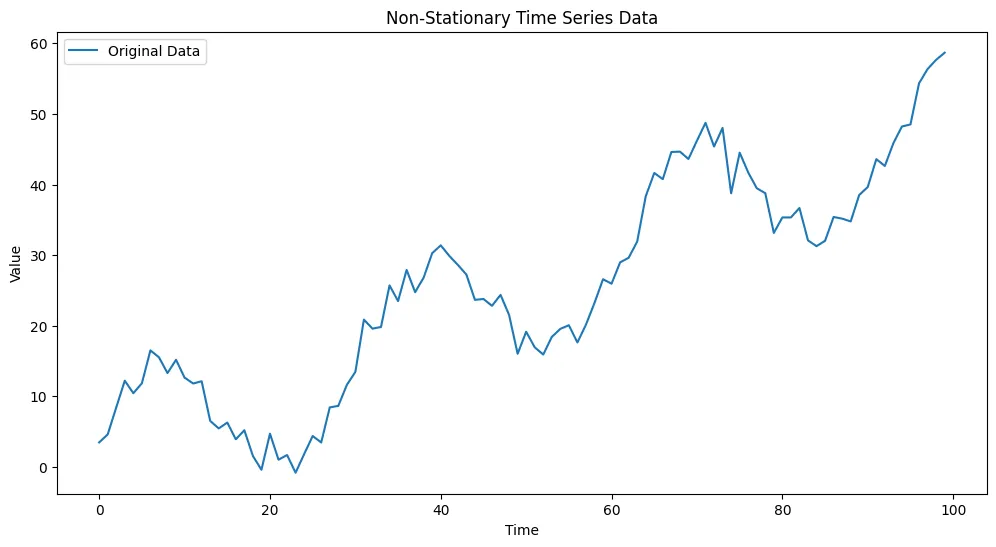
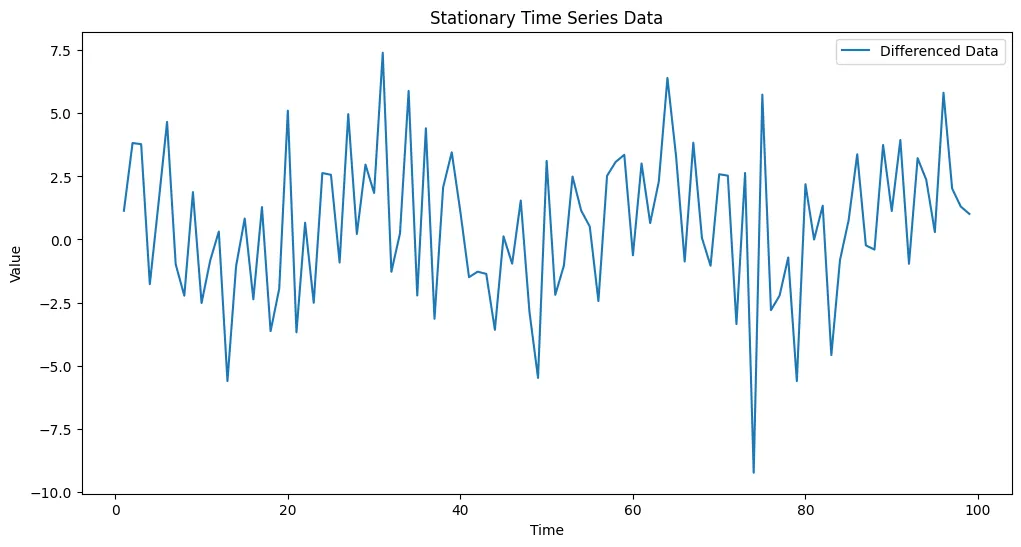
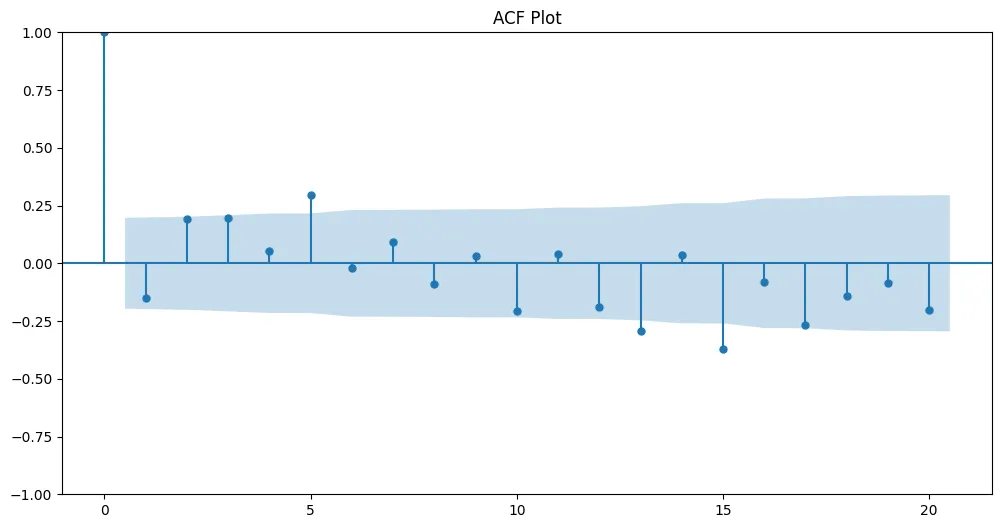
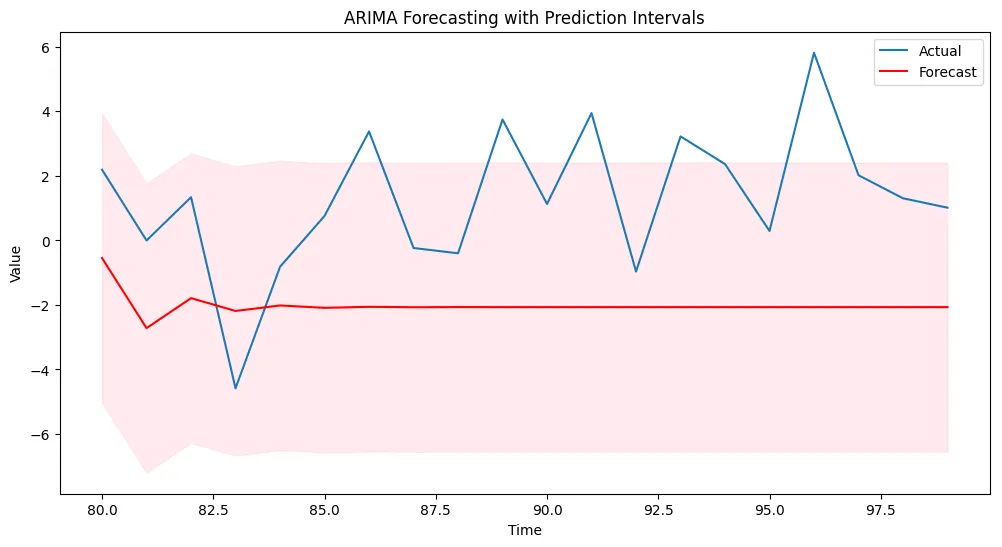
请注意，在现实世界的情境中，通常会从文件或数据库中加载时间序列数据。此外，根据你特定的数据集特征，你可能需要对ARIMA模型参数进行微调。

结论

预测非平稳时间序列是各个领域中一项复杂且重要的任务。认识到非平稳性带来的挑战，如趋势、季节性和异方差性，是开发准确预测的第一步。为了应对这些挑战，已经开发出各种技术和模型，包括差分、季节性分解、指数平滑、ARIMA模型和状态空间模型。这些方法使分析人员能够在面对非平稳时间序列数据时作出更加明智的决策和预测，最终提高他们规划、分配资源和应对变化情况的能力。