介绍

在优化领域，无处不在的复杂性问题中，和谐搜索算法（HSA）以和谐和悦的方式解决复杂问题而崭露头角。从音乐的和谐创作中汲取灵感，HSA在广阔的搜索空间中协调解的收敛。本文将探索和谐搜索算法的原理、机制、应用和优势，为我们揭示它是如何将各种元素融合成最优解的解决方案。

在优化领域中，复杂性可能令人迷惑，“和谐追求优化：和谐搜索算法”提醒我们，即使在最复杂的问题交织中，通过数学精确和探索的和谐旋律也可以找到最甜美的解决方案。

从音乐到优化的和谐

HSA的起源可以追溯到音乐创作艺术。创作和谐旋律的过程涉及将个别音符组合成具有美丽和秩序共鸣的音乐作品。同样，HSA通过优化的方式将个别解决方案结合在一起，创造出和谐。该算法于21世纪初问世，从音符和和弦的韵律平衡中汲取灵感，以编排复杂问题的最优解。

原则和机制

HSA通过音乐的观点进行优化，体现了几个关键原则：

1. 和谐记忆的初始化：HSA通过随机解决方案初始化记忆矩阵，象征着个别音符。
2. 和谐的生成：通过考虑现有记忆矩阵的值来创建新的和谐（解决方案）。和谐的生成是由音高调整和即兴创作引导的，让人想起音乐创作。
3. 目标函数评估：根据问题的目标函数评估每个和谐的适应性。在追求最佳和谐的过程中，HSA努力找到最好的“旋律”。
4. 记忆矩阵的更新：基于新的和谐评估，更新记忆矩阵。最好的和谐被保留在记忆中，以确保保留了最优旋律的“音符”。
5. 收敛和停止准则：HSA继续和谐解决方案和更新记忆矩阵，直到满足收敛准则或达到指定的迭代次数。

应用领域

和谐搜索算法在各个领域中都有应用：

1. 工程设计：应用于优化复杂工程设计，包括结构、机械和系统设计。
2. 数据挖掘和机器学习：在机器学习中，用于超参数调优、特征选择和神经网络架构优化。
3. 运筹学：HSA组合优化问题，如旅行推销员问题、作业调度和资源分配。
4. 环境建模：在环境科学中，辅助生态建模、栖息地保护和土地利用规划。
5. 能源系统：优化能源资源分配、需求侧管理和可再生能源在电力系统中的整合。
6. 金融模型：用于投资组合优化、风险评估和金融行业交易策略的开发。

优势和挑战

和谐搜索算法具有以下优势：

全局探索：HSA的即兴性使其能够广泛探索解空间，寻求全局优解。
适应性：它适应问题景观的变化，确保找到的和谐保持最优。
简单性：该算法的简单性和直观性使其适用于各种优化问题。

同时也存在一些挑战：

参数调整：像许多优化算法一样，HSA可能需要参数调整才能达到特定问题的最佳性能。
计算时间：复杂问题可能需要大量的计算资源和时间才能达到收敛。

代码

在Python中实现和谐搜索算法（HSA），并包含绘图，需要将算法适应特定的优化问题。在下面的示例中，我将为您提供一个使用基本二次函数的简化的HSA示例，并包含一个收敛图。您可以根据自己的问题调整此代码。

在此示例中，我们将使一个简单的二次函数最小化。

import numpy as np
import matplotlib.pyplot as plt
# Define the objective function (replace with your specific problem)
def objective_function(x):
    return x[0]**2 + x[1]**2  # Example: Minimizing a simple quadratic function
# HSA Parameters
harmony_memory_size = 10
max_iterations = 50
pitch_adjustment_rate = 0.7
bandwidth = 0.1
# Define the search space bounds (replace with your specific problem's bounds)
lower_bound = -10
upper_bound = 10
# Initialize harmony memory with random solutions
harmony_memory = np.random.uniform(lower_bound, upper_bound, (harmony_memory_size, 2))
# List to store the best fitness values over iterations
best_fitness_history = []
# Main optimization loop
for iteration in range(max_iterations):
    # Generate a new harmony (solution) through pitch adjustment and improvisation
    new_harmony = np.zeros(2)
    for i in range(2):
        if np.random.rand() < pitch_adjustment_rate:
            # Pitch adjustment
            random_index = np.random.randint(harmony_memory_size)
            new_harmony[i] = harmony_memory[random_index, i]
        else:
            # Improvisation
            new_harmony[i] = np.random.uniform(lower_bound, upper_bound)
    # Evaluate the fitness of the new harmony
    new_fitness = objective_function(new_harmony)
    # Update the harmony memory if the new harmony is better
    if not best_fitness_history or new_fitness < min(best_fitness_history):
        best_fitness_history.append(new_fitness)
        if len(best_fitness_history) > harmony_memory_size:
            worst_index = best_fitness_history.index(max(best_fitness_history))
            harmony_memory[worst_index] = new_harmony


# Plot the convergence curve
plt.figure()
plt.plot(range(len(best_fitness_history)), best_fitness_history, 'b-')
plt.xlabel("Iterations")
plt.ylabel("Best Fitness")
plt.title("HSA Convergence")
plt.grid(True)
plt.show()
print("Best solution found: ", harmony_memory[np.argmin(best_fitness_history)])
print("Best fitness: ", min(best_fitness_history))

在此代码中，我们使用一个基本的二次函数作为目标函数进行最小化。将objective_function替换为您问题的具体适应度函数。该代码模拟了HSA的搜索过程，并可视化迭代的收敛过程。

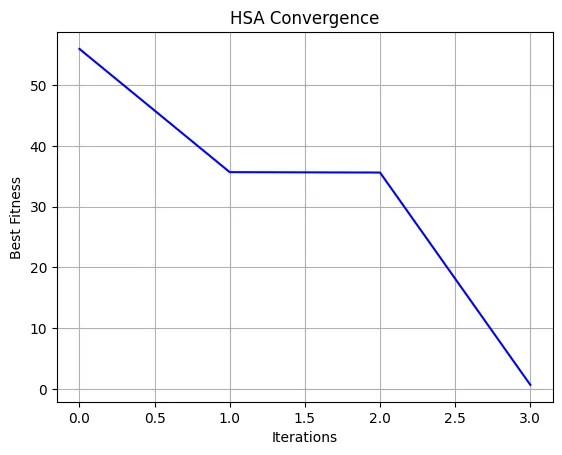
Best solution found:  [-5.19947621  0.58259612]
Best fitness:  0.6481078675672075

通过调整参数、搜索空间边界和目标函数来定制代码。

结论

和谐搜索算法在优化领域中形成了一种和谐的交响乐。从音乐的艺术创作中汲取灵感，HSA在复杂而动态的景观中编排出一场和谐的解决方案之舞。它探索、适应和创造最佳解决方案的能力使其成为优化算法乐团中值得关注的一员。当我们航行于问题解决的错综复杂的作曲中时，和谐搜索算法提醒我们，即使在最复杂的旋律中，只要采取正确的方法，和谐与优化也能被找到。