介绍

最小绝对收缩和选择算子（LASSO）是一种回归分析方法，它同时执行变量选择和正则化，以提高其生成的统计模型的预测精度和可解释性。它最初由Robert Tibshirani于1996年引入，此后已成为数据科学的基本工具，尤其是在预测因子数量超过观测数量的情况下。

基本概念与数学公式

LASSO的关键思想是对模型参数的绝对值之和施加约束。这种约束的效果是将最不重要的变量的系数缩小到零，从而有效地将它们从模型中排除。在数学上，LASSO解决方案是通过最小化误差平方和（就像普通的最小二乘回归一样）来找到的，并添加与系数绝对值之和成比例的惩罚。这可以表示为：

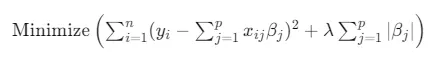
响应变量为yi，预测因子为xij，待估计的系数为βj，观测值的数量为n，预测因子的数量为p，λ是一个调整参数，用于控制惩罚的强度。

变量选择和正则化

LASSO最吸引人的方面之一就是其进行变量选择的能力。这在处理高维数据的上下文中特别有用，因为许多变量可能是相关的或不相关的。通过将一些系数缩减到零，LASSO有效地将这些变量从模型中移除，从而自动进行特征选择。

另一方面，正则化是指为了防止过拟合而向模型中添加信息的过程，通常是通过对模型的复杂度施加惩罚来实现的。在LASSO中，系数的绝对和作为一个正则化项。这不仅有助于特征选择，还通过防止模型变得过于复杂，改善了模型的泛化能力。

调整参数的选择

在LASSO中，调整参数λ的选择至关重要。它控制了模型的拟合优度与系数幅度之间的平衡。λ的值非常高会导致过小的惩罚从而产生欠拟合，而λ的值非常低可能不会足够地惩罚它们，导致过拟合。λ的最优值通常通过交叉验证来选择。

应用和局限性

LASSO因其在处理高维数据时的简单性和效率，在金融、基因组学和市场营销等多个领域得到了广泛应用。在可解释性重要的预测建模中特别有用。

然而，LASSO也有局限性。它倾向于仅从一组高度相关的变量中选择一个变量，这在某些情况下可能是一个缺点。此外，当预测因子的数量大于观测值的数量时，LASSO在饱和之前最多只能选择n个变量。

代码

要在Python中实现最小绝对收缩和选择算子（LASSO），我们可以使用scikit-learn库，该库为LASSO回归提供了一个易于使用的界面。让我们进行一个完整的示例，我们将加载一个数据集，应用LASSO回归，并绘制结果。

逐步实现

1. 导入必要的库

• numpy用于数值运算。
• matplotlib用于绘图。
• sklearn用于机器学习工具。

2. 加载数据集

• 我们可以使用sklearn中的内置数据集进行演示。

3. 将数据集拆分为训练集和测试集

• 这有助于评估我们模型的性能。

4. 应用LASSO回归

• 我们将使用sklearn.linear_model中的Lasso。
• 我们还需要为正则化参数alpha（等同于LASSO公式中的λ）选择一个值。

5. 评估模型

• 我们将检查模型在测试集上的性能。

6. 绘制结果

• 我们可以绘制模型的系数来查看哪些特征已被选择。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
# Load a dataset
X, y = datasets.load_diabetes(return_X_y=True)
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Apply LASSO Regression
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
# Predict and evaluate the model
y_pred = lasso.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
# Plot the coefficients
plt.figure(figsize=(10, 6))
plt.plot(lasso.coef_, marker='o')
plt.title("LASSO Coefficients")
plt.xlabel("Coefficient Index")
plt.ylabel("Coefficient Magnitude")
plt.show()

在这段代码中：

• 我们使用了 sklearn.datasets 中的糖尿病数据集。
• alpha 设置为 0.1，但你可能需要根据交叉验证来调整这个值。
• 该图将显示哪些系数已经被降至零，指示了 LASSO 认为不太重要的特征。

Mean Squared Error: 2798.193485169719

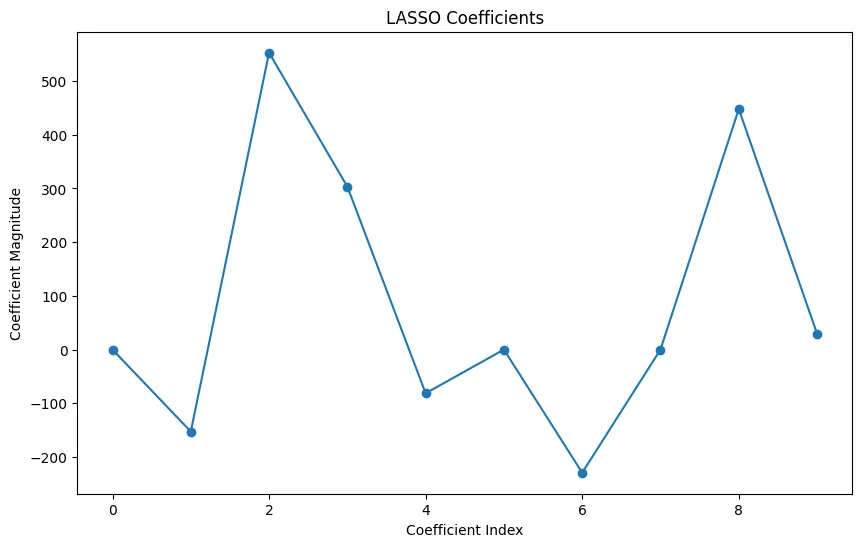
请记住，对于真实世界的应用程序，你会在特征选择、预处理以及使用交叉验证等技术调整正则化参数上花费更多时间。

结论

总之，LASSO是一种强大的方法，它将变量选择与正则化相结合，产生的模型不但精确，也易于理解。它轻松处理高维数据的能力，使其成为数据科学领域的首选方法。然而，它的局限性需要谨慎应用，并理解它可能不适用于每个数据集或问题。