介绍

偏差-方差权衡是机器学习中的一个关键概念，它是模型构建和预测中挑战与策略的基础。它抓住了预测模型中可能出现的两种基本误差来源之间权衡的本质：一是由学习算法中错误假设引起的偏差，二是由于对训练数据变化过于敏感而产生的方差。理解这种权衡对于机器学习领域的新手和资深从业者都至关重要，因为它指导他们选择正确的算法，调整模型参数，并最终实现能够很好地泛化到新的、未见过的数据的模型。本文深入探讨了偏差-方差权衡的复杂性，通过理论解释和实际的Python代码示例阐述了其重要性，因此提供了这一重要机器学习概念的全面概览。

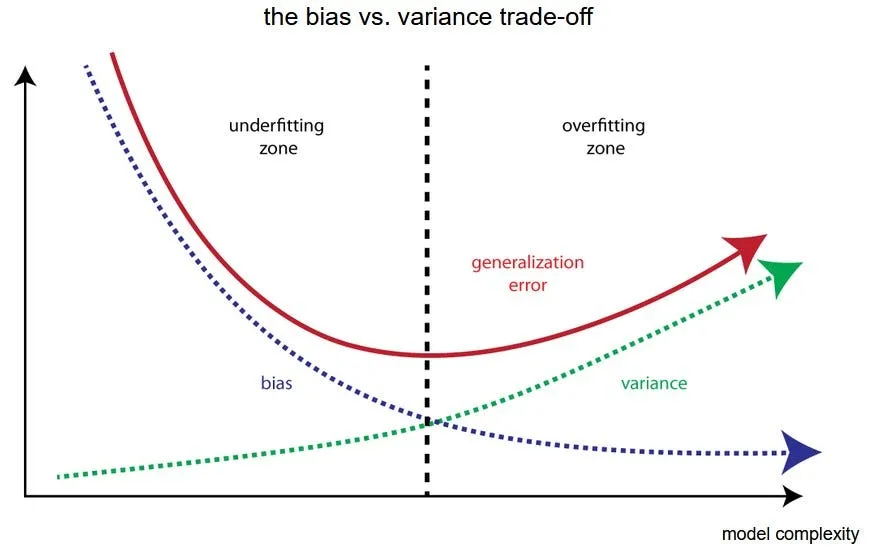
了解偏差和方差

1. 偏差：偏差指的是通过简化模型来近似一个可能很复杂的现实世界问题所引入的错误。高偏差可能导致算法错过特征与目标输出之间的相关关系（欠拟合）。这通常发生在过于简单的模型中。
2. 方差：方差指的是模型对训练数据集中小的波动的敏感性导致的错误。高方差可能导致算法拟合训练数据中的随机噪声（过拟合），而不是拟合预期的输出。

权衡

偏差与方差的权衡是这两种错误之间的一个平衡。具有高偏差的模型对训练数据关注不足，过度简化模型，导致在训练数据和未见过的数据上性能都不好。另一方面，具有高方差的模型过多地关注训练数据并捕获噪声，导致在训练数据上表现良好但对新数据的泛化能力差。

平衡权衡

• 模型复杂性：增加模型的复杂性通常会降低偏差并增加方差。相反，降低复杂性会增加偏差并减少方差。关键是找到一个正确的平衡，使偏差和方差都最小化。

• 训练数据：训练数据的数量和质量可以影响这种权衡。更多的数据可以帮助降低方差而不增加偏差。同时，确保训练数据能代表现实世界情景可以减少偏差。

• 正则化：像L1和L2正则化这样的技术被用来对模型添加惩罚，目标是在不显著增加偏差的情况下减少方差。

例子

• 线性回归：简单的线性回归可能有高偏差但低方差。它假设一个线性关系，这可能过于简单。

• 决策树：这些倾向于有低偏差和高方差。它们可以捕获复杂的关系，但可能会过度拟合数据。

• 随机森林：通过结合多个决策树，随机森林旨在在保持相对较低的偏差的同时减少方差。

代码

创建一个完整的Python示例来说明偏差-方差权衡涉及多个步骤。我们将使用一个合成的数据集为了简洁和清晰。展示将包括：

1. 生成一个合成数据集。
2. 将不同的模型应用于这个数据集以说明欠拟合（高偏差）和过拟合（高方差）。
3. 绘制结果以可视化权衡。

在这个例子中，我将使用一个简单的多项式数据集，我们将尝试拟合不同复杂性（多项式度数）的线性回归模型。我们将使用numpy、matplotlib用于绘图，scikit-learn用于机器学习模型。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
np.random.seed(0)
X = np.random.normal(0, 1, 100)
y = X - 2 * (X ** 2) + np.random.normal(0, 0.1, 100)
X = X[:, np.newaxis]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
degrees = [1, 4, 15]
train_errors = []
test_errors = []
for degree in degrees:
    model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
    model.fit(X_train, y_train)
    
    train_predictions = model.predict(X_train)
    test_predictions = model.predict(X_test)
    
    train_errors.append(mean_squared_error(y_train, train_predictions))
    test_errors.append(mean_squared_error(y_test, test_predictions))
plt.figure(figsize=(10, 6))
plt.plot(degrees, train_errors, label='Train Error')
plt.plot(degrees, test_errors, label='Test Error')
plt.yscale('log')
plt.xlabel('Polynomial Degree')
plt.ylabel('Mean Squared Error')
plt.title('Bias-Variance Tradeoff')
plt.legend()
plt.show()

解释：

1. 合成数据：数据集是一个带有一些噪声的简单多项式。
2. 模型复杂度：模型中多项式特征的度数代表复杂度。

• 一个度数为1的多项式（线性模型）可能会导致数据欠拟合（高偏差）。
• 一个度数为15的多项式可能会导致数据过拟合（高方差）。

1. 误差测量：均方误差被用来量化训练和测试数据的误差。
2. 绘图：该图将显示误差如何随模型复杂度变化。理想情况下，训练误差随复杂度的增加而减少，但测试误差会先减少然后增加，证明了权衡。

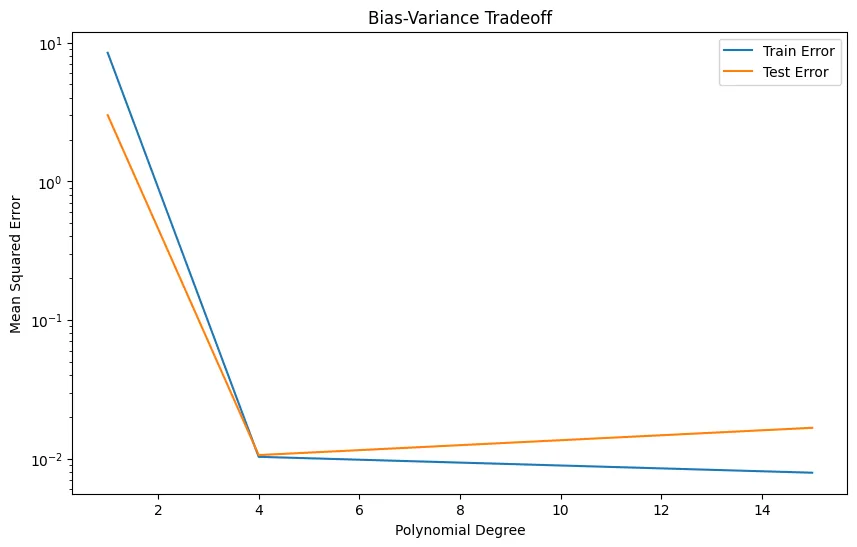
你可以在安装了必要库（numpy, matplotlib, scikit-learn）的Python环境中运行这段代码。此示例将清晰地展示机器学习背景下的偏差-方差权衡。

结论

偏差-方差权衡在机器学习中是至关重要的，因为它有助于开发出能够很好地推广到新的、未见过的数据的模型。它需要仔细的平衡、对问题领域的理解以及正确的算法和技术的选择。掌握这一概念可以导致创建出稳健、高效和准确的预测模型。