我们为什么需要深度强化学习？

Q-learning是一个适用于具有离散动作空间和限制观测空间环境的实际解决方案，但它难以很好地扩展到更复杂的环境中。的确，创建一个Q表需要定义动作空间和观测空间。

以自动驾驶为例，观测空间由摄像头视频流和其他传感器输入派生出的无限种可能的配置组成。另一方面，动作空间包括了广泛的方向盘位置范围以及对刹车和加速器施加的不同程度的力。

即便我们理论上可以将动作空间离散化，但是实际应用中可能状态和行动的巨大数量，导致了一个不切实际的Q表。

在庞大而复杂的状态-动作空间中寻找最优动作需要强大的函数逼近算法，而神经网络正是此类算法。在深度强化学习中，神经网络被用作Q表的替代物，提供了一种有效解决由大型状态空间带来的维度诅咒的方案。此外，我们不需要明确定义观测空间。

深度Q网络和回放缓冲区

DQN并行使用两种类型的神经网络：首先是用于Q值预测和决策的“在线”网络。另一方面，“目标”网络被用来创建稳定的Q目标，以通过损失函数评估在线网络的表现。

与Q-learning类似，DQN智能体通过两个函数定义：act和update。

act

act函数使用一个以Q值为基础的epsilon-贪婪策略，这些Q值由在线神经网络估算。换句话说，智能体会选择与给定状态的最大预测Q值对应的动作，并有一定概率随机行动。

你可能记得Q-learning在每一步之后更新其Q表，然而，在深度学习中，通常通过批量输入的梯度下降计算更新。

因此，DQN在回放缓冲区存储经验（包含状态、动作、奖励、下一状态、完成标志的元组）。为了训练网络，我们将从这个缓冲区采样一批经验，而不是仅使用最后的经验。

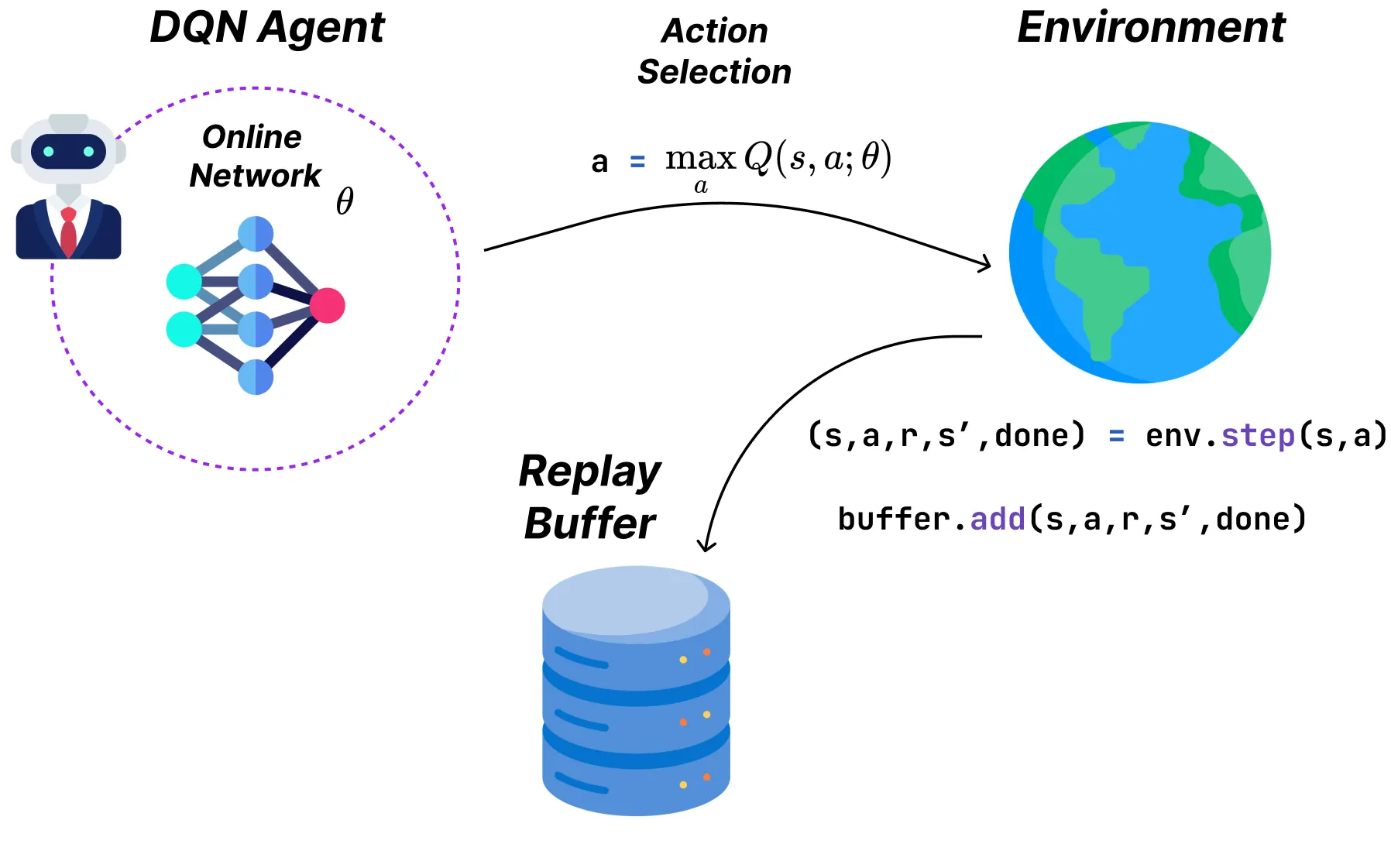
这里是基于JAX的DQN行动选择部分的实现：

class DQN():
    def __init__(
        self,
        model: hk.Transformed,
        discount: float,
        n_actions: int,
    ) -> None:
        self.model = model
        self.discount = discount
        self.n_actions = n_actions
    @partial(jit, static_argnums=(0))
    def act(
        self,
        key: random.PRNGKey,
        online_net_params: dict,
        state: jnp.ndarray,
        epsilon: float,
    ):
        def _random_action(subkey):
            return random.choice(subkey, jnp.arange(self.n_actions))
        def _forward_pass(_):
            q_values = self.model.apply(online_net_params, None, state)
            return jnp.argmax(q_values)
        explore = random.uniform(key) < epsilon
        key, subkey = random.split(key)
        action = lax.cond(
            explore,
            _random_action,
            _forward_pass,
            operand=subkey,
        )
        return action, subkey

这段代码的唯一微妙之处在于，model属性通常不包含任何内部参数，正如在PyTorch或TensorFlow这样的框架中常见的。

在这里，模型是一个代表我们架构的前向传播的函数，但是可变的权重是外部存储并作为参数传递的。这就解释了为什么我们能够在将self参数作为静态传递时使用静态传递（模型作为无状态与其他类属性一样）。

更新

更新函数负责训练网络。它基于时序差异(TD)误差计算均方误差(MSE)损失：

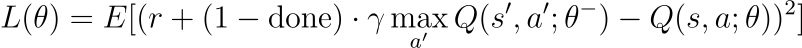
在这个损失函数中，θ表示在线网络的参数，θ−表示目标网络的参数。目标网络的参数每隔N步基于在线网络的参数进行设置，类似于一个检查点（N是一个超参数）。

这种参数分离（用θ表示当前的Q值，用θ−表示目标Q值）对于稳定训练至关重要。

使用相同的参数对于两者将类似于瞄准一个移动的目标，因为对网络的更新将会立刻改变目标值。通过定期更新θ−（即，固定这些参数一定数量的步骤），我们确保在在线网络继续学习的同时有稳定的Q目标。

最后，（1-done）这个项对终结状态的目标进行了调整。实际上，当一个剧情结束时（也就是‘done’等于1），就没有下一个状态了。因此，下一个状态的Q值被设为0。

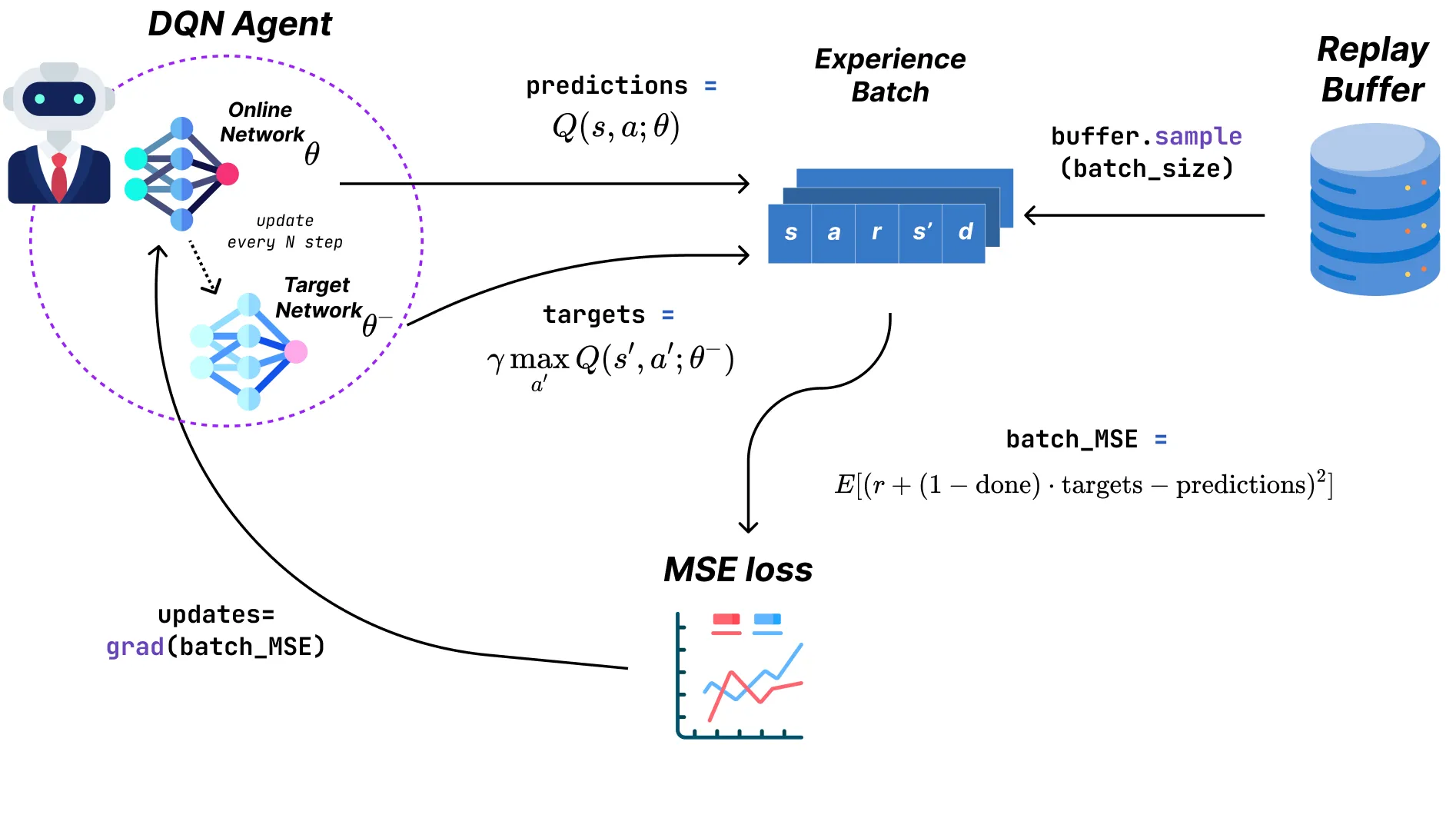
对DQN的更新函数的实现稍微复杂一些，让我们分解一下：

• 首先，_loss_fn函数实现了之前为单个经验描述的平方误差。
• 接着，_batch_loss_fn作为_loss_fn的封装，并用vmap装饰它，将损失函数应用于一批经验。然后我们返回这批经验的平均误差。
• 最后，update充当我们损失函数的最后一层，计算它相对于在线网络参数、目标网络参数和一批经验的梯度。然后我们使用Optax（一个通常用于优化的JAX库）来执行优化器步骤并更新在线参数。

@partial(jit, static_argnames=("self", "optimizer"))
def update(
    self,
    online_net_params: dict,
    target_net_params: dict,
    optimizer: optax.GradientTransformation,
    optimizer_state: jnp.ndarray,
    experiences: dict[
        str : jnp.ndarray
    ],  # states, actions, next_states, dones, rewards
):
    @jit
    def _batch_loss_fn(
        online_net_params: dict,
        target_net_params: dict,
        states: jnp.ndarray,
        actions: jnp.ndarray,
        rewards: jnp.ndarray,
        next_states: jnp.ndarray,
        dones: jnp.ndarray,
    ):
        # vectorize the loss over states, actions, rewards, next_states and done flags
        @partial(vmap, in_axes=(None, None, 0, 0, 0, 0, 0))
        def _loss_fn(
            online_net_params,
            target_net_params,
            state,
            action,
            reward,
            next_state,
            done,
        ):
            target = reward + (1 - done) * self.discount * jnp.max(
                self.model.apply(target_net_params, None, next_state),
            )
            prediction = self.model.apply(online_net_params, None, state)[action]
            return jnp.square(target - prediction)
        return jnp.mean(
            _loss_fn(
                online_net_params,
                target_net_params,
                states,
                actions,
                rewards,
                next_states,
                dones,
            ),
            axis=0,
        )
    loss, grads = value_and_grad(_batch_loss_fn)(
        online_net_params, target_net_params, **experiences
    )
    updates, optimizer_state = optimizer.update(grads, optimizer_state)
    online_net_params = optax.apply_updates(online_net_params, updates)
    return online_net_params, optimizer_state, loss

请注意，与回放缓冲区类似，模型和优化器是纯函数，用于修改外部状态。以下这行代码很好地说明了这个原理：

updates, optimizer_state = optimizer.update(grads, optimizer_state)

这也解释了为什么我们可以使用单一模型来同时作为在线网络和目标网络，因为参数是被外部存储和更新的。

# target network predictions
self.model.apply(target_net_params, None, state)
# online network predictions
self.model.apply(online_net_params, None, state)

对于上下文，我们在本文中使用的模型是多层感知器，定义如下：

N_ACTIONS = 2
NEURONS_PER_LAYER = [64, 64, 64, N_ACTIONS]
online_key, target_key = vmap(random.PRNGKey)(jnp.arange(2) + RANDOM_SEED)
@hk.transform
def model(x):
    # simple multi-layer perceptron
    mlp = hk.nets.MLP(output_sizes=NEURONS_PER_LAYER)
    return mlp(x)
online_net_params = model.init(online_key, jnp.zeros((STATE_SHAPE,)))
target_net_params = model.init(target_key, jnp.zeros((STATE_SHAPE,)))
prediction = model.apply(online_net_params, None, state)

回放缓冲区

现在让我们后退一步，仔细看看回放缓冲区（replay buffers）。它们在强化学习中因为多种原因而被广泛使用：

• 泛化：通过从回放缓冲区中采样，我们打乱连续经验之间的相关性，从而打破了它们的顺序。这样，我们避免了对特定经验序列的过度拟合。
• 多样性：由于采样不限于近期的经验，我们通常观察到在更新中的方差更低并防止对最新经验的过度拟合。
• 提高样本效率：每个经验可以从缓冲区中被多次采样，使得模型能够从个别经验中学习更多。

最后，我们可以对重播缓冲区使用几种采样方案：

• 均匀采样：经验被均匀随机地采样。这种类型的采样易于实现，并且允许模型独立于它们被收集的时间步从经验中学习。
• 优先级采样：这一类别包括了不同的算法，如优先级体验回放（“PER”，Schaul 等人，2015年）或梯度经验回放（“GER”，Lahire 等人，2022年）。这些方法试图根据一些与它们的“学习潜力”相关的度量来优先选择经验（对于PER来讲是TD误差的幅度，对于GER来讲是经验梯度的范数）。

为了简化，我们将在本文中实现一个均匀回放缓冲区。

正如承诺，均匀回放缓冲区实现起来相当容易，然而，使用JAX和函数式编程相关的有一些复杂性。一如既往，我们必须使用纯函数，这些函数无副作用。换句话说，我们不允许将缓冲区定义为具有可变内部状态的类实例。

相反，我们初始化一个buffer_state字典，它将键映射到具有预定义形状的空数组，因为当使用jit编译代码到XLA时，JAX要求数组大小是常数。

buffer_state = {
    "states": jnp.empty((BUFFER_SIZE, STATE_SHAPE), dtype=jnp.float32),
    "actions": jnp.empty((BUFFER_SIZE,), dtype=jnp.int32),
    "rewards": jnp.empty((BUFFER_SIZE,), dtype=jnp.int32),
    "next_states": jnp.empty((BUFFER_SIZE, STATE_SHAPE), dtype=jnp.float32),
    "dones": jnp.empty((BUFFER_SIZE,), dtype=jnp.bool_),
}

我们将使用一个 UniformReplayBuffer 类来与缓冲状态进行交互。这个类有两个方法：

• add：解包体验元组，并将其组成部分映射到特定索引。idx = idx % self.buffer_size 确保当缓冲区满时，添加新体验会覆盖旧体验。
• sample：从均匀随机分布中抽样一系列随机索引。序列的长度由 batch_size 设置，而索引的范围是 [0, current_buffer_size-1]。这确保了当缓冲区还没有满时，我们不会抽样空数组。最后，我们结合使用 JAX 的 vmap 和 tree_map 来返回一批体验数据。

class UniformReplayBuffer():
    def __init__(
        self,
        buffer_size: int,
        batch_size: int,
    ) -> None:
        self.buffer_size = buffer_size
        self.batch_size = batch_size
        
    @partial(jit, static_argnums=(0))
    def add(
        self,
        buffer_state: dict,
        experience: tuple,
        idx: int,
    ):
        state, action, reward, next_state, done = experience
        idx = idx % self.buffer_size
        buffer_state["states"] = buffer_state["states"].at[idx].set(state)
        buffer_state["actions"] = buffer_state["actions"].at[idx].set(action)
        buffer_state["rewards"] = buffer_state["rewards"].at[idx].set(reward)
        buffer_state["next_states"] = buffer_state["next_states"].at[idx].set(next_state)
        buffer_state["dones"] = buffer_state["dones"].at[idx].set(done)
        return buffer_state
    @partial(jit, static_argnums=(0))
    def sample(
        self,
        key: random.PRNGKey,
        buffer_state: dict,
        current_buffer_size: int,
    ):
        
        @partial(vmap, in_axes=(0, None)) # iterate over the indexes
        def sample_batch(indexes, buffer):
            """
            For a given index, extracts all the values from the buffer
            """
            return tree_map(lambda x: x[indexes], buffer)
        key, subkey = random.split(key)
        indexes = random.randint(
            subkey,
            shape=(self.batch_size,),
            minval=0,
            maxval=current_buffer_size,
        )
        experiences = sample_batch(indexes, buffer_state)
        
        return experiences, subkey

将CartPole环境翻译成JAX

现在我们的DQN代理已经准备好进行训练，我们将迅速实现一个向量化的CartPole环境。CartPole是一个控制环境，拥有一个较大的连续观测空间，这使得它适合测试我们的DQN。

这个过程相当直接，我们重用了大部分OpenAI的Gymnasium实现，同时确保我们使用JAX数组和lax控制流，而不是Python或Numpy的选择，例如：

# Python implementation
force = self.force_mag if action == 1 else -self.force_mag
# Jax implementation
force = lax.select(jnp.all(action) == 1, self.force_mag, -self.force_mag)            )
# Python
costheta, sintheta = math.cos(theta), math.sin(theta)
# Jax
cos_theta, sin_theta = jnp.cos(theta), jnp.sin(theta)
# Python
if not terminated:
  reward = 1.0
...
else: 
  reward = 0.0
# Jax
reward = jnp.float32(jnp.invert(done))

编写高效训练循环的JAX方法

我们实现DQN的最后部分是训练循环。

首次接触时，rollout函数可能看起来令人生畏，但其复杂性大部分只是在语法上的，因为我们已经覆盖了大多数构建块。这里是一个伪代码走查：

1. Initialization:
  * Create empty arrays that will store the states, actions, rewards 
    and done flags for each timestep. Initialize the networks and optimizer
    with dummy arrays.
  * Wrap all the initialized objects in a val tuple
2. Training loop (repeat for i steps):
  * Unpack theval tuple
  * (Optional) Decay epsilon using a decay function
  * Take an action depending on the state and model parameters
  * Perform an environment step and observe the next state, reward 
    and done flag
  * Create an experience tuple (state, action, reward, new_state, done)
    and add it to the replay buffer
  * Sample a batch of experiences depending on the current buffer size
    (i.e. sample only from experiences that have non-zero values)
  * Update the model parameters using experience batch
  * Every N steps, update the target network's weights 
    (set target_params = online_params)
  * Store the experience's values for the current episode and return 
    the updated `val` tuple

def DeepRlRollout(
    timesteps: int,
    random_seed: int,
    target_net_update_freq: int,
    model: hk.Transformed,
    optimizer: optax.GradientTransformation,
    buffer_state: dict,
    agent: BaseDeepRLAgent,
    env: BaseControlEnv,
    replay_buffer: BaseReplayBuffer,
    state_shape: int,
    buffer_size: int,
    batch_size: int,
    epsilon_decay_fn: Callable,
    epsilon_start: float,
    epsilon_end: float,
    decay_rate: float,
):
    @loop_tqdm(timesteps) # progress bar display
    @jit
    def _fori_body(i: int, val: tuple):
        (
            model_params,
            target_net_params,
            optimizer_state,
            buffer_state,
            action_key,
            buffer_key,
            env_state,
            all_actions,
            all_obs,
            all_rewards,
            all_done,
            losses,
        ) = val
        state, _ = env_state
        epsilon = epsilon_decay_fn(epsilon_start, epsilon_end, i, decay_rate)
        action, action_key = agent.act(action_key, model_params, state, epsilon)
        env_state, new_state, reward, done = env.step(env_state, action)
        experience = (state, action, reward, new_state, done)
        buffer_state = replay_buffer.add(buffer_state, experience, i)
        current_buffer_size = jnp.min(jnp.array([i, buffer_size]))
        experiences_batch, buffer_key = replay_buffer.sample(
            buffer_key,
            buffer_state,
            current_buffer_size,
        )
        model_params, optimizer_state, loss = agent.update(
            model_params,
            target_net_params,
            optimizer,
            optimizer_state,
            experiences_batch,
        )
        # update the target parameters every ``target_net_update_freq`` steps
        target_net_params = lax.cond(
            i % target_net_update_freq == 0,
            lambda _: model_params,
            lambda _: target_net_params,
            operand=None,
        )
        all_actions = all_actions.at[i].set(action)
        all_obs = all_obs.at[i].set(new_state)
        all_rewards = all_rewards.at[i].set(reward)
        all_done = all_done.at[i].set(done)
        losses = losses.at[i].set(loss)
        val = (
            model_params,
            target_net_params,
            optimizer_state,
            buffer_state,
            action_key,
            buffer_key,
            env_state,
            all_actions,
            all_obs,
            all_rewards,
            all_done,
            losses,
        )
        return val
    init_key, action_key, buffer_key = vmap(random.PRNGKey)(jnp.arange(3) + random_seed)
    env_state, _ = env.reset(init_key)
    all_actions = jnp.zeros([timesteps])
    all_obs = jnp.zeros([timesteps, state_shape])
    all_rewards = jnp.zeros([timesteps], dtype=jnp.float32)
    all_done = jnp.zeros([timesteps], dtype=jnp.bool_)
    losses = jnp.zeros([timesteps], dtype=jnp.float32)
    model_params = model.init(init_key, jnp.zeros((state_shape,)))
    target_net_params = model.init(action_key, jnp.zeros((state_shape,)))
    optimizer_state = optimizer.init(model_params)
    val_init = (
        model_params,
        target_net_params,
        optimizer_state,
        buffer_state,
        action_key,
        buffer_key,
        env_state,
        all_actions,
        all_obs,
        all_rewards,
        all_done,
        losses,
    )
    vals = lax.fori_loop(0, timesteps, _fori_body, val_init)
    return vals

我们现在可以运行 DQN 20000步，并观察性能表现。经过大约45个剧集后，代理成功地获得了不错的性能，连续平衡杆超过100步。

绿色条表示代理成功地平衡杆超过200步，解决了环境问题。特别地，在第51个剧集，代理创下了393步的记录。

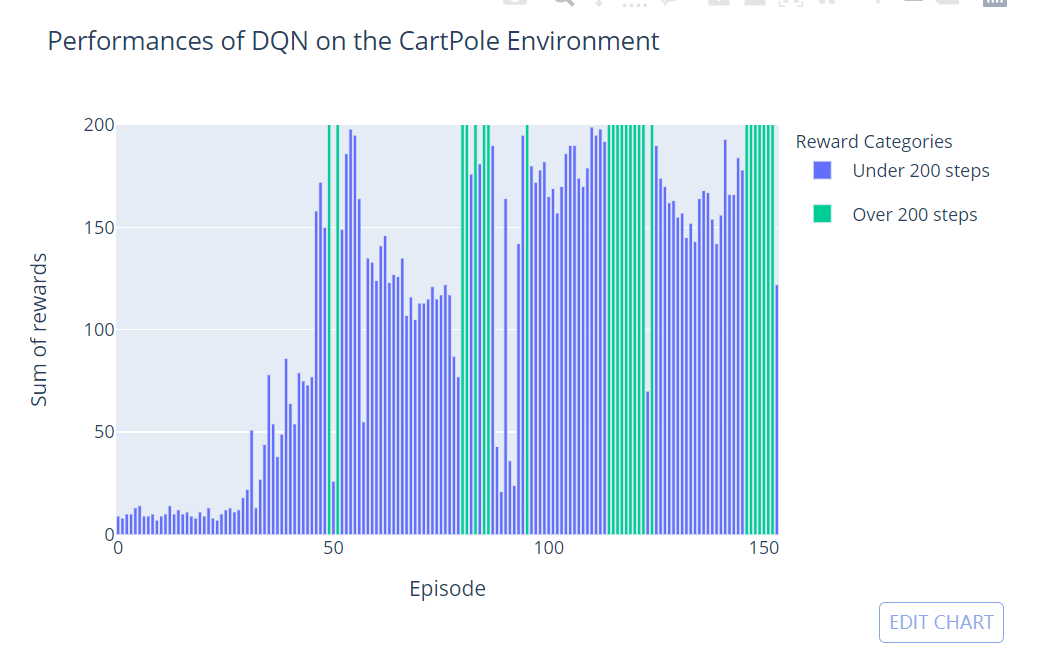
20,000个训练步骤仅用了一秒多一点的时间就执行完毕，速度是每秒15.807步（在单个CPU上）！

这些表现暗示了JAX令人印象深刻的扩展能力，使实践者能够在最小的硬件需求下运行大规模的并行实验。

Running for 20,000 iterations: 100%|██████████| 20000/20000 [00:01<00:00, 15807.81it/s]