介绍

傅里叶变换是一种数学工具，它能将信号从其原始域（通常是时间或空间）转换到频率域的表示中。简而言之，它将函数分解成振荡函数，揭示了原始信号的频谱。这种转换在各个领域都至关重要，包括信号处理、物理和工程学，用于分析信号中存在的频率。在自然语言处理（NLP）中的傅里叶变换是一个引人入胜且复杂的主题，将数学理论与人类语言的复杂性结合起来。本文将探讨傅里叶变换在NLP中的应用，从概念的介绍开始，接着讨论其在语言处理中的作用，并以其局限性和未来前景作为结束。

通过傅立叶变换的视角在自然语言处理（NLP）中，我们不仅可以看到文字的节奏，还能感受到语言的交响乐。

自然语言处理中的应用

1. 文本的信号处理类比：在NLP中，文本可以被类比为信号。文本中的单词或短语可以被视为贡献于文本整体意义（或信号）的‘频率’。傅立叶变换可以应用于分析这些频率，帮助识别文本中的模式、主题甚至情感。
2. 特征提取：傅立叶变换技术可以用来从文本数据中提取特征。通过分析单词或n-gram（文本样本中连续的n项序列）的频率，可以构建代表文本的数值形式的特征向量，这是许多机器学习算法的基本步骤。
3. 过滤和降噪：就像在信号处理中使用傅立叶变换来滤除噪声一样，在NLP中，它们可以帮助减少‘噪声’——文本数据中的无关或冗余信息。这个过程提高了喂入机器学习模型的数据的质量。
4. 时间序列分析：对于随时间演变的文本，如推文或新闻文章，可以应用傅立叶变换来分析时间上的趋势和模式。这种时间分析可以揭示诸如某个话题如何获得或失去流行度的洞见。

局限性和挑战

1. 语言的复杂性：人类语言天生比傅立叶变换分析的典型信号更加复杂。歧义、上下文依赖性和丰富的语言表达形式都构成了重大挑战。
2. 预处理需求：文本数据在应用傅立叶变换之前需要进行大量预处理（如标记化、词干提取、去除停用词），这可能会很消耗资源。
3. 语义意义丢失：傅立叶变换在识别模式上可能很有效，但它可能会忽略语义细微差别，因为转换更多地专注于元素的频率而非它们在上下文中的含义。

未来展望和结论

在NLP中应用傅立叶变换仍是一个不断发展的领域。随着计算能力和机器学习技术的进步，更能捕捉人类语言细微差别的复杂模型很可能会被开发出来。将傅立叶变换与其他NLP技术如自然语言理解（NLU）和上下文感知模型结合，可能会导致更强大和精确的语言处理工具的出现。

代码

创建一个完整的Python示例，展示在自然语言处理（NLP）中如何使用傅立叶变换涉及到几个步骤。我将指导你创建一个合成数据集，应用傅立叶变换，并使用图表进行结果的可视化。

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
from collections import Counter
import re
# Synthetic dataset
sentences = [
    "cat cat dog mouse",
    "dog mouse cat",
    "mouse cat dog cat",
    "cat cat cat dog",
    "dog mouse"
]
# Preprocessing: Tokenize and create a flat list of words
words = [word for sentence in sentences for word in re.split(r'\W+', sentence)]
# Calculate word frequencies
word_freq = Counter(words)
# Frequencies to be transformed
frequencies = list(word_freq.values())
# Apply Fourier Transform
transformed = fft(frequencies)
# Frequencies for plotting (ignoring negative frequencies)
freqs = np.fft.fftfreq(len(frequencies))
mask = freqs >= 0
# Plot original frequencies
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.bar(word_freq.keys(), word_freq.values())
plt.title('Original Word Frequencies')
plt.xlabel('Words')
plt.ylabel('Frequency')
# Plot Fourier Transform
plt.subplot(1, 2, 2)
plt.bar(freqs[mask], np.abs(transformed)[mask])
plt.title('Fourier Transform')
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
plt.show()

• 预处理：句子被分词以创建一个单词列表。
• 词频计算：使用Counter计算每个单词的出现次数。
• 傅里叶变换：使用scipy的fft函数来转换单词频率。
• 可视化：创建两个图表；一个显示原始的单词频率，另一个显示傅里叶变换的结果。

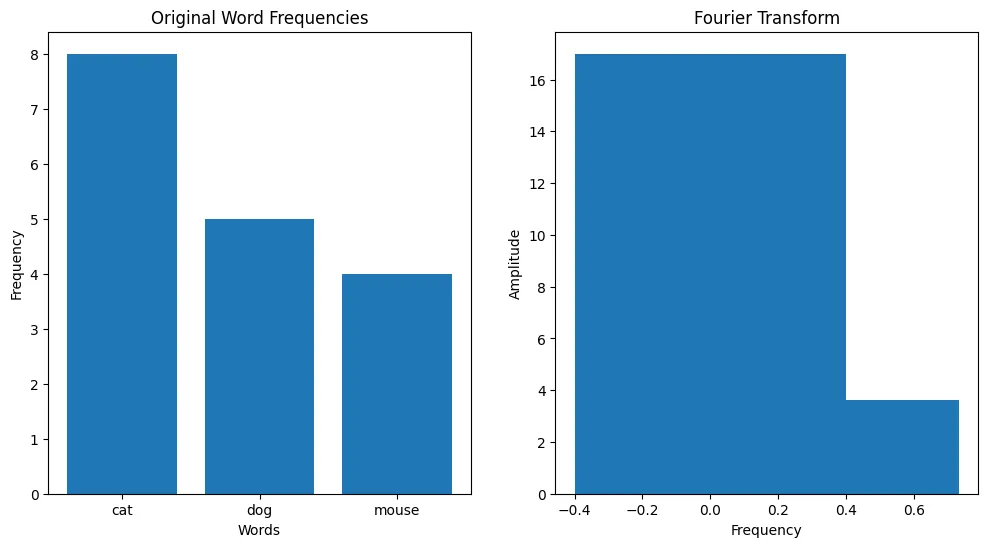
这段代码简单展示了如何将傅里叶变换应用于自然语言处理中的词频分析。在现实世界的场景中，更复杂的数据和预处理工作是必需的。此外，在自然语言处理的背景下解释傅里叶变换的结果可能是具有挑战性的，并且通常需要更高级的分析技术。

结论

总之，尽管傅里叶变换在分析文本数据方面提供了独特的视角，但其在自然语言处理中的全部潜力尚未被发掘。这种数学方法与复杂的人类语言世界的融合，为自然语言处理的未来带来了令人兴奋的可能性。