介绍

在不断发展的机器学习领域中，源于控制论的必要多样性法则提供了对智能系统开发和有效性的深刻洞察。这一法则最初由W. Ross Ashby提出，它规定一个系统控制其环境的能力与其响应的复杂性成正比。在机器学习的背景下，这意味着算法处理和适应现实世界数据多样性的能力。本文探讨了必要多样性法则在机器学习中的影响，着重指出其在设计自适应、稳健和高效模型中的重要性。

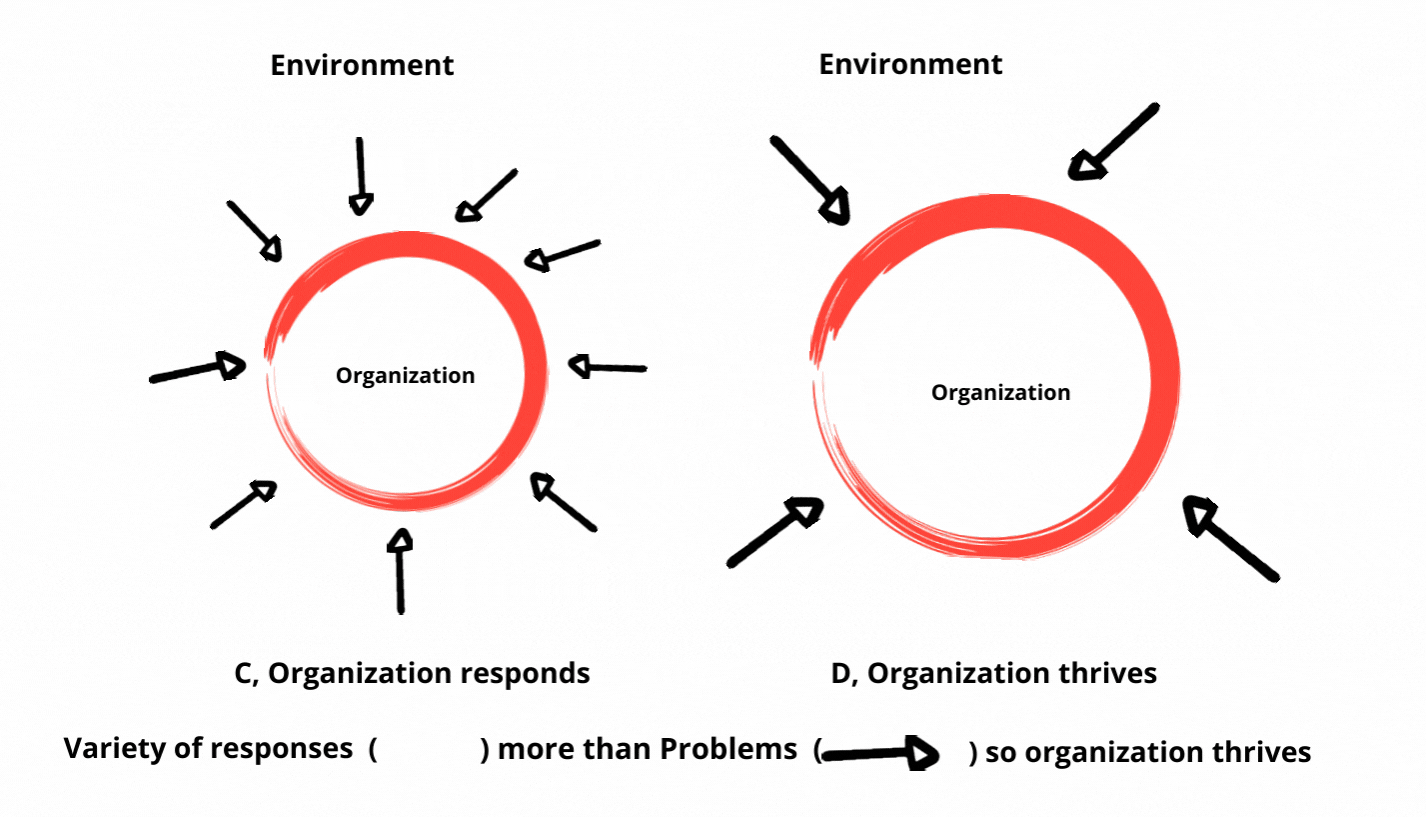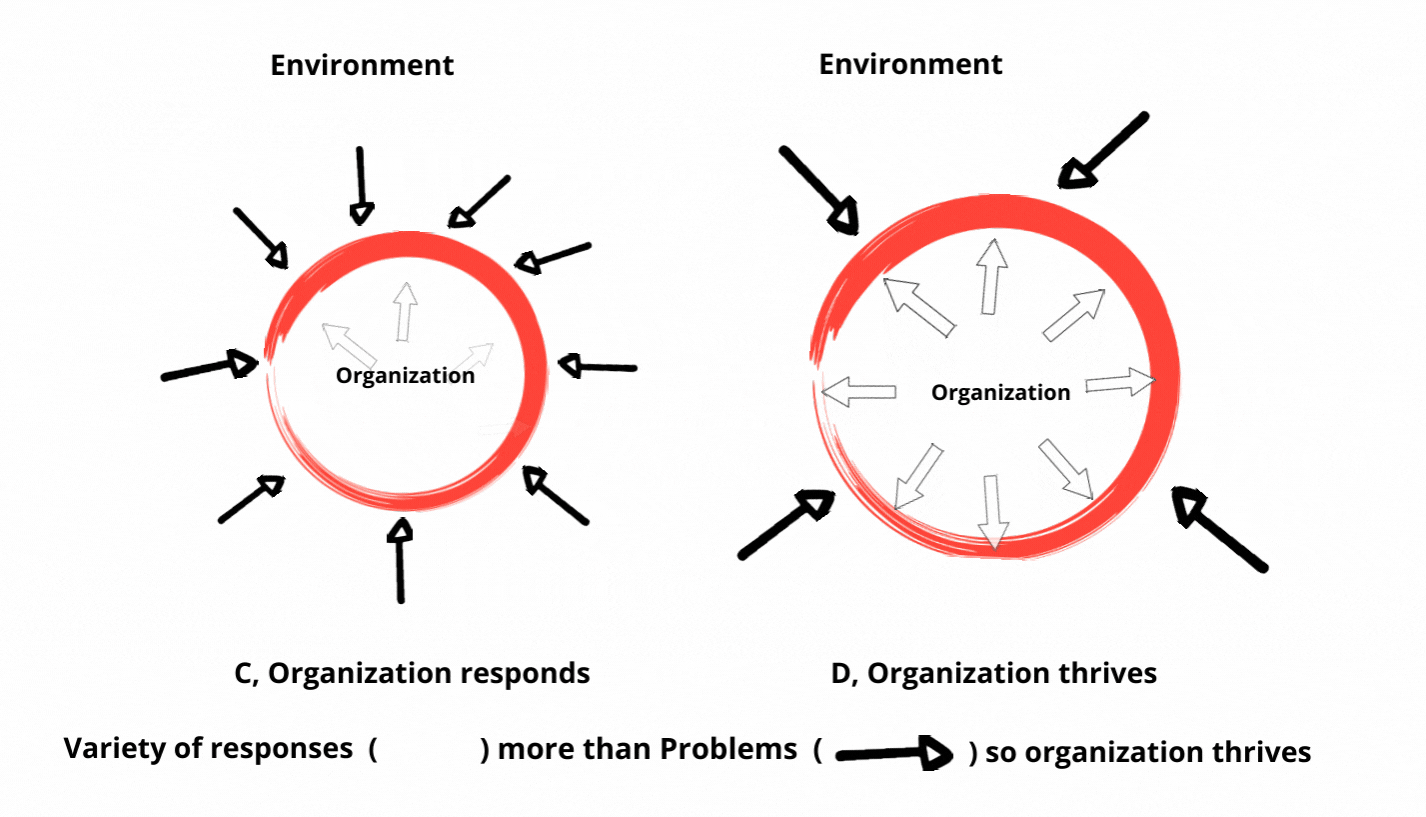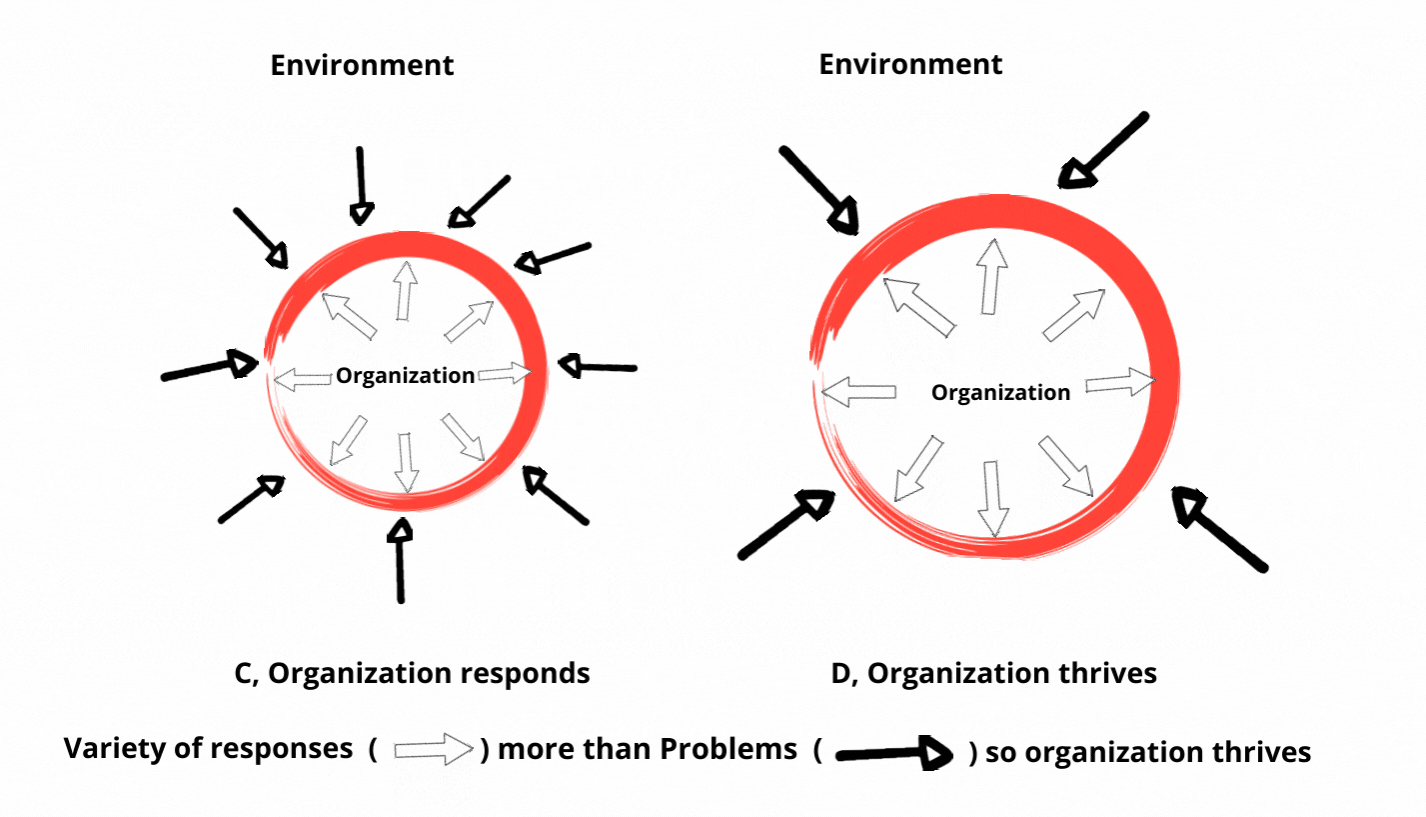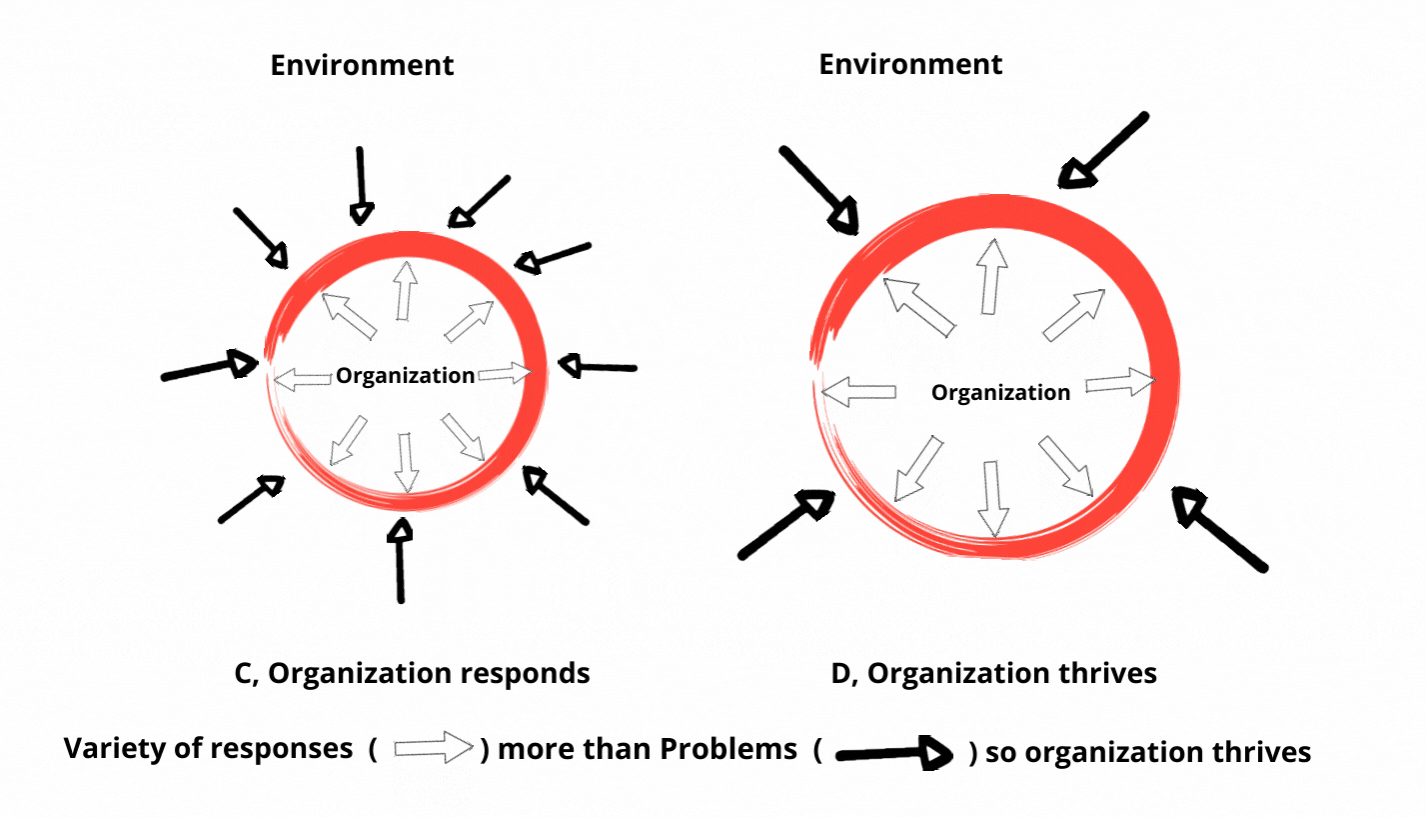
理解机器学习中的必要多样性法则

必要多样性法则的核心是处理系统内部复杂性与其面临的外部挑战之间的关系。在机器学习中，这一概念体现在算法从多样化的数据输入中学习的能力。数据越多样化和全面，学习算法就越适应性强和有效。这一原则突出了训练数据集的多样性和捕捉现实世界情景细微差别的模型复杂性的需求。

自适应学习和模型复杂性

机器学习模型往往负责解析数据中复杂的模式，需要与数据本身的复杂性相匹配的复杂性水平。例如，深度学习架构通过采用多层神经元来模拟复杂关系，体现了必要多样性法则。这些架构从庞大的数据集中自适应性地学习，不断调整它们的参数以更好地适应潜在的数据分布。

平衡复杂性和过拟合

遵守必要多样性法则的一个关键挑战是避免过拟合，即模型对训练数据的调整过于精细，以至于无法泛化到新数据上。这种现象类似于系统有过多的内部多样性，超过了有效处理外部环境所需要的多样性。采用正则化技术、交叉验证和审慎的模型选择是保持这种平衡的关键策略。

数据多样性的作用

必要多样性法则还强调了数据多样性的重要性。在有限或有偏见的数据集上训练的机器学习模型可能不具备处理多样真实世界情境的必要多样性。确保数据多样性符合Ashby的法则，通过为模型装备更广泛的情景范围，提高它们的预测准确性和泛化能力。

在现实世界情景中的应用

在实践中，必要多样性法则在众多应用中具有相关性。在自动驾驶汽车中，机器学习模型必须解释多种传感器输入以做出安全的驾驶决策。在医疗保健中，训练有素的模型可以更准确地诊断和预测患者结果。每个应用都展示了该法则的原理：模型的有效性取决于其反映其运行环境的复杂性和多样性的能力。

代码

要用Python演示必要多样性法则，我们将创建一个合成数据集，实施一个简单的机器学习模型，并可视化模型的复杂性与其处理多样化数据的能力之间的关系。我们将遵循以下步骤：

1. 生成合成数据集：我们将创建一个具有一定复杂度的数据集。
2. 实施机器学习模型：我们将使用不同复杂度的模型。
3. 训练和评估模型：评估每个模型在数据集上的表现如何。
4. 可视化结果：绘制模型的表现与其复杂性之间的关系。

为了这个演示的目的，我们将使用一个有着多项式关系的回归任务在输入和输出之间。我们将使用不同多项式度数的模型来代表不同的复杂性水平。

让我们开始编写这个演示的Python代码。

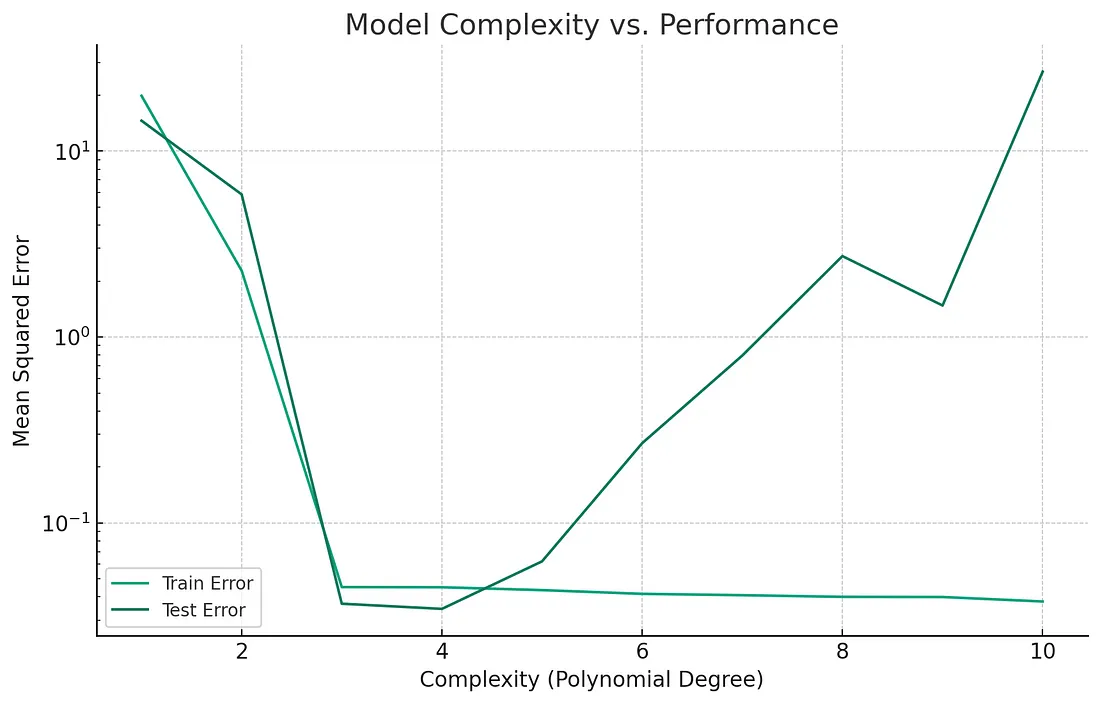
该图展示了机器学习模型的复杂性（以多项式次数表示）与其在训练集和测试集上的性能（通过均方误差衡量）之间的关系。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
# Step 1: Generate a Synthetic Dataset
np.random.seed(0)
X = np.random.normal(0, 1, 100)
y = X**3 - 3*X**2 + 2*X + np.random.normal(0, 0.2, 100)
X = X[:, np.newaxis]
# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# Step 2 and 3: Implementing Models with Varying Complexities and Evaluating Them
degrees = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
train_errors = []
test_errors = []
for degree in degrees:
    model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
    model.fit(X_train, y_train)
    
    train_predictions = model.predict(X_train)
    test_predictions = model.predict(X_test)
    
    train_errors.append(mean_squared_error(y_train, train_predictions))
    test_errors.append(mean_squared_error(y_test, test_predictions))
# Step 4: Visualizing Results
plt.figure(figsize=(10, 6))
plt.plot(degrees, train_errors, label='Train Error')
plt.plot(degrees, test_errors, label='Test Error')
plt.xlabel('Complexity (Polynomial Degree)')
plt.ylabel('Mean Squared Error')
plt.title('Model Complexity vs. Performance')
plt.legend()
plt.yscale('log')
plt.show()

关键观察：

1. 低复杂度模型：对于低阶多项式（例如，一阶或二阶），我们在训练集和测试集上都观察到较高的误差。这表明这些模型太简单，无法捕捉数据的底层复杂性，这种现象被称为欠拟合。
2. 适当复杂度：在数据生成过程的真实复杂度附近（在这个案例中是三阶），训练误差和测试误差都最小化。这表明模型的复杂度很适合数据中存在的多样性。
3. 高复杂度模型：当模型复杂度超过数据的固有复杂度（高于三阶）时，训练误差会继续降低，表明模型非常适合训练数据。然而，测试误差在某个点之后开始增加。这是过拟合的经典迹象，其中模型对于数据来说太复杂，并开始学习训练集中的噪声而不是底层模式。

这次演示与必要多样性定律相符，显示出模型需要有一个与其所建模数据的复杂度相匹配的复杂度（响应的多样性）。过少的复杂度会导致欠拟合，而过多则导致过拟合。最佳状态是模型的复杂度刚好可以捕捉到数据中的基本模式，而不会被噪声或无关细节所影响。

结论

必要多样性定律在机器学习领域起着指导原则的作用，提醒从业者在模型复杂度与环境多样性之间的关键平衡。通过拥抱这一法则，机器学习可以继续进步，创建出不仅复杂和适应性强，而且稳健且适用于现实世界广泛和多样化挑战的模型。随着该领域的进步，该法则的洞察将在教导机器学习、适应和在不断变化的环境中做出决策的复杂性中保持着无价的价值。