介绍

Levenberg-Marquardt（LM）算法经常用于求解非线性最小二乘问题，它是两种最小化方法的结合：梯度下降法和高斯-牛顿法。LM算法最初是为解决非线性方程组开发的，但它在神经网络的训练中发现了重要的应用。Levenberg-Marquardt优化算法是一个复杂的技术，经常用于小数据集的神经网络训练中。本文将探讨Levenberg-Marquardt优化的基本原理、其在神经网络中的应用，以及它的优势和局限性。

Levenberg-Marquardt优化基础

数学基础

LM算法迭代更新模型的参数，以最小化成本函数，通常为预测输出与实际输出之间平方误差的总和。更新规则结合了梯度下降法和高斯-牛顿法的元素：

ErrorΔθ=(JTJ+λI)−1JTError

这里，Δθ代表参数的变化量，J是模型输出关于其参数的偏导数组成的雅可比矩阵，λ是一个阻尼因子，I是单位矩阵。

算法动力学

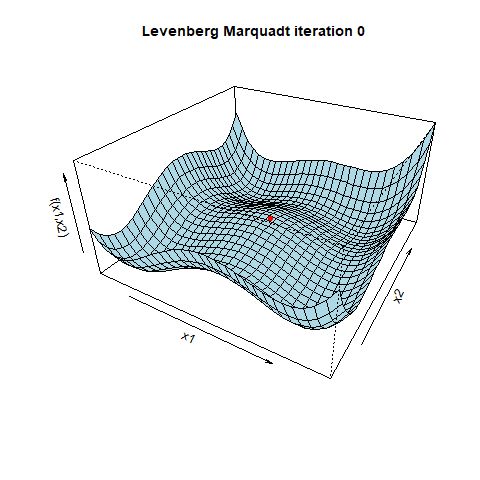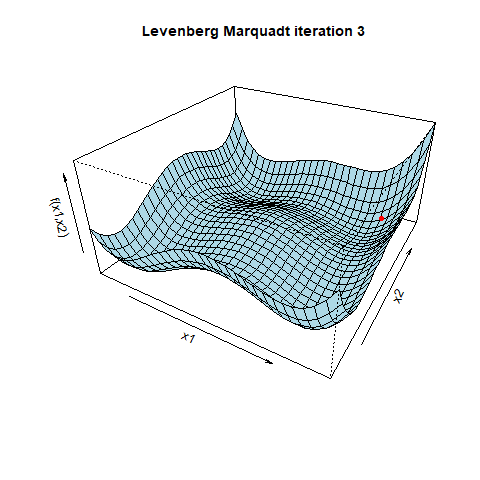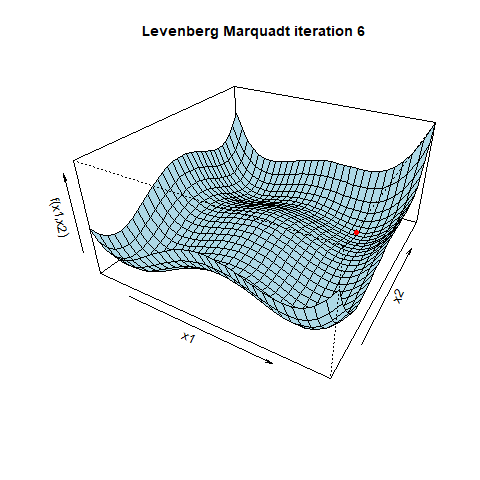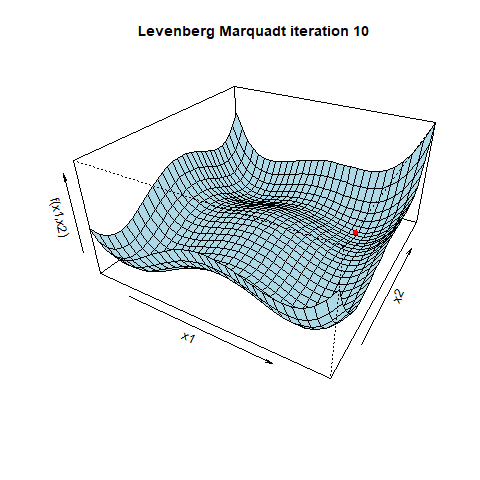
阻尼因子λ在算法中起着关键作用。当λ较高时，算法的行为更像梯度下降，采取小而可靠的步伐。随着λ的减小，算法采取了高斯-牛顿方法的特点，采取更大、更具侵略性的步骤。这种自适应行为有助于在神经网络复杂的错误景观中导航。

在神经网络中的应用

适用于小型数据集

LM优化对于较小的数据集特别有效。在这些场景下，算法可以快速收敛到一个好的解决方案，使其成为数据有限的应用。

训练动力学

在神经网络的训练过程中，LM优化有效地计算参数更新，导致可能比常规方法如使用梯度下降的反向传播更快地收敛。这在具有许多层或复杂架构的网络中尤其有价值。

优点

1. 快速收敛：LM算法可以比标准梯度下降方法更快地收敛，尤其是在接近解决方案的情景中。
2. 稳健性：它在高斯-牛顿方法的速度和梯度下降稳定性之间提供了良好的平衡。
3. 在小型数据集中效率：特别适用于数据有限的场景。

局限性

1. 存储密集型：需要计算和求逆雅可比矩阵的要求使其变得存储密集型，限制了其扩展到非常大型网络的可行性。
2. λ的调整：选择正确的阻尼因子可能具有挑战性，可能需要实验。
3. 对大型数据集效果较差：对于大型数据集，计算开销可能是一个显著的缺点。

代码

创建一个完整的Python实现Levenberg-Marquardt优化算法用于神经网络涉及几个步骤。我们将创建一个合成数据集，定义一个简单的神经网络，实施Levenberg-Marquardt优化算法，然后使用该算法训练网络。最后，我们将绘制结果以可视化性能。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import least_squares
# Step 1: Generate a Synthetic Dataset
np.random.seed(0)
x_data = np.linspace(-2, 2, 100)
y_data = 1.5 * np.sin(x_data * np.pi) + np.random.normal(0, 0.2, 100)
# Step 2: Define a Simple Neural Network
def neural_network(weights, x):
    # Simple neural network with one hidden layer
    w1, w2, b1, b2 = weights
    hidden = np.tanh(w1 * x + b1)
    return w2 * hidden + b2
def model(weights, x, y):
    return neural_network(weights, x) - y
# Initial weights
initial_weights = [1.0, 1.0, 0.0, 0.0]  # w1, w2, b1, b2
# Step 3: Levenberg-Marquardt Optimization
res = least_squares(model, initial_weights, args=(x_data, y_data), method='lm')
# Step 4: Training the Network
trained_weights = res.x
# Step 5: Plotting the Results
plt.figure(figsize=(10, 5))
# Plotting the synthetic dataset
plt.scatter(x_data, y_data, label='Synthetic Data')
# Plotting the model's predictions
y_pred = neural_network(trained_weights, x_data)
plt.plot(x_data, y_pred, color='red', label='NN Predictions')
plt.title('Neural Network Training with Levenberg-Marquardt Optimization')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

我们开始编写并执行这些步骤的代码吧。

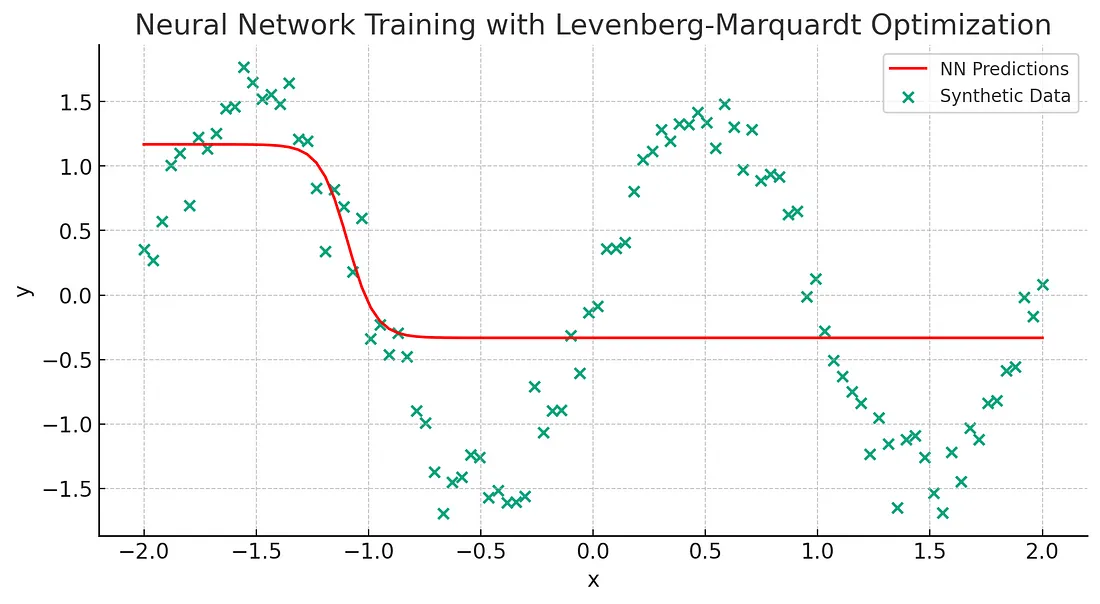
上述情节展示了使用 Levenberg-Marquardt 优化算法训练一个简单神经网络在一个合成数据集上的结果。数据集点（蓝色）遵循一个带有噪音的非线性函数，而神经网络的预测以红色表示。

结论

Levenberg-Marquardt 优化算法为训练神经网络提供了一种强大的技术，尤其是在数据有限的场景中。它在梯度下降的强大性和高斯-牛顿方法的速度之间平衡的能力，使它成为一个有价值的工具。然而，它内存密集的本质和在处理大型数据集时效果不佳的限制，限制了它的应用性。未来在优化 LM 算法方面的研究和发展可能会扩大它在迅速发展的神经网络领域的实用性。