简介

Dropout是深度学习中用于防止过拟合的正则化技术。这个概念由Hinton等人在2012年的一篇论文中提出，自那以后，它已经成为神经网络领域，特别是在训练深层网络的主要技术。

理解过拟合

要理解dropout的重要性，首先需要理解过拟合。过拟合发生在模型对训练数据学得太好，以至于失去了对新的、未见过的数据的泛化能力。这是深度学习中常见的问题，因为神经网络有学习复杂模式的高容量。

Dropout技术

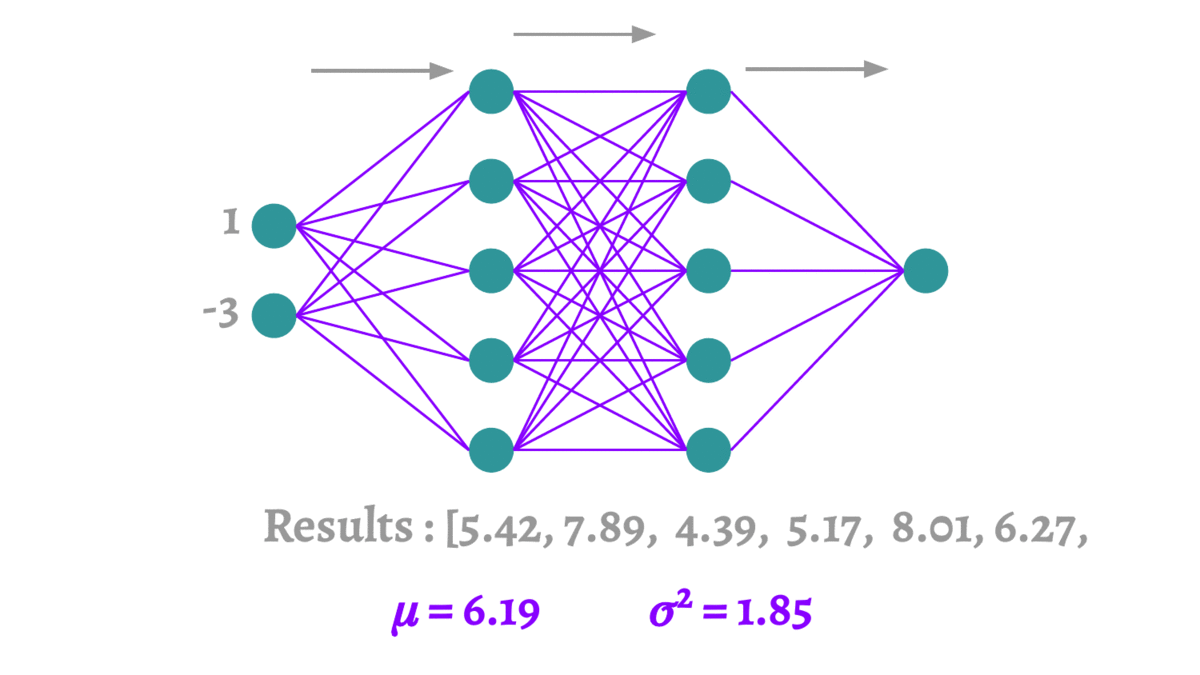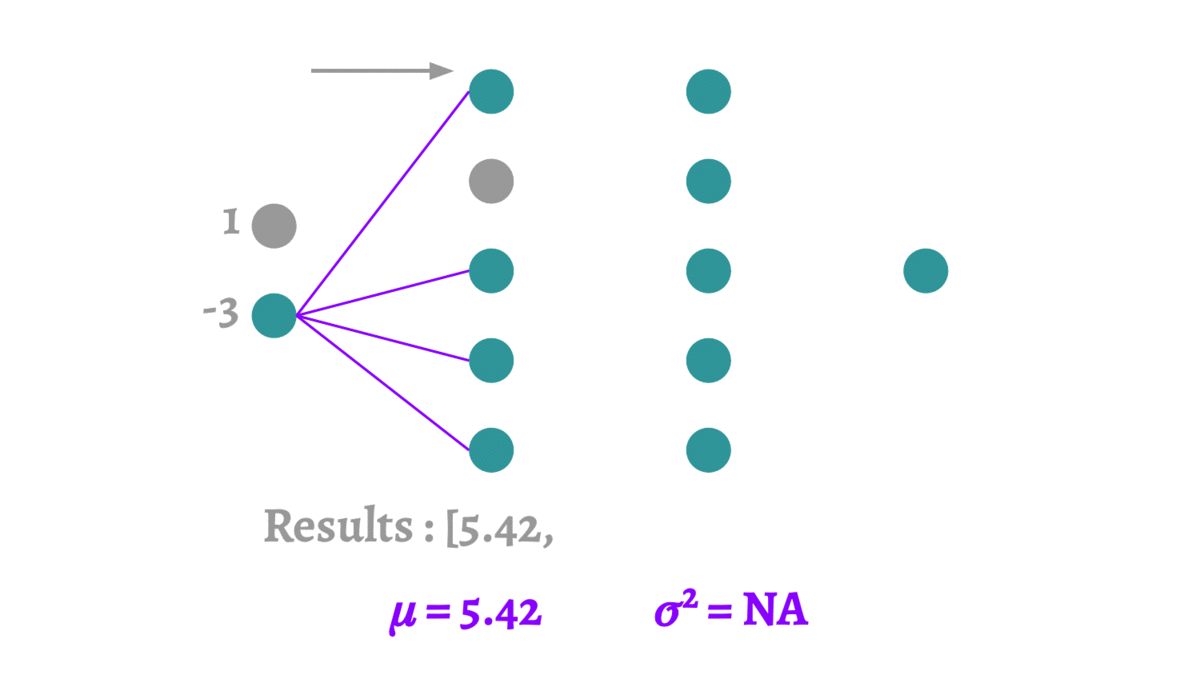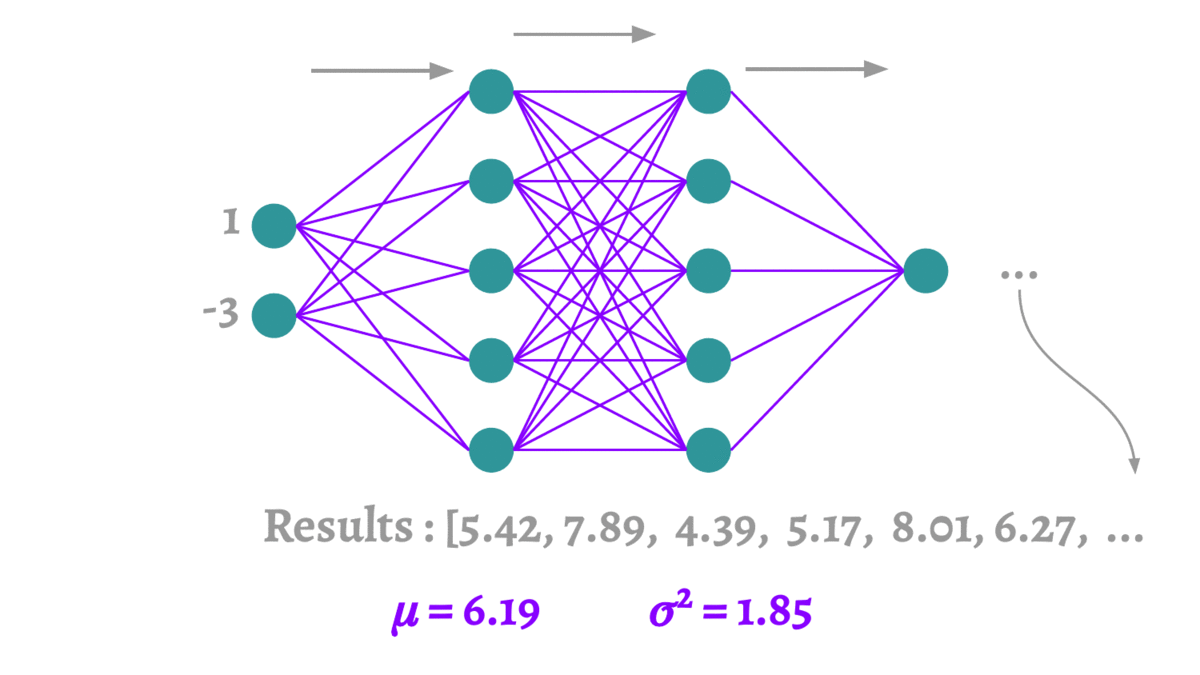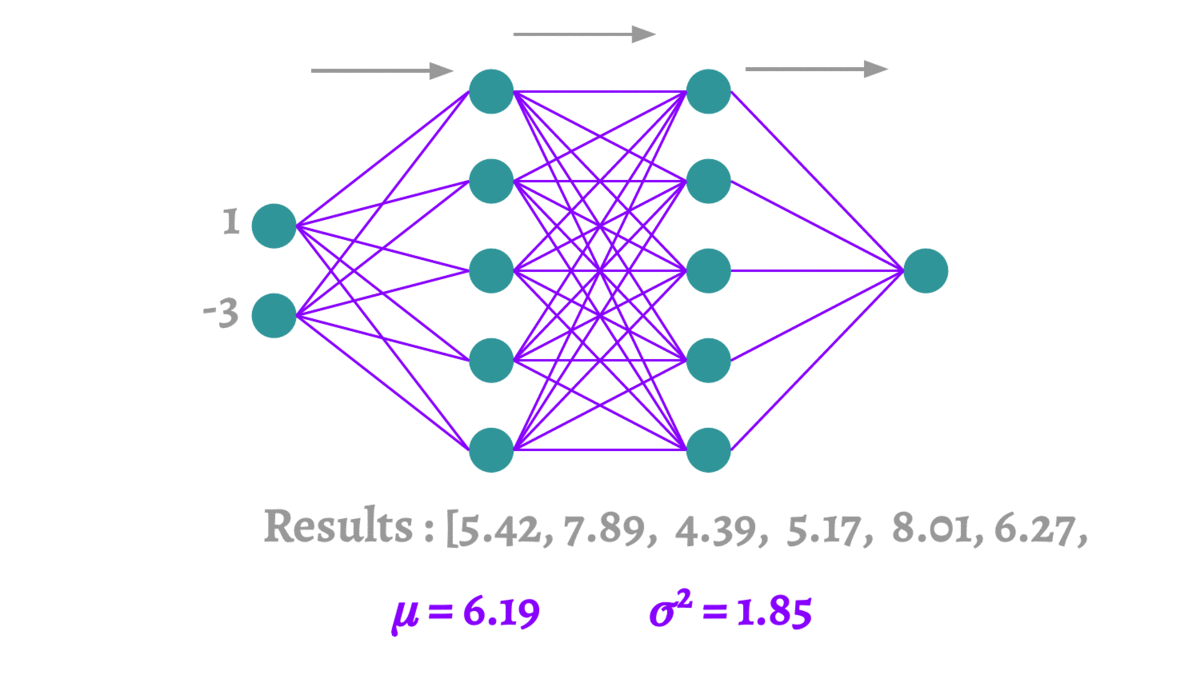
Dropout通过在训练期间随机地“丢弃”（即将输出特征值设置为零）一些层的输出特征来解决过拟合问题。对于每个训练样本（或批次），特定节点以概率p（由实践者选择的超参数）被“关闭”。这种随机性迫使网络学习更加健壮的特征，这些特征与其他神经元的许多不同随机子集一起使用时是有用的。

Dropout如何工作

1. 随机停用：在每个训练阶段，单个节点要么以概率p保持在网络中，要么以概率1-p从网络中被丢弃。
2. 网络变薄：这个过程为每个训练步骤产生一个变薄的网络。每个变薄的网络在数据上进行训练，但丢弃了不同的节点。
3. 预测阶段：在测试阶段不使用dropout。相反，节点的权重会根据概率p缩小，以补偿训练期间激活的节点比训练期间多的事实。

Dropout的好处

• 减少过拟合：通过阻止单元过度协同适应，dropout迫使模型学习更多有助于输出的健壮特征。
• 模型平均效应：Dropout可以被看作是并行训练大量具有不同架构的神经网络的一种方式。在测试期间，它类似于平均这些网络的预测。
• 提高模型性能：通常，使用dropout训练的模型在预测性能方面超过了未使用它的模型。

在神经网络中实现Dropout

Dropout的实现很直接。在大多数深度学习框架中，它涉及添加一个dropout层或为现有层指定一个dropout率。dropout率p是一个可以调整的超参数，通常设置在0.2到0.5之间。

挑战和考虑因素

• 调整Dropout率：找到最佳的dropout率可能很棘手，通常需要交叉验证或其他超参数优化技术。
• 增加训练时间：由于dropout实际上在每个训练步骤训练一个不同的网络，因此可能导致训练时间增加。
• 并非总是有益的：在某些情况下，特别是在小数据集或网络的最后几层中，dropout可能会损害性能。

代码

使用Python在深度学习模型中使用dropout的完整示例涉及多个步骤。我们将创建一个合成数据集，构建一个带有dropout层的神经网络模型，训练模型，并绘制结果以可视化dropout的影响。以下是分步指南：

导入必要的库

我们将使用TensorFlow和Keras来构建神经网络。对于数据操作和绘图，我们将使用NumPy和Matplotlib。

生成合成数据集

我们可以使用sklearn.datasets中的make_classification来创建一个适合二元分类任务的合成数据集。

定义神经网络模型

我们将创建一个简单的神经网络模型并包括dropout层。dropout率是我们可以调整的一个超参数。

编译模型

我们将用优化器、损失函数和用于监控的指标来编译模型。

训练模型

我们将在合成数据集上训练模型，并对其进行验证。这个步骤包括在训练期间使用dropout。

评估模型

训练结束后，我们会在测试集上评估模型的性能。

绘制结果

我们将绘制训练和验证的准确性和损失，以观察dropout的效果。

现在让我们用Python来实现这一点。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.optimizers import Adam
# Generate synthetic dataset
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Define the model
model = Sequential([
    Dense(64, activation='relu', input_shape=(20,)),
    Dropout(0.5),
    Dense(64, activation='relu'),
    Dropout(0.5),
    Dense(1, activation='sigmoid')
])
# Compile the model
model.compile(optimizer=Adam(), loss='binary_crossentropy', metrics=['accuracy'])
# Train the model
history = model.fit(X_train, y_train, epochs=20, batch_size=32, validation_split=0.2)
# Evaluate the model
loss, accuracy = model.evaluate(X_test, y_test)
print(f"Test Accuracy: {accuracy:.4f}")
# Plot training and validation accuracy and loss
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(history.history['accuracy'], label='Train Accuracy')
plt.plot(history.history['val_accuracy'], label='Validation Accuracy')
plt.title('Model Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title('Model Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.tight_layout()
plt.show()

Epoch 1/20
20/20 [==============================] - 4s 49ms/step - loss: 0.7149 - accuracy: 0.5828 - val_loss: 0.5333 - val_accuracy: 0.7875
Epoch 2/20
20/20 [==============================] - 0s 10ms/step - loss: 0.5904 - accuracy: 0.6797 - val_loss: 0.4640 - val_accuracy: 0.8438
Epoch 3/20
20/20 [==============================] - 0s 19ms/step - loss: 0.5856 - accuracy: 0.6953 - val_loss: 0.4172 - val_accuracy: 0.8500
Epoch 4/20
20/20 [==============================] - 0s 15ms/step - loss: 0.4815 - accuracy: 0.7688 - val_loss: 0.3814 - val_accuracy: 0.8375
Epoch 5/20
20/20 [==============================] - 0s 12ms/step - loss: 0.4620 - accuracy: 0.7906 - val_loss: 0.3558 - val_accuracy: 0.8438
Epoch 6/20
20/20 [==============================] - 0s 7ms/step - loss: 0.4748 - accuracy: 0.7797 - val_loss: 0.3370 - val_accuracy: 0.8625
Epoch 7/20
20/20 [==============================] - 0s 13ms/step - loss: 0.4065 - accuracy: 0.8234 - val_loss: 0.3219 - val_accuracy: 0.8625
Epoch 8/20
20/20 [==============================] - 0s 11ms/step - loss: 0.4167 - accuracy: 0.8062 - val_loss: 0.3129 - val_accuracy: 0.8562
Epoch 9/20
20/20 [==============================] - 0s 18ms/step - loss: 0.4277 - accuracy: 0.8359 - val_loss: 0.3083 - val_accuracy: 0.8500
Epoch 10/20
20/20 [==============================] - 0s 8ms/step - loss: 0.3836 - accuracy: 0.8297 - val_loss: 0.3026 - val_accuracy: 0.8687
Epoch 11/20
20/20 [==============================] - 0s 16ms/step - loss: 0.3657 - accuracy: 0.8328 - val_loss: 0.2987 - val_accuracy: 0.8687
Epoch 12/20
20/20 [==============================] - 1s 44ms/step - loss: 0.3892 - accuracy: 0.8422 - val_loss: 0.2957 - val_accuracy: 0.8625
Epoch 13/20
20/20 [==============================] - 0s 7ms/step - loss: 0.3956 - accuracy: 0.8438 - val_loss: 0.2939 - val_accuracy: 0.8625
Epoch 14/20
20/20 [==============================] - 0s 10ms/step - loss: 0.3543 - accuracy: 0.8484 - val_loss: 0.2896 - val_accuracy: 0.8687
Epoch 15/20
20/20 [==============================] - 0s 12ms/step - loss: 0.3675 - accuracy: 0.8562 - val_loss: 0.2857 - val_accuracy: 0.8625
Epoch 16/20
20/20 [==============================] - 0s 16ms/step - loss: 0.3413 - accuracy: 0.8609 - val_loss: 0.2829 - val_accuracy: 0.8625
Epoch 17/20
20/20 [==============================] - 0s 9ms/step - loss: 0.3774 - accuracy: 0.8516 - val_loss: 0.2791 - val_accuracy: 0.8625
Epoch 18/20
20/20 [==============================] - 0s 11ms/step - loss: 0.3712 - accuracy: 0.8266 - val_loss: 0.2808 - val_accuracy: 0.8625
Epoch 19/20
20/20 [==============================] - 0s 6ms/step - loss: 0.3705 - accuracy: 0.8766 - val_loss: 0.2762 - val_accuracy: 0.8625
Epoch 20/20
20/20 [==============================] - 0s 9ms/step - loss: 0.3451 - accuracy: 0.8469 - val_loss: 0.2739 - val_accuracy: 0.8625
7/7 [==============================] - 1s 13ms/step - loss: 0.3579 - accuracy: 0.8500
Test Accuracy: 0.8500

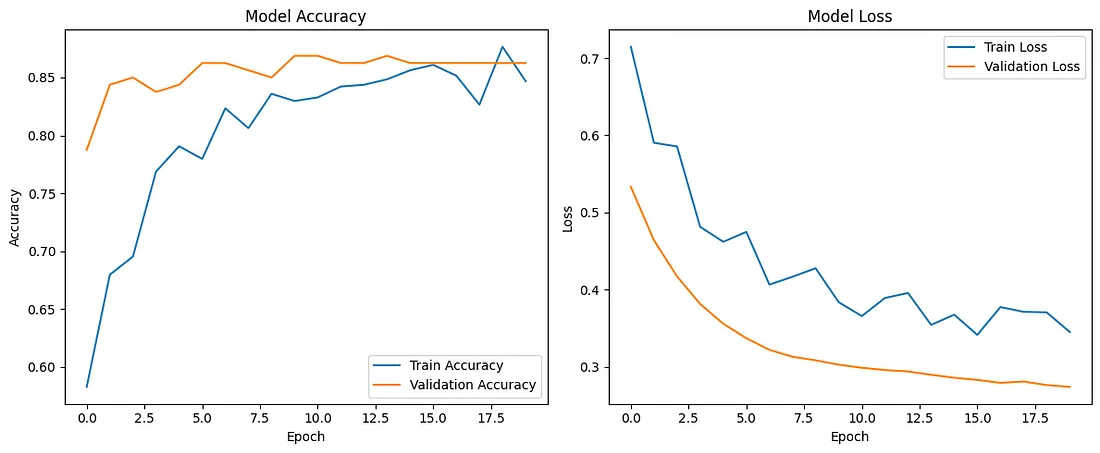
这段代码将创建一个带有中间隔层的两层神经网络。 Dropout（随机失活）率设置为0.5，但你可以尝试不同的值。这些图表将帮助你理解模型在训练集和验证集上的精度和损失随着epochs的变化情况。

结论

Dropout是深度学习中用于对抗过拟合的一种强大而广泛使用的技术。它的简单性和有效性使它成为实践者的宝贵工具。然而，就像任何技术一样，它有其需要考虑的地方，并且在设计和训练神经网络的更广泛策略中应谨慎使用。