向量相似度搜索是从给定向量列表中找出特定嵌入空间内的相似向量。它在各个领域和应用中起着至关重要的作用，因为它能够高效地从大型数据集中检索出相关信息。

向量相似性搜索需要大量的内存资源才能高效搜索，特别是在处理密集型向量数据集时。这就是压缩高维向量以优化内存存储的角色发挥作用的地方。在本文中，我们将讨论

1. 乘积量化（PQ）及其工作原理
2. 倒排文件乘积量化（IVFPQ）索引
3. 使用LanceDB实现IVFPQ

我们还将看到PQ和IVFPQ在内存方面的性能，并介绍使用LanceDB实现IVFPQ索引的过程。

量化是一种用于降维而不丢失重要信息的过程。

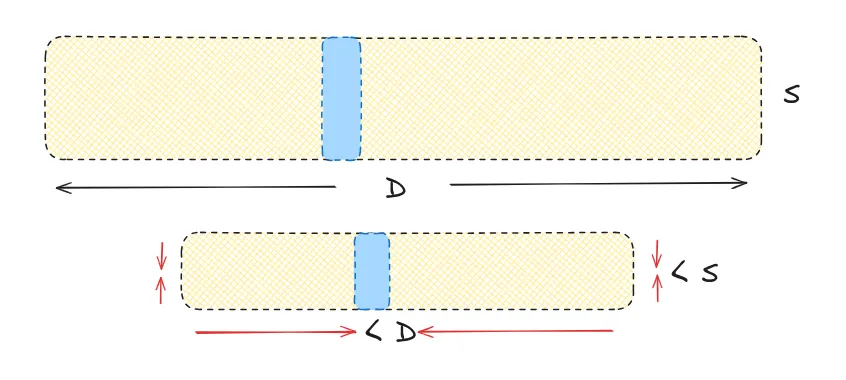
产品量化是如何工作的？

产品量化可以被分解为以下步骤：

1. 将大型高维向量分割成等大小的块，从而创建子向量。
2. 识别每个子向量最近的中心点，将其称为再生值或重构值。
3. 用代表相应中心点的唯一ID替换这些再生值。

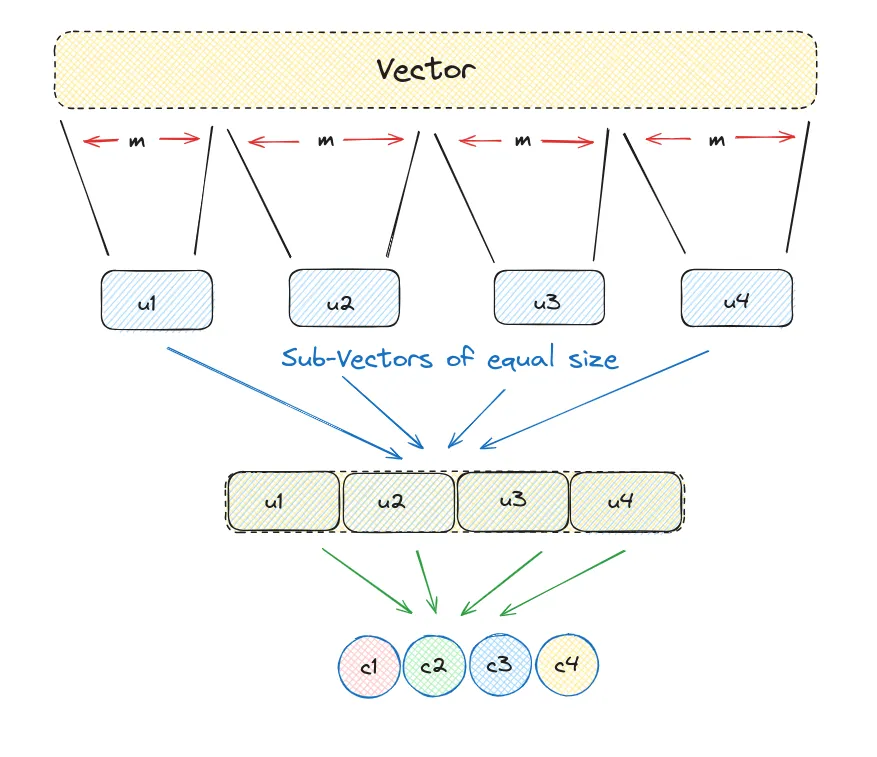
我们来看看在实现中它是怎么工作的，为此我们会创建一个大小为12的随机数组，并且将块大小设置为3。

import random
#consider this as a high dimensional vector
vec = v = [random.randint(1,20)) for i in range(12)]

chunk_count = 4
vector_size = len(vec)
# vector_size must be divisable by chunk_size
assert vector_size % chunk_count == 0
# length of each subvector will be vector_size/ chunk_count
subvector_size = int(vector_size / chunk_count)
# subvectors
sub_vectors = [vec[row: row+subvector_size] for row in range(0, vector_size, subvector_size)]
sub_vectors

输出看起来像这样

[[13, 3, 2], [5, 13, 5], [17, 8, 5], [3, 12, 9]]

这些子向量被替换为一个指定的质心向量，称为生殖值，因为它有助于识别每个子向量。随后，这个质心向量可以被替换为一个独特的ID，该ID对它来说是唯一的。

k = 2**5
assert k % chunk_count == 0
k_ = int(k/chunk_count)
from random import randint
# reproduction values
c = []  
for j in range(chunk_count):
    # each j represents a subvector position
    c_j = []
    for i in range(k_):
        # each i represents a cluster/reproduction value position 
       c_ji = [randint(0, 9) for _ in range(subvector_size)]
       c_j.append(c_ji)  # add cluster centroid to subspace list
    
  # add subspace list of centroids
    c.append(c_j)

#helper function to calculate euclidean distance
def euclidean(v, u):
    distance = sum((x - y) ** 2 for x, y in zip(v, u)) ** .5
    return distance
#helper function to create unique ids
def nearest(c_j, chunk_j):
    distance = 9e9
    for i in range(k_):
        new_dist = euclidean(c_j[i], chunk_j)
        if new_dist < distance:
            nearest_idx = i
            distance = new_dist
    return nearest_idx

现在，让我们看看如何使用最近邻助手函数来获取独特的质心ID。

ids = []
# unique centroid IDs for each subvector
for j in range(chunk_count):
    i = nearest(c[j], sub_vectors[j])
    ids.append(i)
print(ids)

输出显示每个子向量的唯一质心ID。

[5, 6, 7, 7]

当我们利用PQ（乘积量化）处理一个向量时，我们将其划分成多个子向量。这些子向量随后会被处理并且与它们各自子簇中最接近的质心相连，这些质心也称为再现值。

我们不使用质心来保存我们的量化向量，而是用一个独特的质心ID来替代它。每个质心都有它特定的ID，这样我们就能在之后使用这些ID值映射回完整的质心。

quantized = []
for j in range(chunk_count):
    c_ji = c[j][ids[j]]
    quantized.extend(c_ji)
print(quantized)

这是使用质心ID重建的向量。

[9, 9, 2, 5, 7, 6, 8, 3, 5, 2, 9, 4]

在这样做的过程中，我们将一个12维向量压缩为一个由ID表示的4维向量。为了简化起见，我们选择了一个较小的维度，这可能使这项技术的优势不那么立即显而易见。

重要的是要强调，重建后的向量与原始向量不完全相同。这种差异是由所有压缩算法在压缩和重建过程中固有的损失所导致的。

让我们将起始的12维8位整数向量更改为一个更实用的128维32位浮点数向量。通过将其压缩为仅有8个维度的8比特整数向量，我们在性能上达成了很好的平衡。

原始的：128×32 = 4096 量化后的：8×8 = 64

这标示了一个显著的差异——内存减少了64倍。

IVFPQ索引如何帮助加速过程？

在IVFPQ中，一个倒排文件索引（IVF）与产品量化（PQ）相结合，以通过初步的广泛搜索来便捷高效地进行近似最近邻搜索，这种搜索缩小了我们搜索范围内的向量。

之后，我们继续进行我们之前一样的PQ搜索——但是面对的向量数量大大减少。通过最小化我们的搜索范围，预计可以显著提高搜索速度。

使用 LanceDB 只需几行代码即可轻松实现 IVFPQ。

创建 IVF_PQ 索引

import lancedb
import numpy as np
uri = "./lancedb"
db = lancedb.connect(uri)
# Create 10,000 sample vectors
data = [{"vector": row, "item": f"item {i}"}
   for i, row in enumerate(np.random.random((10_000, 1536)).astype('float32'))]
# Add the vectors to a table
tbl = db.create_table("my_vectors", data=data)
# Create and train the index - you need to have enough data in the table for an effective training step
tbl.create_index(num_partitions=256, num_sub_vectors=96)

• metric（默认值：“L2”）：要使用的距离度量。默认情况下，它使用欧几里德距离“L2”。我们还支持“余弦”和“点”距离。
• num_partitions（默认值：256）：索引的分区数。
• num_sub_vectors（默认值：96）：将在乘积量化 (PQ) 期间创建的子向量 (M) 数量。

现在我们来看看这个IVF索引是如何减小向量范围的，倒排文件是一种索引结构，用于将数据库向量映射到它们所在的相应分区。

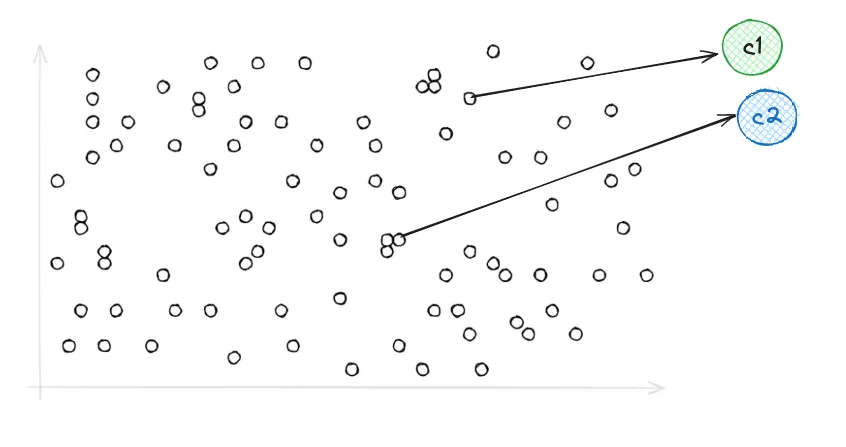
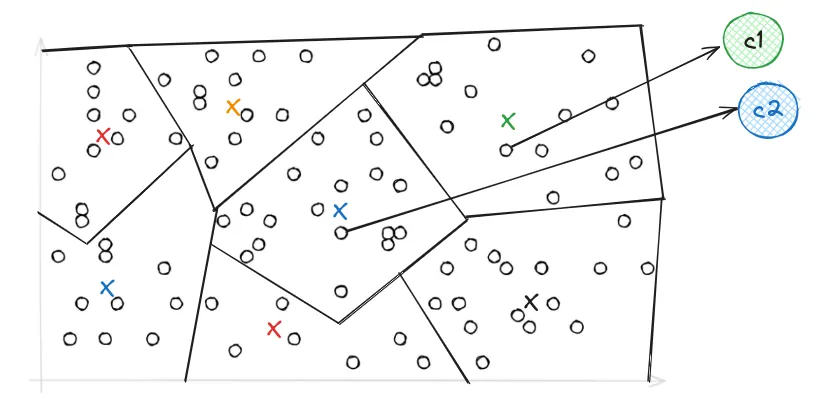
这是 Voronoi 使用 IVF 表示向量的方式，它们简单来说是一组划分，每个划分中包含彼此接近的向量。而在进行搜索时——当我们引入我们的查询向量时，它限制我们的搜索仅在最邻近的单元中进行，因此，搜索速度变得比PQ快得多。

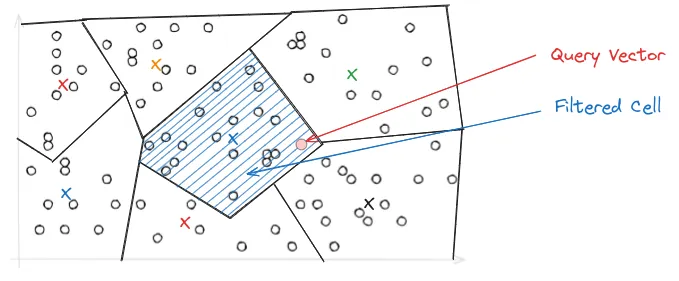
随后，正如我们上面所见，需要应用PQ。

所有这些都可以使用最少的代码通过IVF+PQ指数在LanceDB中应用。

tbl.search(np.random.random((1536))) \
    .limit(2) \
    .nprobes(20) \
    .refine_factor(10) \
    .to_pandas()

• limit（默认值：10）：将返回的结果数
• nprobes（默认值：20）：探针（节）的数量决定向量空间的分布。虽然较高的数字可以提高搜索准确性，但也会导致性能下降。通常，将探针数量 (nprobes) 设置为覆盖数据集的 5-10% 可以有效地以最小的延迟实现高召回率。
• 细化因子（默认值：无）：通过读取额外元素并在内存中重新排列它们来优化结果。
  数字越大，搜索越准确，但速度也越慢。

结论

可以得出结论，产品量化减少了存储高维向量的内存消耗，并且与IVF索引一起，它通过只在最接近的向量中进行搜索，大大加快了过程。