介绍

复数，其特点是同时具有实部与虚部，它们在推动深度学习算法和架构的发展方面的潜力日益受到认可。在本文中，我将探讨如何在深度学习中使用复数，它们的好处、挑战以及潜在的未来应用。

深度学习中复数简介

复数以a + bi的形式表示，其中a是实部，bi是虚部，i是-1的平方根。在深度学习中，这些数字提供了一种独特的方式来表示和处理信息。与仅依赖实数的传统方法不同，复值神经网络（CVNNs）可以直接处理和学习复数数据。

复数在深度学习中的优势

1. 增强的数据表示能力：复数允许更细致的数据表示。例如，在信号处理中，它们可以同时表示振幅和相位信息，与实数相比提供了更丰富的数据表示。
2. 提高学习动态性：复平面的几何性质可能导致神经网络中更好的学习动态。例如，能够在复平面中旋转和缩放向量可以在训练期间更灵活地调整神经元权重。
3. 自然契合某些应用：在量子计算、电磁学和信号处理等领域，数据本质上就是复值的。CVNN天然适用于这些领域，有可能提高模型性能和效率。

面临的挑战和考虑事项

1. 增加的计算复杂性：与实数相比，处理复数通常需要更多的计算资源，因为操作要在实部和虚部上进行。
2. 训练和优化：现有的训练算法和优化技术主要是为实值网络设计的。将这些适配到复值网络可能是具有挑战性的，需要新的方法和途径。
3. 可解释性和可视化：复数的多维特性可能会使得可视化和解释模型变得更加困难，而这对于理解和调试神经网络至关重要。

应用和未来方向

1. 信号处理：CVNNs已在应用中显示出前景，例如在无线通信中，它们可以有效地处理复信号数据。
2. 量子计算：随着量子计算的发展，复数在这一领域的相关性可能为深度学习模型与量子算法的交互提供新的机会。
3. 图像和音频处理：复数可以有效地表示图像数据（例如在频域表示中）和音频信号，为这些领域提供了新的途径。
4. 探索新架构：研究利用复数属性的新神经网络架构可能会导致深度学习能力的突破。

代码

使用Python在深度学习中使用复数的完整示例需要几个步骤。我们将创建一个合成数据集，设计一个复值神经网络（CVNN），在数据集上训练它，然后绘制结果。在此示例中，我将使用NumPy等Python库进行数据操作，以及TensorFlow或PyTorch构建神经网络。

步骤1：安装必要的库

确保你安装了TensorFlow或PyTorch、NumPy和Matplotlib。你可以使用pip安装它们：

pip install tensorflow numpy matplotlib

让我们一步一步地实施这个：

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.models import Model
import matplotlib.pyplot as plt
def generate_synthetic_data(num_samples=1000):
    # Generate random complex numbers
    real_parts = np.random.uniform(-1, 1, num_samples)
    imaginary_parts = np.random.uniform(-1, 1, num_samples)
    complex_numbers = real_parts + 1j * imaginary_parts
    # Labels: 1 if the real part is greater than 0.5, else 0
    labels = (real_parts > 0.5).astype(int)
    return complex_numbers, labels
X, y = generate_synthetic_data()
class ComplexValuedNN(Model):
    def __init__(self):
        super(ComplexValuedNN, self).__init__()
        self.flatten = Flatten()
        self.d1 = Dense(128, activation='relu')
        self.d2 = Dense(2, activation='softmax')  # Output layer for 2 classes
    def call(self, x):
        x = self.flatten(x)
        x = self.d1(x)
        return self.d2(x)
model = ComplexValuedNN()
model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])
# Convert complex numbers to two channels for real and imaginary parts
X_train = np.stack((X.real, X.imag), axis=-1)
model.fit(X_train, y, epochs=10)
history = model.fit(X_train, y, epochs=10, validation_split=0.2)
# Plot training & validation accuracy values
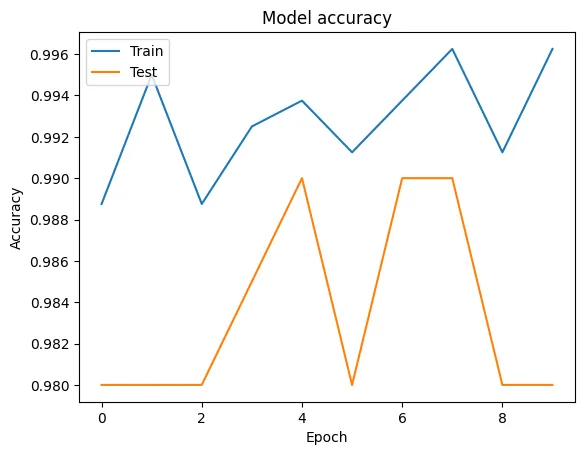
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# Plot training & validation loss values
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()

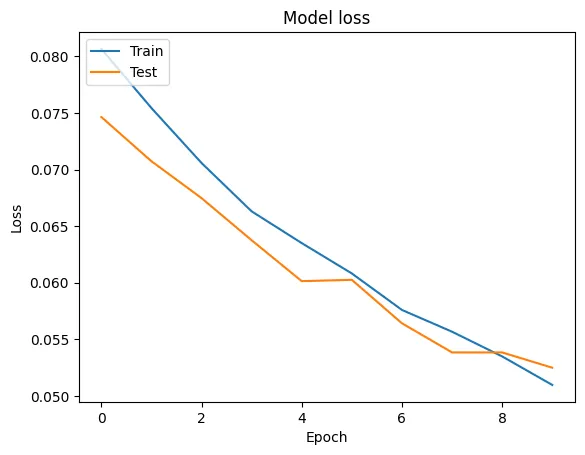
这是一个开始的基本框架。此外，在神经网络中处理复数可能更加复杂，这取决于具体任务和数据特征。

结论

将复数整合到深度学习中，呈现出一个令人着迷的探索领域。尽管在计算要求和适应现有方法论方面存在挑战，但在数据表示、学习动态和特定应用的性能方面潜在的好处是显著的。随着研究的进展，我们可以期待看到复数在深度学习中的更多创新应用，可能会彻底改变我们处理和学习复杂数据的方式。