微调大型预训练模型在计算上具有挑战性，通常涉及调整数百万个参数。这种传统的微调方法虽然有效，但需要大量的计算资源和时间，成为将这些模型适配到特定任务的瓶颈。LoRA通过在微调过程中分解更新矩阵，为这个问题提供了一种有效的解决方案。为了学习LoRA，让我们首先回顾传统的微调。

（ΔW）的分解

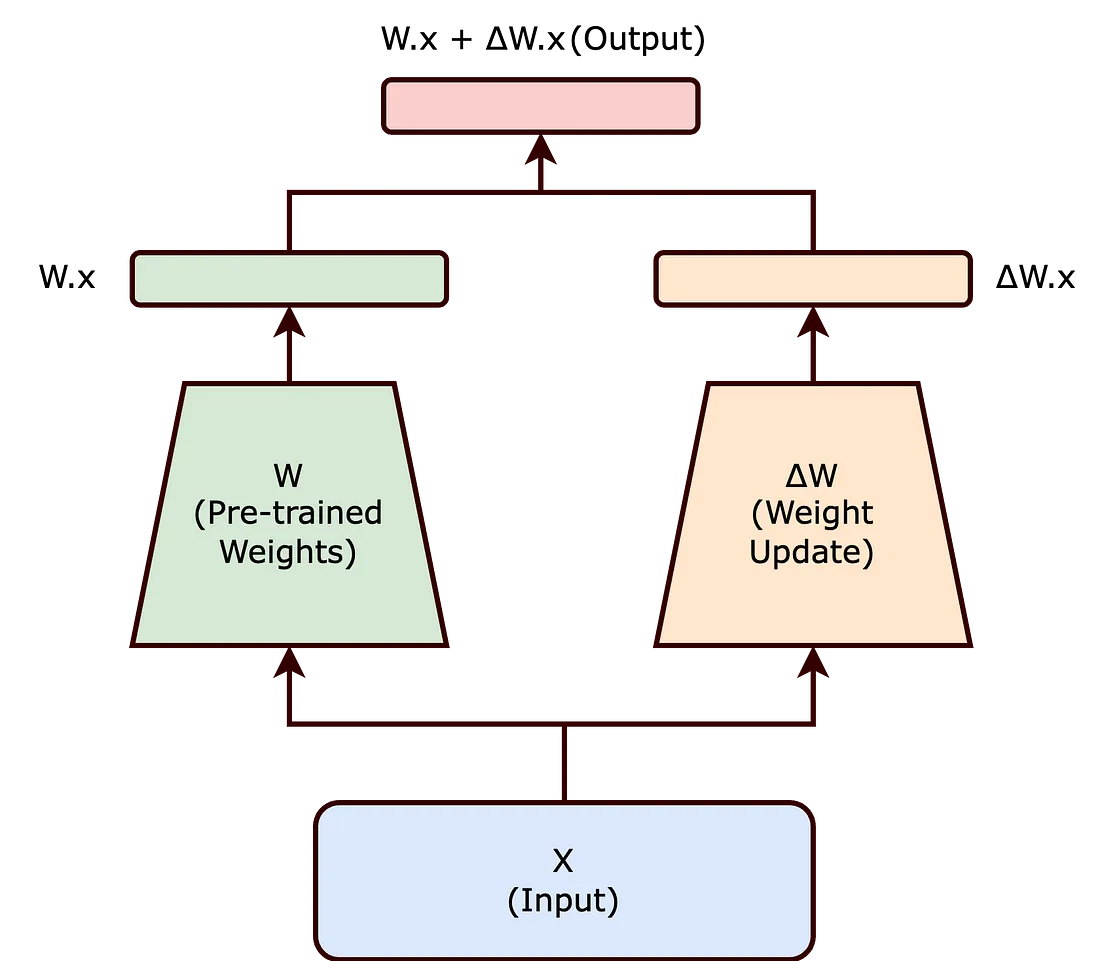
在传统的微调中，我们修改预训练神经网络的权重以适应新任务。这种调整涉及改变网络的原始权重矩阵（W）。在微调期间对（W）所做的更改统称为（ΔW），这样更新后的权重可以表示为（W + ΔW）。

现在，LoRA方法不是直接修改（W），而是寻求分解（ΔW）。这种分解是减少微调大模型所关联的计算开销的关键步骤。

内在等级假设

内在等级假设认为，对神经网络的重大改变可以通过较低维度的表示来捕获。本质上，它认为并非所有的 ( Δ W ) 元素都同等重要；相反，这些变化中的一个更小的子集可以有效地封装必要的调整。

引入矩阵 ( A ) 和 ( B )

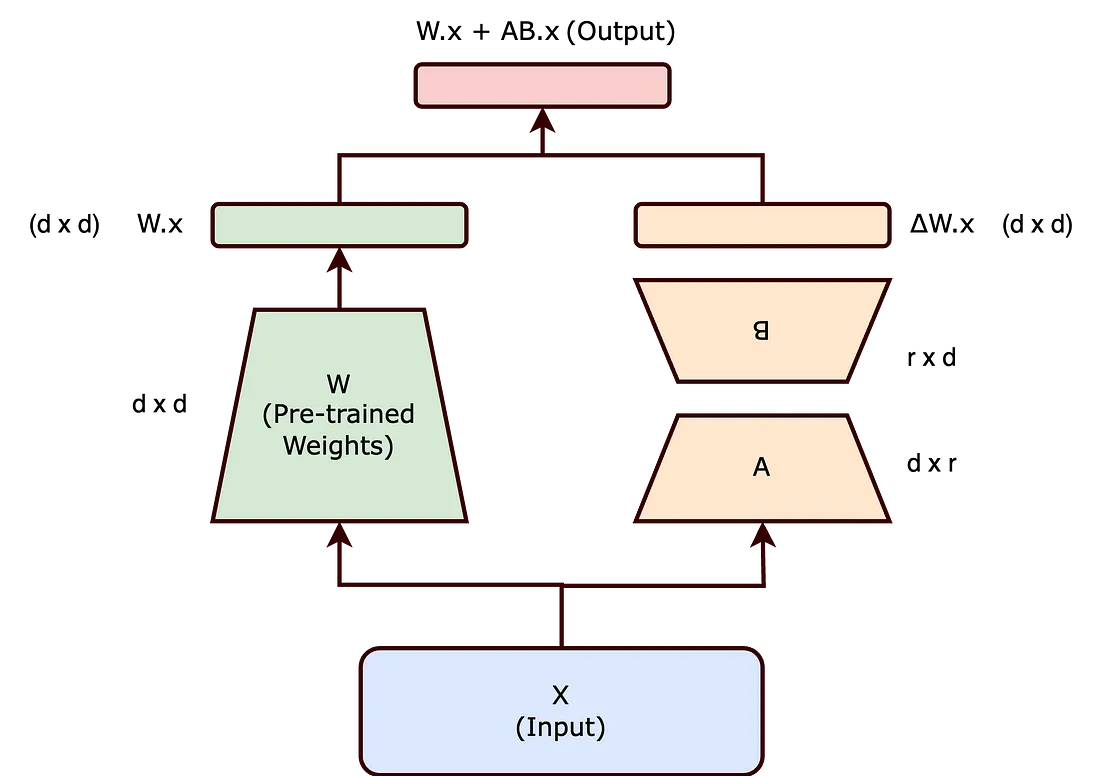
基于这个假设，LoRA 提出将 ( Δ W ) 表示为两个较小矩阵 ( A ) 和 ( B ) 的乘积，这两个矩阵的等级较低。因此，更新后的权重矩阵 ( W’ ) 变为：

[ W’ = W + BA ]

在这个方程中，( W ) 保持冻结（即，在训练期间不更新）。矩阵 ( B ) 和 ( A ) 的维度较低，它们的乘积 ( BA ) 代表了 ( Δ W ) 的低阶近似。

降低秩对可训练参数的影响

通过选择矩阵（A）和（B）具有较低的秩（r），可显著减少训练参数的数量。举例来说，如果（W）是一个（d x d）矩阵，传统上，更新（W）将涉及（d²）个参数。然而，如果（B）和（A）的大小分别是（d x r）和（r x d），那么参数总数减少到（2dr），当（r << d）时，这个数字要小得多。

通过低秩适应（ LoRA）方法实现的可训练参数数量减少，在微调大规模神经网络时带来了几个显著的好处：

1. 减少内存占用：LoRA通过降低需要更新的参数数量来减少内存需求，有助于管理庞大的模型。
2. 加快训练和适应：通过简化计算需求，LoRA加速了大模型针对新任务的训练和微调。
3. 适用于小型硬件：LoRA较少的参数计数使得在较不强大的硬件上微调大型模型成为可能，如中等GPU或CPU。
4. 扩展到更大的模型：LoRA促进了AI模型的扩展，而无需相应增加计算资源，使得管理不断增长的模型大小更加切实可行。

在LoRA的背景下，秩的概念在确定适应过程的效率和有效性方面起着关键作用。值得注意的是，论文强调矩阵A和B的秩可以非常低，有时低至一。

虽然LoRA论文主要展示了自然语言处理（NLP）领域内的实验，但低秩适应的基本方法具有广泛的适用性，并且可以有效地用于训练不同领域的各种类型的神经网络。

结论

LoRA将（ΔW）分解为低秩矩阵的乘积的方法，有效地平衡了将大型预训练模型适应新任务的需求与计算效率的维持。内在的秩概念是这种平衡的关键，确保在参数数量显著减少的情况下保留了模型的学习能力的本质。